Funzioni in R
Ho risolto il seguente quesito, ma spero di aver fatto bene, ecco quì:
Per il primo quesito.
a) $ [a,b ) $
b) $ (-oo, a ] $
c) $ (a, b ]uu[c,d] $
d) $ [a,+oo ) $
e) $ (a,b) uu [c,+oo) $
f) $ [a,b ] $
Per il secondo quesito.
a) Penso si riferisca ad un intorno circolare, ma come posso esprimerlo?
Per il primo quesito.
a) $ [a,b ) $
b) $ (-oo, a ] $
c) $ (a, b ]uu[c,d] $
d) $ [a,+oo ) $
e) $ (a,b) uu [c,+oo) $
f) $ [a,b ] $
Per il secondo quesito.
a) Penso si riferisca ad un intorno circolare, ma come posso esprimerlo?
Risposte
Sto risolvendo i seguenti esercizi aventi la seguente traccia:
Date le funzioni $ f(x) = 2^(x-2) $ e $ g(x) = 2^(|x|-2) $ , calcolare:
$ f(-1) $
Ma come bisogna comportarsi quando si ha quel valore assoluto in $ g(x) $



Date le funzioni $ f(x) = 2^(x-2) $ e $ g(x) = 2^(|x|-2) $ , calcolare:
$ f(-1) $
Ma come bisogna comportarsi quando si ha quel valore assoluto in $ g(x) $
$|x|={\(x, if x>=0), (-x, if x<0):}$, nel tuo caso $-1$ è negativo, quindi per togliere il valore assoluto lo devi cambiare di segno, $|-1|= -(-1) = 1$
$ f(-1) =2^(-1-2)=2^(-3)=1/2^3=1/8$
$ g(-1) = 2^(|-1|-2)=2^(1-2)=2^(-1)=1/2 $
$ f(-1) =2^(-1-2)=2^(-3)=1/2^3=1/8$
$ g(-1) = 2^(|-1|-2)=2^(1-2)=2^(-1)=1/2 $
Se mi viene chiesto di dire se le seguenti coppie di funzioni $ f(x) $ e $ g(x) $ sono uguali, come posso rispondere?
$ f(x) = sqrt(x^2) $ e uguale a $ g(x) = |x| $

A me viene di dire che è vero, sono uguali in quanto in $ mathbb(R) $ , la seguente $ f(x) = sqrt(x^2) $ è sempre positivo, perchè un quadrato è sempre positivo!
Ma non saprei spiegarlo diversamente
$ f(x) = sqrt(x^2) $ e uguale a $ g(x) = |x| $
A me viene di dire che è vero, sono uguali in quanto in $ mathbb(R) $ , la seguente $ f(x) = sqrt(x^2) $ è sempre positivo, perchè un quadrato è sempre positivo!
Ma non saprei spiegarlo diversamente
"Bad90":
Se mi viene chiesto di dire se le seguenti coppie di funzioni $ f(x) $ e $ g(x) $ sono uguali, come posso rispondere?
$ f(x) = sqrt(x^2) $ e uguale a $ g(x) = |x| $

A me viene di dire che è vero, sono uguali in quanto in $ mathbb(R) $ , la seguente $ f(x) = sqrt(x^2) $ è sempre positivo, perchè un quadrato è sempre positivo!
Ma non saprei spiegarlo diversamente
La radice quadrata di un numero reale non negativo (e $x^2>=0$) è sempre un numero reale non negativo, quindi \(\sqrt{x^2} \neq x\) e \(\sqrt{x^2} \neq \pm x\) ma $\sqrt{x^2}=|x|$.
Perché questo? Beh, è probabile che a te venga da dire \(\sqrt{4}=\pm 2\), vero? Dopotutto, $2^2=(-2)^2=4$... Ma questa non sarebbe una funzione! Infatti, assocerebbe ad un elemento del suo dominio \(\mathbb{R}^+\) (in questo caso $4$) due valori di un eventuale codominio (in questo caso $2$ e $-2$), e ciò contraddice la definizione di funzione. Il problema si risolve prendendo in considerazione, per convenzione, soltanto la soluzione positiva, dunque: $\sqrt{x^2}=|x|$. Adesso sì che siamo difronte ad una funzione! Infatti, in questo modo, abbiamo $\sqrt{4}=2=|2|=|-2|$.
Spero di essermi fatto capire.
E si! Prendendo in considerazione solo la condizione di positivita' del quadrato, allora si he diventa una funzione! 
Aggiungo qualcosa a quanto hai detto e correggimi se sto sbagliando:
Si puo' dire che in una funzione del tipo $y = f(x)$, non ci possono essere due punti appartenenti alla stessa retta, insomma: Una funzione del tipo $y = f(x)$, sarà tale solo se a tale retta, apparterrà solo un punto, ma se si avranno più di un punto, allora non sarà una funzione, infatti l'immagine di ogni $x$ del dominio, deve essere unica!
Penso che questo centri qualcosa, giusto???

Aggiungo qualcosa a quanto hai detto e correggimi se sto sbagliando:
Si puo' dire che in una funzione del tipo $y = f(x)$, non ci possono essere due punti appartenenti alla stessa retta, insomma: Una funzione del tipo $y = f(x)$, sarà tale solo se a tale retta, apparterrà solo un punto, ma se si avranno più di un punto, allora non sarà una funzione, infatti l'immagine di ogni $x$ del dominio, deve essere unica!
Penso che questo centri qualcosa, giusto???
Non sto capendo la traccia del seguente:
Determinare un sottoinsieme A dell'insieme di definizione della funzione $ y = tg x$, in modo che essa risulti biiettiva da $ A $ in $ R$
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Determinare un sottoinsieme A dell'insieme di definizione della funzione $ y = tg x$, in modo che essa risulti biiettiva da $ A $ in $ R$
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
"Bad90":
E si! Prendendo in considerazione solo la condizione di positivita' del quadrato, allora si he diventa una funzione!
Aggiungo qualcosa a quanto hai detto e correggimi se sto sbagliando:
Si puo' dire che in una funzione del tipo $y = f(x)$, non ci possono essere due punti appartenenti alla stessa retta, insomma: Una funzione del tipo $y = f(x)$, sarà tale solo se a tale retta, apparterrà solo un punto, ma se si avranno più di un punto, allora non sarà una funzione, infatti l'immagine di ogni $x$ del dominio, deve essere unica!
Penso che questo centri qualcosa, giusto???
Se con "retta" intendi "retta verticale (parallela all'asse $y$)" allora sì. Questa è una cosa che esiste, e si chiama test delle parallele.
Analogamente, usando rette parallele l'asse $x$ si fa il test di invertibilità.
"giuliofis":
Se con "retta" intendi "retta verticale (parallela all'asse $y$)" allora sì. Questa è una cosa che esiste, e si chiama test delle parallele.
Analogamente, usando rette parallele l'asse $x$ si fa il test di invertibilità.
Si intendo quella

"Bad90":
Non sto capendo la traccia del seguente:
Determinare un sottoinsieme A dell'insieme di definizione della funzione $ y = tg x$, in modo che essa risulti biiettiva da $ A $ in $ R$
HELPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Biettiva significa suriettiva e iniettiva. Tu vuoi, quindi, che ad ogni elemento del dominio corrisponda uno e un solo elemento del codominio [size=85](definizione di funzione)[/size] ed anche che ad ogni elemento del codominio [size=85](suriettiva)[/size] corrisponda uno e un solo elemento del dominio [size=85](iniettiva)[/size]. Deve esserci, cioè, detto in modo poetico, una corrispondenza 1:1.
Ricordando che il grafico di \(f(x)=\tan{x}\) è
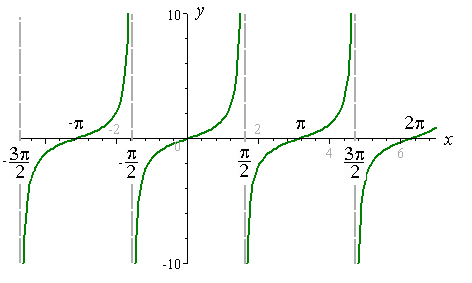
e ricordando il test delle parallele per l'invertibilità di cui ti ho parlato nel precedente post riesci ad intravedere qualcosa?
"giuliofis":
e ricordando il test delle parallele per l'invertibilità di cui ti ho parlato nel precedente post riesci ad intravedere qualcosa?
No, non riesco a intravedere .......
"Bad90":
[quote="giuliofis"]
e ricordando il test delle parallele per l'invertibilità di cui ti ho parlato nel precedente post riesci ad intravedere qualcosa?
No, non riesco a intravedere .......
Allora prova a dirmi in quale sottoinsieme del suo dominio la funzione \(\tan{x}\) ti sembra iniettiva (e non necessariamente suriettiva) e in quale ti sembra suriettiva (e non necessariamente iniettiva).
Insomma, prova a scomporre il problema.
Allora, ricordando il test della retta, in questo caso parallela all'asse $y$, la funzione $ tg x $, sarà sempre biiettiva, tranne quando ci saranno due punti in comune, ma a che angolo si avranno due punti in comune 
"Bad90":
Allora, ricordando il test della retta, in questo caso parallela all'asse $y$, la funzione $ tg x $, sarà sempre biiettiva, tranne quando ci saranno due punti in comune, ma a che angolo si avranno due punti in comune
Con il test delle parallele all'asse $y$ trovi solo che \(\tan{x}\) è una funzione... Devi fare quello delle parallele all'asse $x$ per vedere se (in questo caso: dove) la funzione è iniettiva.
"giuliofis":
[quote="Bad90"]Allora, ricordando il test della retta, in questo caso parallela all'asse $y$, la funzione $ tg x $, sarà sempre biiettiva, tranne quando ci saranno due punti in comune, ma a che angolo si avranno due punti in comune
Con il test delle parallele all'asse $y$ trovi solo che \(\tan{x}\) è una funzione... Devi fare quello delle parallele all'asse $x$ per vedere se (in questo caso: dove) la funzione è iniettiva.[/quote]
Ma la funzione tangente, è non iniettiva, come può essere biiettiva?
Esempi di funzioni iniettive sono la retta, la radice quadrata, il logaritmo, l’esponenziale; esempi di funzioni
non iniettive sono la parabola, il seno, il coseno, la tangente, il ramo superiore di una circonferenza.
"Bad90":
Ma la funzione tangente, è non iniettiva, come può essere biiettiva?
Infatti sei tu che devi restringere il dominio della tangente affinché lo sia! Devi trovare un sottoinsieme del dominio della tangente affinché la funzione, considerata solo lì dentro (in termini tecnici: ristretta), sia iniettiva.
"giuliofis":
[quote="Bad90"]Ma la funzione tangente, è non iniettiva, come può essere biiettiva?
Infatti sei tu che devi restringere il dominio della tangente affinché lo sia! Devi trovare un sottoinsieme del dominio della tangente affinché la funzione, considerata solo lì dentro (in termini tecnici: ristretta), sia iniettiva.[/quote]
E allora non sto capendo come fare
"Bad90":
[quote="giuliofis"][quote="Bad90"]Ma la funzione tangente, è non iniettiva, come può essere biiettiva?
Infatti sei tu che devi restringere il dominio della tangente affinché lo sia! Devi trovare un sottoinsieme del dominio della tangente affinché la funzione, considerata solo lì dentro (in termini tecnici: ristretta), sia iniettiva.[/quote]
E allora non sto capendo come fare
Prendi un sottoinsieme del dominio della funzione.
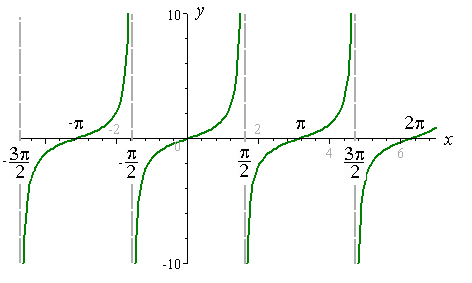
Ad esempio:
1. $[-\pi,-\pi/2)uu(-\pi/2,0]$. È suriettiva? Sì. È iniettiva? Dimmelo tu. Ricorda che $\tan(-\pi)=...$ e $\tan(0)=...$
2. $[-\pi/2,\pi/2]$. È suriettiva? Sì. È iniettiva? Dimmelo tu.
"giuliofis":
Prendi un sottoinsieme del dominio della funzione.
Ad esempio:
1. $[-\pi,-\pi/2)uu(-\pi/2,0]$. È iniettiva? Sì. È suriettiva? Dimmelo tu. Ricorda che $\tan(-\pi)=...$ e $\tan(0)=...$
2. $[-\pi/2,\pi/2]$. È iniettiva? Sì. È suriettiva? Dimmelo tu.
Allora, una funzione è iniettiva quando ad un elemento è associata una sola immagine, mentre la funzione non è iniettiva quando a due elementi es.$ 2$ e $-2$ è associata la stessa immagine, ecco qui un esempio $ f (2) = 1 $; $ f (-2) = 1 $.
Va bene fin quì?
Per dire se una funzione sia surriettiva, dovrei trovare degli elementi di A che risultano non essere immagine di qualche elemento di B
Ma in questo caso, non sto capendo ciò che hai scritto negli esempi
Insomma, come faccio a dire se è surriettiva
1. $[-\pi,-\pi/2)uu(-\pi/2,0]$. È iniettiva? Sì. È suriettiva? Dimmelo tu. Ricorda che $\tan(-\pi)=...$ e $\tan(0)=...$
2. $[-\pi/2,\pi/2]$. È iniettiva? Sì. È suriettiva? Dimmelo tu.
Qui scusami ma avevo sbagliato io a scrivere, ho invertito iniettiva con suriettiva! Perdonami...
Dovevo scriverti:
1. $[-\pi,-\pi/2)uu(-\pi/2,0]$. È suriettiva? Sì. È iniettiva? Dimmelo tu. Ricorda che $\tan(-\pi)=...$ e $\tan(0)=...$
2. $[-\pi/2,\pi/2]$. È suriettiva? Sì. È iniettiva? Dimmelo tu.
Ma in questo caso, non sto capendo ciò che hai scritto negli esempi
Consideriamo il caso (1). Fai finta che la funzione sia definita solo in $[-\pi,-\pi/2)uu(-\pi/2,0]$ e non da altre parti, fai finta che $[-\pi,-\pi/2)uu(-\pi/2,0]$ sia il "dominio" della funzione. Questo procedimento si chiama restrizione. Lì dentro, la funzione è suriettiva. È anche iniettiva?
Stessa domanda per il caso (2).
"giuliofis":
Ma in questo caso, non sto capendo ciò che hai scritto negli esempi
Consideriamo il caso (1). Fai finta che la funzione sia definita solo in $[-\pi,-\pi/2)uu(-\pi/2,0]$ e non da altre parti, fai finta che $[-\pi,-\pi/2)uu(-\pi/2,0]$ sia il "dominio" della funzione. Questo procedimento si chiama restrizione. Lì dentro, la funzione è suriettiva. È anche iniettiva?
Stessa domanda per il caso (2).
Non è assolutamente iniettiva in questi intervalli, perché a due elementi è associata la stessa immagine!
Intendo $ -pi $ e $ 0 $, danno lo stesso risultato







 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo