Funzioni in R
Ho risolto il seguente quesito, ma spero di aver fatto bene, ecco quì:
Per il primo quesito.
a) $ [a,b ) $
b) $ (-oo, a ] $
c) $ (a, b ]uu[c,d] $
d) $ [a,+oo ) $
e) $ (a,b) uu [c,+oo) $
f) $ [a,b ] $
Per il secondo quesito.
a) Penso si riferisca ad un intorno circolare, ma come posso esprimerlo?
Per il primo quesito.
a) $ [a,b ) $
b) $ (-oo, a ] $
c) $ (a, b ]uu[c,d] $
d) $ [a,+oo ) $
e) $ (a,b) uu [c,+oo) $
f) $ [a,b ] $
Per il secondo quesito.
a) Penso si riferisca ad un intorno circolare, ma come posso esprimerlo?
Risposte
Il caso (1) non è un intervallo, è un'unione di intervalli. Sei sicuro che in $[-\pi/2,\pi/2]$ (un intervallo, questo sì) non sia iniettiva? Come mai ne sei così convinto?
"giuliofis":
Il caso (1) non è un intervallo, è un'unione di intervalli. Sei sicuro che in $[-\pi/2,\pi/2]$ (un intervallo, questo sì) non sia iniettiva? Come mai ne sei così convinto?
Non è che hai sbagliato di nuovo a scrivere nel messaggio precedente
Non ho visto che prima hai scritto $[-\pi/2,\pi/2]$, comunque perdonami, ma non ti sto proprio capendo
Io penso che non è assolutamente iniettiva in $[-\pi/2,\pi/2]$, perché a due elementi è associata la stessa immagine!
"Bad90":
Non è che hai sbagliato di nuovo a scrivere nel messaggio precedente
No,
2. $[-\pi/2,\pi/2]$
l'ho indicato con il (2) questo.
Io penso che non è assolutamente iniettiva in $[-\pi/2,\pi/2]$, perché a due elementi è associata la stessa immagine!
Non è associata la stessa immagine a nessun punto di $[-\pi/2,\pi/2]$. Perché dici questo?
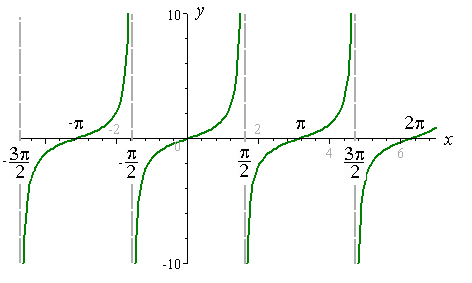
In $[-\pi/2,\pi/2]$ è sia suriettiva che iniettiva, dunque biettiva. Infatti, è proprio in questo intervallo che la funzione risulta invertibile, ed infatti la funzione \(\arctan{x}\) ha come dominio $RR$ e come codominio $[-\pi/2,\pi/2]$.
Accipicchia, stai riuscendo a farmi ragionare 
Allora, in questa circostanza $[-\pi/2,\pi/2]$, si ha che è biiettiva, perchè invece in tutti gli altri casi non lo è

Allora, in questa circostanza $[-\pi/2,\pi/2]$, si ha che è biiettiva, perchè invece in tutti gli altri casi non lo è
"Bad90":
Accipicchia, stai riuscendo a farmi ragionare
Allora, in questa circostanza $[-\pi/2,\pi/2]$, si ha che è biiettiva, perchè invece in tutti gli altri casi non lo è
Beh, lo è anche in $[\pi/2,(3/2)\pi]$... Sono infiniti tali sottoinsiemi, è periodica. Però se devi sceglierne uno, io sceglierei il più semplice!
In quello che ho indicato con (1), ad esempio, invece, vale $\tan(-\pi)=\tan(0)=0$, quindi non è iniettiva e dunque nemmeno biettiva.
"giuliofis":
In quello che ho indicato con (1), ad esempio, invece, vale $\tan(-\pi)=\tan(0)=0$, quindi non è iniettiva e dunque nemmeno biettiva.
Ecco perchè io ho detto che non era biiettiva, per $\tan(-\pi)=\tan(0)=0$ e poi pensavo che valeva sempre questa situazione
Qui si può utilizzare la verifica della retta.......
Quindi vediamo se ho capito un po alcuni concetti, grazie a questo esempio della $ tgx $ .... 
La funzione si può dire che è surriettiva perchè centra con il domino della funzione che è sempre $ mathbb(R) $ , giusto
Il perchè è iniettiva, l'ho compreso perfettamente!
La funzione si può dire che è surriettiva perchè centra con il domino della funzione che è sempre $ mathbb(R) $ , giusto
Il perchè è iniettiva, l'ho compreso perfettamente!

"Bad90":
perchè centra con il domino della funzione che è sempre $ mathbb(R) $
Che vuol dire? Proprio in italiano... E poi $RR$ è il codominio, non il dominio...
"giuliofis":
E poi $RR$ è il codominio, non il dominio...
La funzione si dice suriettiva perché gli elementi di B, sono immagine di almeno un elemento di A.
Lasciamo stare che sto solo facendo un casino



Servirebbero altri esempi per comprendere meglio questa storia Suriettiva
Ecco quì un esempio che ho compreso perfettamente:
Vedi? Con questi esempi riesco a capire il concetto, ma quando si parla di dominio, codominio e ....., faccio fatica!
"Bad90":
ma quando si parla di dominio, codominio e ....., faccio fatica!
Devi abituarti, all'esame te lo chiederanno così.
Vedi quanto è bello e semplice da capire questo esempio:
E ancora questo, da notare la semplicità di comprensione:
E ancora questo, da notare la semplicità di comprensione:
"giuliofis":
[quote="Bad90"]ma quando si parla di dominio, codominio e ....., faccio fatica!
Devi abituarti, all'esame te lo chiederanno così.[/quote]
Potresti farmi un esempio di codominio
Comunque in merito alla funzione tangente ho trovato ciò che mi hai detto prima, ecco quì:
"Bad90":
[quote="giuliofis"][quote="Bad90"]ma quando si parla di dominio, codominio e ....., faccio fatica!
Devi abituarti, all'esame te lo chiederanno così.[/quote]
Potresti farmi un esempio di codominio
Sia $f:A -> B$. $A$ è il dominio della funzione $f$, mentre $B$ il codominio.
Es. $F:[-1,1] -> RR$ con $F(x)=2x$. $[-1,1]$ è il dominio, $RR$ è il codominio, mentre $[-2,2]$ è l'immagine.
Leggi qui se vuoi altre informazioni.
"Bad90":
Comunque in merito alla funzione tangente ho trovato ciò che mi hai detto prima, ecco quì:
 Il che ti fa notare una mia imprecisione nella notazione! Ho usato $[]$ ma avrei dovuto usare $()$.
Il che ti fa notare una mia imprecisione nella notazione! Ho usato $[]$ ma avrei dovuto usare $()$.
"giuliofis":
In $[-\pi/2,\pi/2]$ è sia suriettiva che iniettiva, dunque biettiva. Infatti, è proprio in questo intervallo che la funzione risulta invertibile, ed infatti la funzione \(\arctan{x}\) ha come dominio $RR$ e come codominio $[-\pi/2,\pi/2]$.
Scusami, ma si può fare la verifica del grafico della retta?
Perchè non mi è tanto chiaro graficamente questa biiettività

Mettiamo un po da parte il gergo troppo rigorosamente matematico, conviene utilizzare un linguaggio che è più terra terra per un poveraccio come me
Ho trovato anche questo:
Funzioni iniettive e suriettive?
Per esempio dato l'insieme A: {-1;5;7;11} e B: {0;4;7;9;14} definire una funzione iniettiva e una non iniettiva
Una funzione iniettiva f è tale che per ogni x e yche appartengono al tuo dominio si ha che f(x)=f(y) se e solo se x=y
In parole povere significa che la tua funzione deve associare ad ogni elemento un valore ma mai associare lo stesso valore a due elementi
Per esempio da A a B una funzione iniettiva può essere
f:A->B tale che
f(-1)=0
f(5)=9
f(7)=4
f(11)=7
Ovviamente puoi cambiare come vuoi le tue immagini basta che ti ricordi che per essere iniettiva non associ mai a due elementi lo stesso valore
una funzione non iniettiva è:
f(-1)=0
f(5)=0
F(7)=4
f(11)=7
una funzione suriettiva invece è un a funzione f:A->B tale che Im(f)=B ovvero deve essere una funzione che tocca tutti i valori di B
Ad esempio se A={1,2,3,4} e B={3,6,7,8] allora f tale che
f(1)=6
f(2)=3
f(3)=8
f(4)=7
è suriettiva perchè sono stati "toccati" tutti gli elementi di B.
Ovviamente una funzione iniettiva può non essere suriettiva e viceversa infatti la prima funzione che ti ho scritto era iniettiva ma non suriettiva perchè rimaneva fuori l'elemento 14 da B mentre quest'ultima è sia iniettiva che suriettiva(in questo caso si dice che è biiettiva)
P.S. Anche con questi esempi, sono riuscito a comprendere il concetto
Funzioni iniettive e suriettive?
Per esempio dato l'insieme A: {-1;5;7;11} e B: {0;4;7;9;14} definire una funzione iniettiva e una non iniettiva
Una funzione iniettiva f è tale che per ogni x e yche appartengono al tuo dominio si ha che f(x)=f(y) se e solo se x=y
In parole povere significa che la tua funzione deve associare ad ogni elemento un valore ma mai associare lo stesso valore a due elementi
Per esempio da A a B una funzione iniettiva può essere
f:A->B tale che
f(-1)=0
f(5)=9
f(7)=4
f(11)=7
Ovviamente puoi cambiare come vuoi le tue immagini basta che ti ricordi che per essere iniettiva non associ mai a due elementi lo stesso valore
una funzione non iniettiva è:
f(-1)=0
f(5)=0
F(7)=4
f(11)=7
una funzione suriettiva invece è un a funzione f:A->B tale che Im(f)=B ovvero deve essere una funzione che tocca tutti i valori di B
Ad esempio se A={1,2,3,4} e B={3,6,7,8] allora f tale che
f(1)=6
f(2)=3
f(3)=8
f(4)=7
è suriettiva perchè sono stati "toccati" tutti gli elementi di B.
Ovviamente una funzione iniettiva può non essere suriettiva e viceversa infatti la prima funzione che ti ho scritto era iniettiva ma non suriettiva perchè rimaneva fuori l'elemento 14 da B mentre quest'ultima è sia iniettiva che suriettiva(in questo caso si dice che è biiettiva)
P.S. Anche con questi esempi, sono riuscito a comprendere il concetto

"Bad90":
Scusami, ma si può fare la verifica del grafico della retta?
Sì. Ma, non potendo tu disegnare infinite rette, è sempre qualcosa di indicativo e di non propriamente rigoroso.
Perchè non mi è tanto chiaro graficamente questa biiettività
Puoi vederla come rapporto 1:1. Per ogni punto del dominio (sull'asse $x$) c'è un solo punto del codominio (sull'asse $y$) (funzione), e per ogni punto del codominio (suriettiva) c'è un solo punto del dominio (iniettiva).
Ma cosa devo fare in questi esercizi?

In cosa consiste la traccia? Cosa si fa per risolverlo?

In cosa consiste la traccia? Cosa si fa per risolverlo?
Le funzioni pari e dispari sono caratterizzate da simmetrie nei loro grafici, in particolare una funzione pari è simmetrica rispetto all'asse y e una funzione dispari è simmetrica rispetto all'origine degli assi $O(0;0)$. Questo dovrebbe esserti sufficiente per svolgere gli esercizi 











 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo