Feedback Shift Registers...

[Sk_Anonymous]

Ragazzi
oggi iniziamo un poco a parlare di un ‘accessorio’ molto utile in svariati campi della Matematica, dell’Informatica e delle Comunicazioni: il Feedback Shift Register. In figura è illustrato un diagramma schematico di FSR…



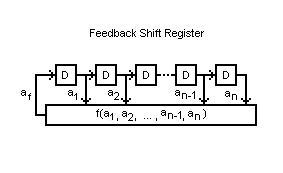
Il dispositivo consta di n elementi di memoria binari connessi in cascata chiamato shift register nel quale all’ingresso del primo elemento è inviata una variabile binaria che è funzione delle n variabili binarie contenute nello stesso. Le variabili binarie $a_i$, $i=1,2,…,n$, come dice il loro nome, possono assumere unicamente i valori $0$ e $1$. Con le variabili binarie è possibile eseguire le operazioni di somma e prodotto che altro non sono che le corrispondenti operazioni con gli interi il cui risultato è ridotto in complemento a $2$. In forma tabellare…

$0+0=0$, $0+1=1$, $1+0=1$, $1+1=0$

$0*0=0$, $0*1=0$, $1*0=0$, $1*1=1$ (1)

A ogni operazione di shift la variabile binaria contenuta in ognuno degli elementi di memoria del FSR è trasferita dall’ingresso all’uscita. Chiamando $in (k)$ la variabile ingresso e $out (k)$ la variabile di uscita ad un determinato ciclo $k$ sarà…

$out (k+1)=in (k)$ (2)

Osservando sempre la figura si deduce che per la variabile $a_f$ di uscita del FSR possiamo scrivere…

$a_1(k+1)= a_f (k)= f [a_1(k), a_2(k),…,a_(n-1)(k),a_n(k)]$ (3)

… dove $f (*)$ è una funzione tempo invariante delle $a_i$. Se la $f(*)$ è lineare il la (3) diviene …

$a_1(k+1)= sum_(i=1)^n c_i*a_i(k)$ (4)

… dove le costanti binarie $c_i$ sono chiamate ‘tappi’ [dall’inglese taps…] dello shift register il quale a sua volta è designato col nome di Linear Feedback Shift Register [LSFR]. Il polinomio di grado $n$ definito nel modo seguente…

$P(x)= 1+sum_(i=1)^n c_i*x^i$ (5)

… è usualmente chiamato [la ragione di ciò sarà evidente in seguito…] polinomio generatore. E’ evidente che la conoscenza dei coefficienti del polinomio generatore definisce completamente le caratteristiche del LFSR per cui nel seguito faremo riferimento costantemente ad esso. Un esempio di LFSR è illustrato nella seguente ‘animazione’…



In questo esempio è $n=16$ e il polinomio generatore è…

$P(x)= 1+x^11+x^13+x^14+x^16$ (6)

In un generico ciclo $k$ il vettore $A(k)= [a_1(k),a_2(k),…,a_(n-1)(k),a_n(k)]$ rappresenta lo stato del LFSR. In particolare il vettore $A(0)$ è detto stato iniziale del LFSR. E’ del tutto evidente dalla (4) che in caso sia $A(0)=[0,0,…,0,0]$ all'uscita del LFSR vi sarà la sequenza ‘tutti zeri’. Se invece lo stato inziale non è il vettore nullo la sequenza di uscita sarà periodica di periodo $m$, ossia…

$a_1(k)=a_1(k+m)$ (7)

Una breve riflessione consente di stabilire che $m<= 2^n-1$ e un LFSR per cui vale il segno ‘uguale’ è detto a massima periodicità. Il LFSR di ordine $16$ scelto come esempio è in effetti un LFSR a massima periodicità. Una domanda ovvia che dobbiamo porci è la seguente: quali caratteristiche deve avere $P(x)$ affinché il LFSR sia a massima periodicità?… Qualcuno di voi ne ha un’idea?…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[_luca.barletta]

$P(x)$ deve essere irriducibile mod2, ovvero non può essere fattorizzato con polinomi di grado $

Cita

Segnala

[Kroldar]

"lupo grigio":
Con le variabili binarie è possibile eseguire le operazioni di somma e prodotto che altro non sono che le corrispondenti operazioni con gli interi il cui risultato è ridotto in complemento a $2$. In forma tabellare…

$0+0=0$, $0+1=1$, $1+0=1$, $1+1=0$

$0*0=0$, $0*1=0$, $1*0=0$, $1*1=1$ (1)

Quelle che hai descritto sono due macchine combinatorie molto conosciute in ambito informatico. La prima è una porta logica xor (altresì detta or esclusivo), mentre la seconda è una porta logica and.

[Sk_Anonymous]

Esatto caro Kroldar!…

Per sapere se è vero o no quello che ha detto luca.barletta proviamo a fare qualche esempio. Prendiamo da prima $n=5$. In tal caso la periodicità massima della sequenza di stati del LFSR viene ad essere pari a $r=2^5-1=31$. Una [facile] ricerca sistematica sui polinomi di 5° grado in $GF(2^5)$ indica che i polinomi generatori con periodicità pari a 31 sono i seguenti [6 in totale]…

$P(x)=1+x^2+x^5$
$P(x)=1+x^3+x^5$
$P(x)=1+x+x^2+x^3+x^5$
$P(x)=1+x+x^2+x^4+x^5$
$P(x)=1+x+x^3+x^4+x^5$
$P(x)=1+x^2+x^3+x^4+x^5$ (1)

Il gentile lettore può [se vuole…] ‘divertirsi’ a provare a costruirsi il LFSR corrispondente ad uno di questi polinomi, inizializzarlo con un qualsiasi vettore di stato diverso dal vettore nullo, costruirsi la sequenza di stati generata da ogni shift e verificare che tale sequenza è periodica di periodo 31. Una interessante quanto ‘ovvia’ considerazione sui polinomi (1) è che essi sono irriducibili, ossia il polinomio di grado massimo che li divide è il polinomio di grado zero. Non è difficile poi dimostrare che i polinomi (1) sono gli unici polinomi di quinto grado irriducibili e pertanto per $n=5$ l’affermazione che condizione necessaria e sufficiente affinché $P(x)$ sia a massima periodicità è che sia irriducibile è vera. Vediamo ora che succede prendendo polinomi di grado maggiore, per esempio $n=6$. Ci si potrebbe ragionevolmente aspettare che rispetto al caso $n=5$ il numero dei polinomi generatori a massima periodicità sia all’incirca il doppio. Questo invece non avviene e si scopre che il numero di tali polinomi, i quali generano una sequenza di stati di periodicità $r=2^6-1=63$ è anche in questo caso uguale a 6…

$P(x)=1+x+x^6$
$P(x)=1+x+x^3+x^4+x^6$
$P(x)=1+x^5+x^6$
$P(x)=1+x+x^2+x^5+x^6$
$P(x)=1+x^2+x^3+x^5+x^6$
$P(x)=1+x+x^4+x^5+x^6$ (2)

Anche in questo caso tutti e i polinomi sono irriducibili, solo che, a differenza del caso $n=5$, essi non sono i soli polinomi irriducibili di grado 6. A titolo di esempio consideriamo…

$P(x)= 1+x^3+x^6$ (3)

Esso è di fatto irriducibile ma come polinomio generatore esso genera una sequenza di durata molto breve: 9. La verifica è presto eseguita applicando la formula ricorsiva…

$a_1(k+1)=a_3(k)+a_6(k)$ (4)

Inizializzando con $A(0)= [1,0,0,0,0,0]$ si ottiene la sequenza…

$A(1)=[0,1,0,0,0,0]$
$A(2)=[0,0,1,0,0,0]$
$A(3)=[1,0,0,1,0,0]$
$A(4)=[0,1,0,0,1,0]$
$A(5)=[0,0,1,0,0,1]$
$A(6)=[0,0,0,1,0,0]$
$A(7)=[0,0,0,0,1,0]$
$A(8)=[0,0,0,0,0,1]$
$A(9)=[1,0,0,0,0,0]=A(0)$ (5)

Va da sé che in questo caso l’uso di un polinomio irriducibile non è sufficiente a generare una sequenza di massima periodicità. Per comprendere esattamente le cose occorre indagare più a fondo sulle proprietà dei polinomi in $GF(2^n)$, cosa che faremo presto…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[TomSawyer1]

Infatti, luca.barletta ha detto che $2^n-1$ deve essere primo... Comunque, un polinomio su un campo di Galois, per generare un periodo di lunghezza massima deve essere anche primitivo.

[Sk_Anonymous]

L’affermazione secondo la quale si ‘deve’ scegliere $n$ in modo che $N=2^n-1$ sia primo [il che è lo stesso che dire che $n$ deve essere dispari dal momento che per $n$ pari $2^n-1$ è divisibile per $3$……] è un poco ‘azzardata’ e preclude da principio alcune possibili strade. La cosa in ogni caso deve essere meglio specificata e per far questo d’ora in poi farò riferimento allo schema di LFSR ‘modificato’ illustrato in figura…



La differenza rispetto allo schema ‘standard’ come si trova sulla maggior parte dei testi sono evidenti. Esso comunque è equivalente allo schema ‘standard’ nel senso che un generico polinomio di grado $n$…

$P(x)= 1+sum_(i=1)^n c_i*x^i$ (1)

… genera una sequenza della stessa lunghezza sia con lo schema ‘standard’ sia con lo schema ‘modificato’ . Il vantaggio dello schema ‘modificato’ stà nel fatto che se chiamiamo $S(x)$ il polinomio di grado $n-1$ corrispondente ad un certo stato $A(k)= [a_1, a_2,…,a_(n-1),a_n]$, vale a dire è…

$S_k(x)=sum_(i=1)^n a_i*x^(i-1)$ (2)

… una operazione di shift produce il nuovo stato…

$S_(k+1)(x)= x*S_k(x) mod P(x)$ (3)

Se lo stato iniziale $S_0(x)$ è il polinomio $x^0=1$ il LFSR genererà la sequenza di stati…

$S_k(x)=x^k mod P(x)$ (4)

…vale a dire le potenze di $x$ modulo $P(x)$. Prendiamo ad esempio $n=3$ e $P(x)= 1+x+x^3$. La sequenza di stati generata sarà…

$x^0=1$
$x^1=x$
$x^2=x^2$
$x^3=1+x$
$x^4=x+x^2$
$x^5=1+x+x^2$
$x^6=1+x^2$
$x^7=x^0=1…$ (5)

Essendo il polinomio scelto a massima periodicità la sequenza è di periodo $2^3-1=7$. E’ immediato osservare che i polinomi (5) con l’aggiunta del polinomio ‘nullo’ $x^(-oo)=0$, formano il $GF(2^3)$. La stessa cosa è vera naturalmente per altri valori di $n$ per i quali le condizioni di massima periodicità sono verificate. La scelta dello schema ‘modificato’ permette di sfruttare le proprietà dei campi di Galois e questo costituisce un sicuro ‘vantaggio’…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[_luca.barletta]

"lupo grigio":... si ‘deve’ scegliere $n$ in modo che $N=2^n-1$ sia primo [il che è lo stesso che dire che $n$ deve essere dispari dal momento che per $n$ pari $2^n-1$ è divisibile per $3$……]…

non è proprio la stessa cosa, controesempio:
n=9
$2^9-1=511=7*73$

Se invece intendi che N è sicuramente composto con n pari, ok.

[TomSawyer1]

lupo grigio, non sono due enunciati equivalenti quelli, anche se chiaramente $n$ deve essere dispari. Poi, non va bene la mia risposta? Cioè che devono essere anche primitivi, oltre ad irreducibili.

[_luca.barletta]

Non ho ancora capito perché le mie ipotesi erano "azzardate", la teoria dice quello.

[Sk_Anonymous]

Dunque, dunque... Visto che si vuole tirare in ballo la 'teoria' non sarà male andare a vedere in dettaglio che eredità ci ha lasciato al riguardo Evariste Galois...

Teoria dei campi finiti

Definizione: un campo finito è un campo di ordine finito, essendo l’ordine di un campo il numero di elementi del campo stesso. Un campo finito è chiamato anche campo di Galois

Proprietà fondamentale di un campo finito è che il suo ordine è sempre o un numero primo, oppure la potenza intera di un numero primo [Birkhoff e Mac Lane, 1996…]. Dato un numero primo $p$, questo genererà i campi finiti $GF

$,$GF[p^2]$,…,$GF[p^n]$,… rispettivamente di ordine $p$,$p^2$,…,$p^n$,… etc… Nel caso dei LFSR scegliamo $p=2$ di modo che un generico campo finito binario di grado $n$ sarà indicato come $GF[2^n]$. Se $n>1$, $GF[2^n]$ può essere rappresentato in forma isomorfa con la classe dei polinomi a coefficienti binari di grado inferiore ad $n$. Posto $2^n=N$ e indicati con $alpha_1$, $alpha_2$,…,$alpha_(N-1)$, gli elementi di $GF[2^n]$ diversi dall’elemento nullo, vale la relazione fondamentale…

$alpha_k= x^(k-1) mod P(x)$, $k=1,2,…,N-1$ (1)

… essendo $P(x)$ un polinomio di grado $n$ chiamato polinomio generatore del campo. Riguardo $P(x)$ di dimostra che condizione necessaria un polinomio di grado $n$ per essere polinomio generatore di $GF[2^n]$ è che sia irriducibile. Tuttavia [e lo si è dimostrato in precedenza…] tale condizione di norma non è sufficiente. Perciò un polinomio $P(x)$ che, facendo uso della (1), genera tutti gli elementi di $GF[2^n]$ è chiamato polinomio primitivo…

Questo [esposto in modo veramente ‘ridotto all’osso’…] è quanto afferma la ‘teoria’ al riguardo. In particolare non si fa alcun genere di ‘discriminazione’ riguardo ad $n$ tipo che esso sia ‘pari' piuttosto che ‘dispari’ o che $2^n-1$ sia o no ‘primo’…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[TomSawyer1]

"lupo grigio":… essendo $P(x)$ un polinomio di grado $n$ chiamato polinomio generatore del campo. Riguardo $P(x)$ di dimostra che condizione necessaria un polinomio di grado $n$ per essere polinomio generatore di $GF[2^n]$ è che sia irriducibile. Tuttavia [e lo si è dimostrato in precedenza…] tale condizione di norma non è sufficiente. Perciò un polinomio $P(x)$ che, facendo uso della (1), genera tutti gli elementi di $GF[2^n]$ è chiamato polinomio primitivo…

Io mi riferisco alla definizione piu' costruttiva (in questo caso) di polinomio primitivo. Cioe': se un polinomio e' irriducibile, allora e' anche primitivo, se l'emento particolare $x$ e' una radice primitiva del campo costruito usando il polinomio irriducibile.

[_luca.barletta]

La teoria, un po' più avanti, dice anche che in $GF(2^n)$, se $2^n-1$ è primo, il numero di polinomi primitivi eguaglia il numero di polinomi irriducibili.

[Sk_Anonymous]

Ragazzi
per affrontare la questione dei ‘polinomi irriducibili’ e dei ‘polinomi primitivi’ senza lasciarsi dietro delle ‘lacune’ è opportuno aprire una parentesi su due funzioni ‘discrete’ che nel proseguio si riveleranno assai utili. Entrambe sono legate a nomi di matematici illustri del passato e pertanto le indicherò di conseguenza…

La prima di queste è nota come ‘funzione $mu$ di Moebius’ ed è definita come…

$mu(n)= 0$, se $n$ ha uno o più fattori primi multipli, $1$ se $n=1$, $(-1)^k$ se $n$ è il prodotto di $k$ primi distinti (1)

Per $n=1,2,…$ sarà dunque $mu(n)=1, -1, -1, 0, -1, 1, -1, 0, 0, 1, -1, 0,...$. Anche se a prima vista essa può sembrare ‘arida’, la funzione $mu$ di Moebius gode di proprietà uniche che la rendono di primaria importanza in matematica discreta. Una delle più ‘suggestive’ tra queste è il legame alquanto particolare che lega la funzione $mu$ di Moebius alla funzione zeta di Riemann, legame dato dalla formula…

$1/(zeta(s))= sum_(n=1)^(oo) (mu(n))/(n^s)$ (2)

… dove è $Re>1$. Lo sviluppo (2) è ricavabile dall’espressione del cosiddetto ‘prodotto di Euler’ e chi è interessato alla procedura per ricavarla non ha difficoltà a trovarla in rete, ad esempio su http://mathworld.wolfram.com. Dalla (2) si ricavano conseguenze tra cui la ‘simpatica’ proprietà…

$sum_(n=1)^(oo) (mu(n))/n=0$ (3)

La seconda funzione ‘discreta’ che presentiamo è nota come ‘funzione $phi$ di Euler’, così definita…

$phi(n)=$ numero di interi positivi $primi relativi ad $n$ (4)

Due numeri $p$ e $q$ sono detti primi relativi se non hanno divisori comuni all’infuori di $1$. Per convenzione $1$ è considerato primo relativo con qualunque $n$. Se per esempio prendiamo $n=24$ gli interi primi relativi con esso saranno $1, 5, 7, 11, 13, 17, 19, 23$ per cui $phi(24)=8$. Sempre ‘per convenzione’ è $phi(0)=1$. Per $n>2$ $phi(n)$ è sempre pari. Inoltre se $p$ è primo sarà…

$phi(p)=p-1$ (5)

Si dimostra facilmente che se $m=p^alpha$ è la potenza intera di un numero primo è…

$phi(m)=phi(p^alpha)= p^alpha * (1-1/p)$ (6)

Con un ragionamento un poco più generale si dimostra che se un intero $m$ è scomponibile nel modo seguente…

$m=p_1^(alpha_1)*p_2^(alpha_2)*…*p_k^(alpha_k)$ (7)

… in cui le $p_i$, $I=1,2,…,k$ sono primi distinti, sarà…

$phi(m)= m*(1-1/(p_1))*(1-1/(p_2))*…*(1-1/(p_k))$ (8)

Nel caso già visto di $m=24$ I due ‘fattori primi’ sono $p_1=2$ e $p_2=3$ per cui…

$phi(24)= 24*(1-1/2)*(1-1/3)= 24*1/2*2/3= 8$ (9)

La funzione $phi$ di Eulero possiede tante altre proprietà che sarebbe qui lungo elencare e sulle quali torneremo al momento opportuno. Quello che interessa per ora mostrare è che la funzione $mu$ di Moebius e la funzione $phi$ di Euler sono legate fra loro. Per illustrare questa premettiamo la definizione di divisore di un intero. Se $d$ divide $m$ con allora $d$ è detto divisore di $m$. Per esempio $m=24$ ha per divisori $1,2,3,4,6,8,12,24$. Il legame che lega le due funzioni $mu$ e $phi$ è il seguente…

$phi(n)= sum_(d) d*mu(n/d)$ (10)

... dove la sommatoria è estesa a tutti i divisori di $n$. Se $n=24$ allora sarà…

$phi(24)= 1*mu(24)+2*mu(12)+3*mu(8)+4*mu(6)+6*mu(4)+8*mu(3)+12*mu(2)+24*mu(1)=$

$=1*0+2*0+3*0+4*1+6*0+8*(-1)+12*(-1)+24*1= 8$ (11)

Questo [per il momento…] è tutto quello che serve sapere sulle funzioni $mu$ e $phi$. Sperando di non avervi annoiato, mi riprometto di tornare più avanti su di esse…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[TomSawyer1]

Tutto cio' e' divertente,
ma piuttosto elementare..., Watson.

[Sk_Anonymous]

Che anche la formulazione matematica più complessa e impenetrabile sia fatta da mattoni ciascuno dei quali è di per sé stesso ‘elementare’ credo non ci piova… diversamente sarebbe materia per ‘alieni’… della cui ‘esistenza’ un simpatico forumista mi ha ‘sfidato’ a fornire la ‘prova matematica’…

A parte le 'facezie' proviamo a tornare ‘con i piedi per terra’ e affrontare il problema dei polinomi ‘irriducibili’ e dei polinomi ‘primitivi’. Che, fissato il grado $n$ e indicando con $L_i(n)$ e $L_p(n)$ il numero di polinomi irriducibili e primitivi di grado $n$ in $GF[2]$, sia $L_p(n)<=L_i(n)$ mi pare non ci siano dubbi. Il problema è stabilire quanto vale $L_i(n)$, quanto $L_q(n)$ ed eventualmente per quali $n$ è $L_i(n)=L_p(n)$. Rimandando ad un secondo tempo la ‘dimostrazione formale’ anticiperò i valori di entrambi. Il primo…


$L_i(n)= 1/n*sum_d mu(n/d)*2^d$ (1)

... essendo $mu(*)$ la funzione $mu$ di Moebious e $d$ un divisore di $n$. La serie deve essere estesa a tutti gli interi $d$ che dividono $n$. Il secondo…

$L_p(n)=1/n*phi(2^n-1)$ (2)

… essendo $phi(*)$ la funzione $phi$ di Euler. Ricordando la relazione che lega le due funzioni $mu$ e $phi$…

$phi(m)= sum_(d) d*mu(m/d)$ (3)

... dove $d$ è un generico divisore di $m$, la (2) può essere scritta anche come…

$L_p(n)= 1/n*sum_d d*mu((2^n-1)/d)$ (4)

... dove d è un generico divisore di $2^n-1$. E’ evidente dove sta la differenza tra la (1) e la (4). Ora poniamoci la domanda: per quali valori di $n$ la (1) e la (2) forniscono lo stesso risultato?… La risposta di primo acchito pare abbastanza semplice. Se $n$ è un numero primo, allora la (1) diviene…

$L_i(n)= 1/n*[mu(1)*2+mu(n)*2^n]=1/n*(-2+2^n)= 2/n*(2^(n-1)-1)$ (5)

Osservando la (2) invece si trova che se $2^n-1$ è un numero primo essa diviene...

$L_p(n)=2/n*(2^(n-1)-1)$ (6)

… ossia fornisce lo stesso valore della (6). Bene, bene… Quello che si può dire per ora è che condizione per la quale è $L_i(n)=L_p(n)$ è che $n$ e $2^n-1$ siano entrambi numeri primi. Perché sia vera l’affermazione secondo la quale condizione sufficiente è che $2^n-1$ sia un numero primo, è necessario dimostrare che se $2^n-1$ è un numero primo, allora anche $n$ è un numero primo. E’ proprio così?…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
alla domanda dell’ultimo post la risposta è ‘sì’ e proverò a far le cose ‘per bene’ dimostrando il seguente…

Teorema: dato un intero $n>1$, se $2^n-1$ è un numero primo, tale è anche $n$.

Cominciamo col rilevare che per ogni intero $n>1$ e per ogni $x$ reale vale l’identità…

$x^n -1= (x-1)*(x^(n-1)+x^(n-2)+...+x+1)$ (1)

Per $x=2$ la (1) diviene…

$2^n-1= 2^(n-1)+2^(n-2)+...+2+1$ (2)

Supponiamo ora per assurdo che $p=2^n-1$ sia un numero primo e $n$ non lo sia. In tal caso potremo porre $n=r*s$ ove $r$ ed $s$ sono interi entrambi $>1$. Ponendo ora nella (1) $x=2^r$ si ha…

$2^n-1= (2^r-1)*(2^(r*(s-1))+2^(r*(s-2))+…+2^r+1)$ (3)

Ora dalla (3) si deduce che $q=2^r-1ne1$ divide $2^n-1$ e questo contrasta con l’ipotesi di partenza. Pertanto $n$ deve necessariamente essere un numero primo.

Tale teorema ha un suggestivo…

Corollario: dati gli interi $a$ ed $n$ entrambi $>1$, se $p=a^n-1$ è un numero primo allora deve essere $n$ primo e $a=2$.

Abbiamo così verificato che, dato $n$, se $2^n-1$ è un numero primo allora l’insieme dei polinomi primi e dei polinomi irriducibili in $GF(2^n)$ coincidono e il loro numero è dato da…


$L_p(n)=2/n*(2^(n-1)-1)$ (4)

La ovvia domanda successiva è: per quali $n$ si verifica questa ‘circostanza fortunata’?… Risponderemo a ciò prossimamente…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
oggi ci dedichiamo un poco alla ‘storia’ e vediamo se, come dice un detto latino, essa è davvero magistra vitae. La questione riguardo al fatto che, dato un intero $n$ primo, $p=2^n-1$ fosse o no a sua volta primo risale addirittura alla ‘notte dei tempi’. Già il grande Euclide si occupò della cosa e trovò che $2^n-1$ era primo $n=2,3,5,7$. Da allora per secoli si è ritenuto che $p=2^n-1$ fosse primo per tutti gli $n$ primi fino a che nel 1536 Huldaricus Regius ha trovato che $p=2^11-1=2047=23*89$ non è un numero primo. All’inizio del ‘600 il matematico italiano Pietro Cataldi verifica che per n=17 e per n=19 $p=2^n-1$ è un numero primo e ipotizza che lo stesso vale per $n=23,29,31,37$. Quasi quaranta anni dopo Fermat dimostra che $p=2^23-1= 8388607 = 47*178481$ non è un numero primo e lo stesso vale per $p=2^37-1= 1374389553471 = 3*458129851157$. Deve passare un secolo intero perché si ottengano nuovi risultati su questo problema. Nel 1738 Euler dimostra che $p=2^29-1= 536870911=233*2304167$ non è un numero primo. Poco tempo dopo sempre Euler dimostra che $p=2^31-1=2147483647$, l’ultimo dei ‘numeri di Cataldi’, è un numero primo. La ‘lentezza’ dei progressi illustra chiaramente quanto era ‘difficile’ muoversi nel campo dei numeri primi nell’epoca in cui i calcoli dovevano essere fatti a mano.

Il matematico che più si è distinto in questo problema è però l’abate francese Marin Mersenne, vissuto tra la fine del ‘500 e la prima metà del ‘600, il quale nella prefazione della sua Cogitata Physic-Mathematica si spinge assai più in là dei contemporanei asserendo che $p=2^n-1$ è primo per $n=2,3,5,7,13,17,19,31,67,127,257$ e non è primo per tutti gli altri $n<257$. Anche se non del tutto esatta, per quei tempi si tratta di un risultato assai notevole e per questo i numeri del tipo $p=2^n-1$ sono oggi conosciuti col nome di ‘Numeri di Marsenne’. Un decisivo passo avanti nello studio del problema si è avuto solo tra la fine dell’800 e l’inizio del ‘900 per merito del matematico francese Anatole Lucas, al quale si deve il seguente…

Teorema: dato un numero primo $n$, il numero di Mersenne $p=2^n-1$ è primo se e solo se $p$ divide $S(n-1)$, dove $S(k+1)=S^2(k)-2$,$S(1)=4$

Il teorema consente l’implementazione di un test assai semplice per verificare se un numero di Mersenne è primo. Basta calcolare $S(n-1)$ modulo $2^n-1$ e verificare la condizione $S(n-1)_(mod p)=0$. Grazie a questo test Lucas e altri hanno potuto ‘controllare’ i risultati di Mersenne, trovando che l’abate del ‘600 aveva ‘indovinato’ per $n=127$, non aveva ‘indovinato’ per $n=67$ e $n=257$ ed inoltre aveva ‘tralasciato’ i casi $n=61$, $n=89$, $n=107$. A tutt’oggi la ‘lista’ del ‘Primi di Mersenne’ ha superato i $40$ elementi e ogni tanto qualcuno ne scopre uno 'nuovo'. Un caso abbastanza curioso è stata la ‘scoperta’ del 23-esimo primo di Mersenne, trovato alla University of Illinois. Il numero in questione è $p=2^11213-1$ ed il capo del dipartimento di matematica è stato talmente ‘orgoglioso’ del risultato conseguito dai suoi che ha dato disposizione di incollare sulla busta di ogni lettera ‘ufficiale’ la seguente etichetta…



Per concludere ‘in bellezza’ ecco qui di seguito la tabella dei ‘primi di Mersenne’ fino a $n=127$ [12 in tutto...], ciascuno con anno della scoperta e ‘scopritore’…

1 2
2 3
3 5
4 7
5 13 anonimo [1456]
6 17 Cataldi [1588]
7 19 Cataldi [1588]
8 31 Euler [1772]
9 61 Pervushin [1883]
10 89 Powers [1911]
11 107 Powers [1914]
12 127 Lucas [1876]


Bene ragazzi… per oggi è tutto…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
oggi riprendiamo il discorso aprendo una importante parentesi. Per il seguito sarà assai utile uno stretto legame [che può definirsi più a rigore isomorfismo…] esistente tra i polinomi di grado $n$ e le matrici $nxn$. Tale legame passa attraverso la definizione di polinomio caratteristico…

Supponiamo di avere un campo $K$ e una matrice $A$ di dimensioni $nxn$ su $K$. Il polinomio caratteristico di $A$, denotato come $P_A(x)$ è definito come…

$P_A(x)= det*(x*I-A)$ (1)

… dove $I$ è la matrice identità $n x n$. Dal momento che il determinante di una matrice è definito in termini di somme e prodotti l’espressione (1) è effettivamente un polinomio…

Due semplici esempi. Il primo con gli elementi del campo dei numeri reali…

$A=|(2,1),(-1,0)|$ (3)

$P_A(x)= det*(x*I-A)= det*|(x-2,-1),(1,x)| = x^2-2*x+1$ (4)

Il secondo con gli elementi di $GF[2]$…

$A=|(1,1),(0,1)|$ (5)

$P_A(x)= det*(x*I+A)= det *|(1+x,1),(0,1+x)|=1+x^2$ (6)

Per trovare il polinomio caratteristico di una matrice $A$ in base alla definizione data è pertanto necessario calcolarsi il determinante di una matrice $n x n$. Per il caso $n=2$ ciò è relativamente semplice. Nel caso $n=1023$ è un poco più complicato e vedremo prossimamente come si può fare. Per ora è tutto…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
riprendiamo oggi il discorso dal punto in cui eravamo rimasti, vale a dire il polinomio caratteristico di una matrice. Dal momento che siamo in $GF[2]$, d’ora in poi si terrà conto implicitamente di alcune proprietà dell’algebra modulo 2, in primo luogo del fatto che i segni $+$ e $–$ si equivalgono e pertanto quest’ultimo è sostituito ‘automaticamente’ dall’altro. Data un generica matrice $A$ di dimensioni $n x n$, si definisce polinomio caratteristico di $A$ il seguente…

$P_A (x)= det (x*I+A)$ (1)

Se indichiamo con $a_(i,j)$ il generico elemento di $A$ sarà…

$P_A(x)= det|(x+a_(1,1), a_(1,2),…, a_(1,n)),(a_(2,1),x+a_(2,2),…, a_(2,n)),(…,…,…,…), (a_(n,1),a_(n,2),…,x+a_(n,n))|$ (2)

Molto bene!… Ricordiamo ora alcune proprietà fondamentali dei determinanti, ‘adattandole’ all’algebra modulo 2. La prima afferma che se $B$ è ottenuta da $A$ scambiando la riga $j$ e la riga $k$ ovvero la colonna $j$ e la colonna $k$, allora è $det(B)=det(A)$ [a rigore sarebbe $det(B)=-det(A)$, ma nel nostro caso $+$ e $-$ coincidono…]. Da ciò possiamo dedurre la prima proprietà fondamentale…

Se $B$ è ottenuta da $A$ scambiando tra loro le righe $j$ e $k$ e le colonne $j$ e $k$, allora $A$ e $B$ hanno lo stesso polinomio caratteristico

Molto bene!… Una seconda proprietà dei determinanti stabilisce che se $B$ è ottenuta da $A$ sostituendo al posto della riga $j$ la somma delle righe $j$ e $k$, ovvero sostituendo al posto della colonna $j$ la somma delle colonne $j$ e $k$, allora è $det(B)=det(A)$. Da ciò possiamo dedurre la seconda proprietà fondamentale…

Se $B$ è ottenuta da $A$ sostituendo al posto della riga $j$ la somma delle righe $j$ e $k$ e al posto della colonna $k$ la somma delle colonne $j$ e $k$, allora $A$ e $B$ hanno lo stesso polinomio caratteristico

Queste due semplici regole ci saranno veramente utili e il perché lo vedremo tra poco…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
dopo esserci ‘rinfrescati la memoria’ su alcune [non difficili] proprietà dei determinanti, parliamo un poco di un particolare tipo di matrice, la cosiddetta Matrice di Hessenberg. Una matrice di dimensioni $nxn$ si definisce nella forma di Hessemberg se è così costruita…


$H=|(h_(1,1),h_(1,2), h_(1,3),…,h_(1,n-1),h_(1,n)), (h_(2,1),h_(2,2),h_(2,3),…,h_(2,n-1),h_(2,n)), (0,h_(3,2),h_(3,3),…,h_(3,n-1),h_(3,n)),(0,0,h_(4,3),…,h_(4,n-1),h_(4,n)),(…,…,…,…,…,…), (0,0,0,…,h_(n,n-1),h_(n,n))|$ (1)

… ossia è $h_(i,j)=0$ per $j
$P_A (x)= det (x*I+A)= det (x*I+H)$ (2)

… ovvero che abbia lo stesso polinomio caratteristico di $A$. A questo si arriva in maniera abbastanza agevole applicando le regole che abbiamo esaminato nello scorso postato attraverso. Tenendo presente che si indica con $R_k$ la riga $k$ e con $C_k$ la colonna $k$, il percorso è il seguente…

a) si pone $H=A$ e da ora in avanti si ‘lavora’ su $H$
b) per $j=1,2,…,n-2$ si cerca in $H$ il primo elemento non nullo in $h_(i,j)$ con $i=j+2,j+3,…,n$ e si indica con $m$ il valore corrispondente di $i$
c) se gli elementi $h_(i,j)$ con $j+1 d) si scambia $R_m$ con $R_(j+1)$ e $C_m$ con $C_(j+1)$
e) si cerca tra gli $h_(i,j)$ con $m<=i<=n$ il primo elemento non nullo e si indica ancora con $m$ il corrispondente valore di $i$
f) se gli elementi $h_(i,j)$ con $m<=i<=n$ sono tutti nulli si incrementa $j$ e si torna in b)
g) al posto di $R_m$ si pone $R_m+R_(j+1)$
h) al posto di $C_(j+1)$ si pone $C_m+C_(j+1)$
i) si torna in e)

Naturalmente la cosa risulterà più chiara con un esempio. Supponiamo di avere la matrice …

$A=|(0,1,1,1,1),(0,0,1,1,1),(1,1,1,0,0),(0,0,0,0,1),(1,1,1,1,1)|$ (3)

… per cui è…

$P_A(x)= det|(x,1,1,1,1),(0,x,1,1,1),(1,1,1+x,0,0),(0,0,0,x,1),(1,1,1,1,1+x)|$ (4)

Procedendo come indicato…

a) scambio di $R_2$ con $R_3$ e di $C_2$ con $C_3$…

$H=|(0,1,1,1,1),(1,1,1,0,0),(0,1,0,1,1),(0,0,0,0,1),(1,1,1,1,1)|$

b) $R_2+R_5$ al posto di $R_5$, $C_2+C_5$ al posto di $C_2$…

$H=|(0,0,1,1,1),(1,1,1,0,0),(0,0,0,1,1),(0,1,0,0,1),(0,1,0,1,1)|$

c) scambio di $R_3$ con $R_4$ e di $C_3$ con $C_4$…

$H=|(0,0,1,1,1),(1,1,0,1,0),(0,1,0,0,1),(0,0,1,0,1),(0,1,1,0,1)|$

d) $R_3+R_5$ al posto di $R_5$, $C_3+C_5$ al posto di $C_3$…

$H=|(0,0,0,1,1),(1,1,0,1,0),(0,1,1,0,1),(0,0,0,0,1),(0,0,1,0,0)|$

e) scambio di $R_4$ con $R_5$ e di $C_4$ con $C_5$…

$H=|(0,0,0,1,1),(1,1,0,0,1),(0,1,1,1,0),(0,0,1,0,0),(0,0,0,1,0)|$

La matrice finale $H$ è nella forma di Hessemberg ed ha lo stesso polinomio caratteristico della matrice da cui si è partiti. Pertanto sarà…

$P_A(x)= det |(x,0,0,1,1),(1,1+x,0,0,1),(0,1,1+x,1,0),(0,0,1,x,0),(0,0,0,1,x)|$ (5)

Come calcolare effettivamente il determinante (5), sfruttando il fatto che si tratta di una matrice di Hessenberg, lo vedremo prossimamente…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature

[Sk_Anonymous]

Ragazzi
eccoci di nuovo qui a parlare di Linear Feedback Shift Registers. Nella scorsa puntata abbiamo visto la tecnica per trasformare una qualsiasi matrice $A$ di dimensione $n x n$ nella forma di Hessemberg, vale a dire trovare la matrice $H$ di dimensione $n x n$ che abbia lo stesso polinomio caratteristico di $A$ e che goda della proprietà $h_(i,j)=0$ per $j
$P_A(x)= det (x*I+A)$ (1)

Il metodo ancora oggi più efficiente per il calcolo del determinante di una matrice è probabilmente l’algortimo noto con il nome di Sviluppo di Laplace. Esso fa uso del minore di una matrice $M$ che indichiamo con $c_(i,j)$ e definiamo come il determinante della sottomatrice ottenuta da $M$ elidendo la riga $i$ e la colonna $j$. Lo Sviluppo di Laplace per colonne calcola il determinante di $M$ con la formula…

$det(M)= sum_(i=1)^n (-1)^(i+j)*m_(i,j)*c_(i,j)$ (2)

In modo analogo di definisce lo Sviluppo di Laplace per righe. In sostanza lo Sviluppo di Laplace riduce il calcolo del determinante di ordine $n$ al calcolo di n determinanti di ordine $n-1$. Nel caso di una matrice di Hessemberg, dal momento che solo i due termini della prima colonna sono diversi da zero, ciascun passo richiede il solo calcolo di $2$ determinanti di grado $n-1$ e pertanto il carico computazionale risulta di molto alleggerito. Se $M$ è nella forma di Hessemberg il polinomio caratteristico si calcola applicando la formula iterativa seguente…

$P_k(x)= (x-m_(k,k))*P_(k-1) (x)-sum_(i=1)^(k-1) prod_(j-1)^(k-1) m_(j+1,j)*m_(i,k)*P_(k-i)(x), k=1,2,...,n$ (3)

... partendo da $P_0(x)=1$...

Il polinomio caratteristico di $M$ si ottiene calcolando iterativamente con la (3) $P_n(x)$. Riprendendo l’esempio della volta scorsa supponiamo di avere…


$A= |(0,1,1,1,1),(0,0,1,1,1),(1,1,1,0,0),(0,0,0,0,1),(1,1,1,1,1)|$ (4)

La matrice equivalente di $A$ nella forma di Hessenberg è stata calcolata e il polinomio caratteristico risultante è…

$P_A(x)= det |(x,0,0,1,1),(1,1+x,0,0,1),(0,1,1+x,1,0),(0,0,1,x,0),(0,0,0,1,x)|$ (5)

Applicando ora iterativamente la (3) si ottiene…

$P_A(x)= 1+x^2+x^5$ (6)

Bene ragazzi!… a questo punto abbiamo gli 'attrezzi' per proseguire il discorso sugli LFSR e ho la sensazione che verrà fuori qualcosa di ‘interessante’…

cordiali saluti

lupo grigio



An old wolf may lose his teeth, but never his nature