Feedback Shift Registers...
Ragazzi
oggi iniziamo un poco a parlare di un ‘accessorio’ molto utile in svariati campi della Matematica, dell’Informatica e delle Comunicazioni: il Feedback Shift Register. In figura è illustrato un diagramma schematico di FSR…
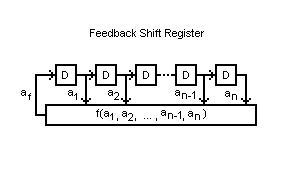
Il dispositivo consta di n elementi di memoria binari connessi in cascata chiamato shift register nel quale all’ingresso del primo elemento è inviata una variabile binaria che è funzione delle n variabili binarie contenute nello stesso. Le variabili binarie $a_i$, $i=1,2,…,n$, come dice il loro nome, possono assumere unicamente i valori $0$ e $1$. Con le variabili binarie è possibile eseguire le operazioni di somma e prodotto che altro non sono che le corrispondenti operazioni con gli interi il cui risultato è ridotto in complemento a $2$. In forma tabellare…
$0+0=0$, $0+1=1$, $1+0=1$, $1+1=0$
$0*0=0$, $0*1=0$, $1*0=0$, $1*1=1$ (1)
A ogni operazione di shift la variabile binaria contenuta in ognuno degli elementi di memoria del FSR è trasferita dall’ingresso all’uscita. Chiamando $in (k)$ la variabile ingresso e $out (k)$ la variabile di uscita ad un determinato ciclo $k$ sarà…
$out (k+1)=in (k)$ (2)
Osservando sempre la figura si deduce che per la variabile $a_f$ di uscita del FSR possiamo scrivere…
$a_1(k+1)= a_f (k)= f [a_1(k), a_2(k),…,a_(n-1)(k),a_n(k)]$ (3)
… dove $f (*)$ è una funzione tempo invariante delle $a_i$. Se la $f(*)$ è lineare il la (3) diviene …
$a_1(k+1)= sum_(i=1)^n c_i*a_i(k)$ (4)
… dove le costanti binarie $c_i$ sono chiamate ‘tappi’ [dall’inglese taps…] dello shift register il quale a sua volta è designato col nome di Linear Feedback Shift Register [LSFR]. Il polinomio di grado $n$ definito nel modo seguente…
$P(x)= 1+sum_(i=1)^n c_i*x^i$ (5)
… è usualmente chiamato [la ragione di ciò sarà evidente in seguito…] polinomio generatore. E’ evidente che la conoscenza dei coefficienti del polinomio generatore definisce completamente le caratteristiche del LFSR per cui nel seguito faremo riferimento costantemente ad esso. Un esempio di LFSR è illustrato nella seguente ‘animazione’…
In questo esempio è $n=16$ e il polinomio generatore è…
$P(x)= 1+x^11+x^13+x^14+x^16$ (6)
In un generico ciclo $k$ il vettore $A(k)= [a_1(k),a_2(k),…,a_(n-1)(k),a_n(k)]$ rappresenta lo stato del LFSR. In particolare il vettore $A(0)$ è detto stato iniziale del LFSR. E’ del tutto evidente dalla (4) che in caso sia $A(0)=[0,0,…,0,0]$ all'uscita del LFSR vi sarà la sequenza ‘tutti zeri’. Se invece lo stato inziale non è il vettore nullo la sequenza di uscita sarà periodica di periodo $m$, ossia…
$a_1(k)=a_1(k+m)$ (7)
Una breve riflessione consente di stabilire che $m<= 2^n-1$ e un LFSR per cui vale il segno ‘uguale’ è detto a massima periodicità. Il LFSR di ordine $16$ scelto come esempio è in effetti un LFSR a massima periodicità. Una domanda ovvia che dobbiamo porci è la seguente: quali caratteristiche deve avere $P(x)$ affinché il LFSR sia a massima periodicità?… Qualcuno di voi ne ha un’idea?…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
oggi iniziamo un poco a parlare di un ‘accessorio’ molto utile in svariati campi della Matematica, dell’Informatica e delle Comunicazioni: il Feedback Shift Register. In figura è illustrato un diagramma schematico di FSR…
Il dispositivo consta di n elementi di memoria binari connessi in cascata chiamato shift register nel quale all’ingresso del primo elemento è inviata una variabile binaria che è funzione delle n variabili binarie contenute nello stesso. Le variabili binarie $a_i$, $i=1,2,…,n$, come dice il loro nome, possono assumere unicamente i valori $0$ e $1$. Con le variabili binarie è possibile eseguire le operazioni di somma e prodotto che altro non sono che le corrispondenti operazioni con gli interi il cui risultato è ridotto in complemento a $2$. In forma tabellare…
$0+0=0$, $0+1=1$, $1+0=1$, $1+1=0$
$0*0=0$, $0*1=0$, $1*0=0$, $1*1=1$ (1)
A ogni operazione di shift la variabile binaria contenuta in ognuno degli elementi di memoria del FSR è trasferita dall’ingresso all’uscita. Chiamando $in (k)$ la variabile ingresso e $out (k)$ la variabile di uscita ad un determinato ciclo $k$ sarà…
$out (k+1)=in (k)$ (2)
Osservando sempre la figura si deduce che per la variabile $a_f$ di uscita del FSR possiamo scrivere…
$a_1(k+1)= a_f (k)= f [a_1(k), a_2(k),…,a_(n-1)(k),a_n(k)]$ (3)
… dove $f (*)$ è una funzione tempo invariante delle $a_i$. Se la $f(*)$ è lineare il la (3) diviene …
$a_1(k+1)= sum_(i=1)^n c_i*a_i(k)$ (4)
… dove le costanti binarie $c_i$ sono chiamate ‘tappi’ [dall’inglese taps…] dello shift register il quale a sua volta è designato col nome di Linear Feedback Shift Register [LSFR]. Il polinomio di grado $n$ definito nel modo seguente…
$P(x)= 1+sum_(i=1)^n c_i*x^i$ (5)
… è usualmente chiamato [la ragione di ciò sarà evidente in seguito…] polinomio generatore. E’ evidente che la conoscenza dei coefficienti del polinomio generatore definisce completamente le caratteristiche del LFSR per cui nel seguito faremo riferimento costantemente ad esso. Un esempio di LFSR è illustrato nella seguente ‘animazione’…
In questo esempio è $n=16$ e il polinomio generatore è…
$P(x)= 1+x^11+x^13+x^14+x^16$ (6)
In un generico ciclo $k$ il vettore $A(k)= [a_1(k),a_2(k),…,a_(n-1)(k),a_n(k)]$ rappresenta lo stato del LFSR. In particolare il vettore $A(0)$ è detto stato iniziale del LFSR. E’ del tutto evidente dalla (4) che in caso sia $A(0)=[0,0,…,0,0]$ all'uscita del LFSR vi sarà la sequenza ‘tutti zeri’. Se invece lo stato inziale non è il vettore nullo la sequenza di uscita sarà periodica di periodo $m$, ossia…
$a_1(k)=a_1(k+m)$ (7)
Una breve riflessione consente di stabilire che $m<= 2^n-1$ e un LFSR per cui vale il segno ‘uguale’ è detto a massima periodicità. Il LFSR di ordine $16$ scelto come esempio è in effetti un LFSR a massima periodicità. Una domanda ovvia che dobbiamo porci è la seguente: quali caratteristiche deve avere $P(x)$ affinché il LFSR sia a massima periodicità?… Qualcuno di voi ne ha un’idea?…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Risposte
Ragazzi
arrivati a questo punto cominciamo a parlare della applicazione tipica dei LFSR alla crittografia, i cosiddetti stream cipher. Supponiamo di avere un testo in chiaro [plaintext…] rappresentato mediante un alfabeto binario, ossia una sequenza di simboli $m_i$, $i=1,2,3,…$ con $m_i=0$ oppure $m_1=1$. Generiamo ora una chiave di cifratura [keystream…] rappresentata da un’altra sequenza binaria $k_i$, $i=1,2,3,…$. Si definisce testo cifrato [ciphertext…] la sequenza…
$c_i= m_i+k_i$, $i=1,2,3,…$ (1)
… ove l’operazione di somma è da intendersi ‘modulo $2$’. Il testo cifrato è ottenuto sommando al testo in chiaro la chiave di cifratura. La stessa operazione consente di ricavare dal testo cifrato il testo in chiaro. Se la chiave è una sequenza rigorosamente random’ ed è nota solamente al mittente e al legittimo destinatario del messaggio, la sicurezza della comunicazione è incondizionatamente garantita. E’ evidente che in pratica è impossibile realizzare sequenze rigorosamente random [ossia di periodo infinito…] e quello che si riesce a fare è realizzare frequenze di periodo ‘molto lungo’ che sono chiamate pseudorandom. Un metodo per generare una sequenza di questo tipo consiste nell’utilizzo della variabile in uscita da un LFSR, indicata in figura con $a_n$…
Si è visto che se $n$ è il gradi del polinomio caratteristico del LFSR e tale polinomio è primitivo, la periodicità della sequenza in uscita dal LFSR è pari a…
$N= 2^n-1$ (2)
Volendo utilizzare un LFSR come stream cipher è assai ‘intuitivo’ supporre che il ‘grado di sicurezza’ della comunicazione dipenderà fortemente…
a) dalla periodicità $N$ della chiave
b) dal numero $N_k$ di possibili chiavi
Nel caso di un LFSR assegnare una chiave equivale ad assegnare le seguenti due entità...
a) il polinomio caratteristico
b) lo ‘stato iniziale’
Si è visto in precedenza che se $2^n-1$ è primo [ossia un primo di Marsenne…] il numero di polinomi primi è pari a…
$L_p(n)= 2/n (2^(n-1)-1)$ (3)
Se dunque scegliamo $n$ in modo appropriato possiamo pensare di rappresentare la chiave con due numeri $n_1$ e $n_2$ con $1<=n_1<=L_p(n)$ e $1<=n_2<=2^n-1$. In tal caso il numero di possibili chiavi è dato da…
$N_k= (2^n-1)*L_p(n)$ (4)
Questo nell’ipotesi che si facciano le cose ‘al meglio’. Nella realtà, per una serie di ragioni alcune delle quali nulla hanno a che fare con la ‘Matematica’, le cose vanno in altro modo, come illustrato nell’esempio che segue…
Il sistema crittografico ‘Hughes XPD/KPD’ è creato nel 1986 dalla Hughes Aircraft Corporation. Equipaggia apparati militari radio destinati all’esportazione [XPD sta per Exportable Protection Device...]. L’algoritmo di cifratura è basato su un LFSR di 61-bit. Sono disponibili in tutto $2^10=1024$ polinomi primitivi, approvati dalla NSA [National Security Agency]. La chiave è data da uno di questi polinomi combinato allo stato iniziale del LFSR. Otto differenti funzioni non lineari ciascuno dei quali collegato a sei prese del LFSR producono una sequenza di byte usata per cifrare il messaggio. E’ ovvio che, essendo il sistema destinato alla ‘esportazione’, la NSA si è data da fare perché il ‘grado di sicurezza’ del sistema rientrasse [ampiamente…] nei limiti delle sue ‘capacità di decifrazione’
... In effetti con $n=61$ si ha…
$L_p(61)= (phi(2^61-1))/61=37,800,705,069,076,950$ (5)
… un numero dell’ordine di $2^55$, solo ‘leggermente superiore’ a $2^10=1024$ … A questo punto una domanda ‘ovvia’: perché non si è scelto un numero di polinomi primitivi superiore?… Uno dei motivi [non il solo…] è dato dal fatto che la ricerca preliminare di tutti i polinomi primitivi di grado $61$ e la loro ‘memorizzazione’ sono da considerare ‘operazioni praticamente infattibili’. Certo!… perché la cosa sia ‘fattibile’ sarebbe necessario ordinare prima tutti gli $L_p(61)$ polinomi primitivi in un archivio, di modo che, dato un numero $n_1$ con $1<=n_1<=L_p(61)$, si cerca il polinomio primitivo che occupa la ‘casella’ $n_1$ dell'archivio 
…
Sulle prime certo sembra un’impresa ‘un poco ardua’… però… sapete come son fatto ragazzi… mai dire mai!!!…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
arrivati a questo punto cominciamo a parlare della applicazione tipica dei LFSR alla crittografia, i cosiddetti stream cipher. Supponiamo di avere un testo in chiaro [plaintext…] rappresentato mediante un alfabeto binario, ossia una sequenza di simboli $m_i$, $i=1,2,3,…$ con $m_i=0$ oppure $m_1=1$. Generiamo ora una chiave di cifratura [keystream…] rappresentata da un’altra sequenza binaria $k_i$, $i=1,2,3,…$. Si definisce testo cifrato [ciphertext…] la sequenza…
$c_i= m_i+k_i$, $i=1,2,3,…$ (1)
… ove l’operazione di somma è da intendersi ‘modulo $2$’. Il testo cifrato è ottenuto sommando al testo in chiaro la chiave di cifratura. La stessa operazione consente di ricavare dal testo cifrato il testo in chiaro. Se la chiave è una sequenza rigorosamente random’ ed è nota solamente al mittente e al legittimo destinatario del messaggio, la sicurezza della comunicazione è incondizionatamente garantita. E’ evidente che in pratica è impossibile realizzare sequenze rigorosamente random [ossia di periodo infinito…] e quello che si riesce a fare è realizzare frequenze di periodo ‘molto lungo’ che sono chiamate pseudorandom. Un metodo per generare una sequenza di questo tipo consiste nell’utilizzo della variabile in uscita da un LFSR, indicata in figura con $a_n$…
Si è visto che se $n$ è il gradi del polinomio caratteristico del LFSR e tale polinomio è primitivo, la periodicità della sequenza in uscita dal LFSR è pari a…
$N= 2^n-1$ (2)
Volendo utilizzare un LFSR come stream cipher è assai ‘intuitivo’ supporre che il ‘grado di sicurezza’ della comunicazione dipenderà fortemente…
a) dalla periodicità $N$ della chiave
b) dal numero $N_k$ di possibili chiavi
Nel caso di un LFSR assegnare una chiave equivale ad assegnare le seguenti due entità...
a) il polinomio caratteristico
b) lo ‘stato iniziale’
Si è visto in precedenza che se $2^n-1$ è primo [ossia un primo di Marsenne…] il numero di polinomi primi è pari a…
$L_p(n)= 2/n (2^(n-1)-1)$ (3)
Se dunque scegliamo $n$ in modo appropriato possiamo pensare di rappresentare la chiave con due numeri $n_1$ e $n_2$ con $1<=n_1<=L_p(n)$ e $1<=n_2<=2^n-1$. In tal caso il numero di possibili chiavi è dato da…
$N_k= (2^n-1)*L_p(n)$ (4)
Questo nell’ipotesi che si facciano le cose ‘al meglio’. Nella realtà, per una serie di ragioni alcune delle quali nulla hanno a che fare con la ‘Matematica’, le cose vanno in altro modo, come illustrato nell’esempio che segue…
Il sistema crittografico ‘Hughes XPD/KPD’ è creato nel 1986 dalla Hughes Aircraft Corporation. Equipaggia apparati militari radio destinati all’esportazione [XPD sta per Exportable Protection Device...]. L’algoritmo di cifratura è basato su un LFSR di 61-bit. Sono disponibili in tutto $2^10=1024$ polinomi primitivi, approvati dalla NSA [National Security Agency]. La chiave è data da uno di questi polinomi combinato allo stato iniziale del LFSR. Otto differenti funzioni non lineari ciascuno dei quali collegato a sei prese del LFSR producono una sequenza di byte usata per cifrare il messaggio. E’ ovvio che, essendo il sistema destinato alla ‘esportazione’, la NSA si è data da fare perché il ‘grado di sicurezza’ del sistema rientrasse [ampiamente…] nei limiti delle sue ‘capacità di decifrazione’
... In effetti con $n=61$ si ha… $L_p(61)= (phi(2^61-1))/61=37,800,705,069,076,950$ (5)
… un numero dell’ordine di $2^55$, solo ‘leggermente superiore’ a $2^10=1024$
… A questo punto una domanda ‘ovvia’: perché non si è scelto un numero di polinomi primitivi superiore?… Uno dei motivi [non il solo…] è dato dal fatto che la ricerca preliminare di tutti i polinomi primitivi di grado $61$ e la loro ‘memorizzazione’ sono da considerare ‘operazioni praticamente infattibili’. Certo!… perché la cosa sia ‘fattibile’ sarebbe necessario ordinare prima tutti gli $L_p(61)$ polinomi primitivi in un archivio, di modo che, dato un numero $n_1$ con $1<=n_1<=L_p(61)$, si cerca il polinomio primitivo che occupa la ‘casella’ $n_1$ dell'archivio … Sulle prime certo sembra un’impresa ‘un poco ardua’… però… sapete come son fatto ragazzi… mai dire mai!!!…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Ragazzi
prima di entrare nel vivo dell’argomento un breve richiamo su alcune definizioni relative a GF[2^n]. Posto $p=2^n-1$, si definisce ‘radice primitiva’ del campo elemento $alpha$ tale che il minimo intero $k$ per cui è $alpha^k=1$ è pari a $p-1$. Designato quindi una radice primitiva $alpha$, gli elementi del campo sono dunque…
$[0,alpha^0,alpha,alpha^2,…,alpha^(p-1)]$ (1)
Supponiamo ora che gli elementi di $GF[2^n]$ siano matrici $n x n$ i cui elementi appartengono a $GF[2]$ e scegliamo come radice primitiva una qualunque matrice $A$ di dimensione $n x n$ tale che sia $A^p=I$, essendo $I$ la ‘matrice unitaria’. In tal caso un generico elemento non nullo di $GF[2^n]$ sarà $A^t$, con $t=1,2,…,p-1$. Indichiamo nel seguito con $P_t(x)$ il polinomio caratteristico di $A^t$. Ferme restando le definizioni di base ora fatte, diamo ora l’enunciato di alcuni teoremi la cui dimostrazione sarà data in un secondo momento [con la speranza di poter contare sul ‘fattivo aiuto’ da parte vostra ] …
a) per ogni valore di $t$ primo relativo con $p$, $P_t(x)$ è un polinomio primitivo
b) per ogni valore di $t$ primo relativo con $p$ gli elementi $A^t,A^(2t),…,A^(2^(n-1)*t)$ hanno lo stesso polinomio caratteristico
c) il numero di $t$ primi relativi con $p$ è dato da $phi(p)$, essendo $phi(*)$ la funzione di Eulero
d) ciascuno dei polinomi ottenuti in b) ha molteplicità pari a $n$, così che il numero di polinomi primitivi è pari a $(phi(p))/n$
Bene ragazzi!… cominciamo con un bell’esempio prendendo $n=5$, così che $p=2^5-1=31$. Siccome $p$ è un numero primo sarà $phi(p)=p-1$ e quindi il numero di polinomi primitivi in $GF[2^5]$ è $(p-1)/n=30/5=6$. Anni fa ho calcolato con paziente ricerca ‘esaustiva’ i polinomi primitivi da $GF[2^4]$ a $GF[2^14]$. Nel caso $n=5$ i sei polinomi sono i seguenti…
$1+x^2+x^3+x^4+x^5$
$1+x+x^2+x^4+x^5$
$1+x^3+x^5$
$1+x+x^3+x^4+x^5$
$1+x^2+x^5$
$1+x+x^2+x^3+x^5$ (2)
Il primo passo consiste nel trovare $alpha$, vale a dire una matrice $A$ di dimensione $5 x 5$ tale che $A^31=I$. Procedendo con una ricerca ‘random’ la prima matrice ‘buona’ trovata è stata…
$A=|(0,1,1,1,1),(1,0,0,0,1),(1,1,1,1,1),(0,1,0,1,0),(1,0,0,1,1)|$ (3)
Il polinomio caratteristico di $A^t$ per $t=1$ sarà…
$P_1(x)= 1+x+x^2+x^4+x^5$ (4)
In accordo col punto b) lo stesso sarà per $t=2, 4, 8, 16$. Per $t=3$ sarà…
$A^3= |(0,1,0,0,1),(0,0,0,0,1),(1,1,1,1,0),(0,0,1,1,1),(1,1,0,1,0)|$ (6)
… e il polinomio caratteristico…
$P_3(x)=1+x^3+x^5$ (7)
In accordo con punto b) lo stesso sarà per $t=6,12,24, 17$. Per $t=5$ sarà…
$A^5=|(0,1,0,1,0),(1,0,1,1,0),(0,1,0,0,0),(1,0,1,0,1),(1,0,0,0,0)|$ (8)
… e il polinomio caratteristico…
$P_5(x)=1+x+x^2+x^3+x^5$ (9)
In accordo col punto b) lo stesso sarà per $t=10,20,9, 18$. Per $t=7$ sarà…
$A^7=|(0,0,1,1,1),(1,0,1,0,0),(1,1,1,0,0),(1,1,0,0,1),(1,0,1,1,1)|$ (10)
… e il polinomio caratteristico…
$P_7=1+x^2+x^5$ (11)
In accordo con punto b) lo stesso sarà per $t=14,28,25, 19$. Per $t=11$ sarà…
$A^11=|(1,1,0,0,1),(0,1,0,0,1),(1,1,0,1,0),(0,0,1,0,0),(1,1,0,1,1)|$ (12)
… e il polinomio caratteristico…
$P_11(x)=1+x^2+x^3+x^4+x^5$ (13)
In accordo col punto b) lo stesso sarà per $t=22, 13, 25,21$. Per $t=15$ sarà…
$A^15=|(0,0,1,0,1),(0,0,1,1,1),(1,0,1,1,1),(1,1,1,1,1),(0,0,0,1,1)|$ (14)
… e il polinomio caratteristico…
$P_15(x)=1+x+x^3+x^4+x^5$ (15)
In accordo col punto b) lo stesso sarà per $t=30, 29, 27, 23$…
Molto bene ragazzi!… In tal modo, partendo da una sola matrice $5 x 5$, abbiamo costruito tutti i polinomi primitivi di $GF[2^5]$. Per ogni $t$ compreso tra $1$ e $30$, siamo ora in grado di calcolare il polinomio primitivo di quinto grado corrispondente $P_t(x)$. Siccome la stessa cosa può essere fatta per altri valori di $n$, apparirà subito chiara l’utilità della procedura che ora abbiamo appreso
… Già sarebbe un risultato notevole, ma occorrerà raffinarlo un pochino e approfondirne un poco anche l’aspetto formale per cui… non perdete le prossime puntate! …
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
prima di entrare nel vivo dell’argomento un breve richiamo su alcune definizioni relative a GF[2^n]. Posto $p=2^n-1$, si definisce ‘radice primitiva’ del campo elemento $alpha$ tale che il minimo intero $k$ per cui è $alpha^k=1$ è pari a $p-1$. Designato quindi una radice primitiva $alpha$, gli elementi del campo sono dunque…
$[0,alpha^0,alpha,alpha^2,…,alpha^(p-1)]$ (1)
Supponiamo ora che gli elementi di $GF[2^n]$ siano matrici $n x n$ i cui elementi appartengono a $GF[2]$ e scegliamo come radice primitiva una qualunque matrice $A$ di dimensione $n x n$ tale che sia $A^p=I$, essendo $I$ la ‘matrice unitaria’. In tal caso un generico elemento non nullo di $GF[2^n]$ sarà $A^t$, con $t=1,2,…,p-1$. Indichiamo nel seguito con $P_t(x)$ il polinomio caratteristico di $A^t$. Ferme restando le definizioni di base ora fatte, diamo ora l’enunciato di alcuni teoremi la cui dimostrazione sarà data in un secondo momento [con la speranza di poter contare sul ‘fattivo aiuto’ da parte vostra ] …
a) per ogni valore di $t$ primo relativo con $p$, $P_t(x)$ è un polinomio primitivo
b) per ogni valore di $t$ primo relativo con $p$ gli elementi $A^t,A^(2t),…,A^(2^(n-1)*t)$ hanno lo stesso polinomio caratteristico
c) il numero di $t$ primi relativi con $p$ è dato da $phi(p)$, essendo $phi(*)$ la funzione di Eulero
d) ciascuno dei polinomi ottenuti in b) ha molteplicità pari a $n$, così che il numero di polinomi primitivi è pari a $(phi(p))/n$
Bene ragazzi!… cominciamo con un bell’esempio prendendo $n=5$, così che $p=2^5-1=31$. Siccome $p$ è un numero primo sarà $phi(p)=p-1$ e quindi il numero di polinomi primitivi in $GF[2^5]$ è $(p-1)/n=30/5=6$. Anni fa ho calcolato con paziente ricerca ‘esaustiva’ i polinomi primitivi da $GF[2^4]$ a $GF[2^14]$. Nel caso $n=5$ i sei polinomi sono i seguenti…
$1+x^2+x^3+x^4+x^5$
$1+x+x^2+x^4+x^5$
$1+x^3+x^5$
$1+x+x^3+x^4+x^5$
$1+x^2+x^5$
$1+x+x^2+x^3+x^5$ (2)
Il primo passo consiste nel trovare $alpha$, vale a dire una matrice $A$ di dimensione $5 x 5$ tale che $A^31=I$. Procedendo con una ricerca ‘random’ la prima matrice ‘buona’ trovata è stata…
$A=|(0,1,1,1,1),(1,0,0,0,1),(1,1,1,1,1),(0,1,0,1,0),(1,0,0,1,1)|$ (3)
Il polinomio caratteristico di $A^t$ per $t=1$ sarà…
$P_1(x)= 1+x+x^2+x^4+x^5$ (4)
In accordo col punto b) lo stesso sarà per $t=2, 4, 8, 16$. Per $t=3$ sarà…
$A^3= |(0,1,0,0,1),(0,0,0,0,1),(1,1,1,1,0),(0,0,1,1,1),(1,1,0,1,0)|$ (6)
… e il polinomio caratteristico…
$P_3(x)=1+x^3+x^5$ (7)
In accordo con punto b) lo stesso sarà per $t=6,12,24, 17$. Per $t=5$ sarà…
$A^5=|(0,1,0,1,0),(1,0,1,1,0),(0,1,0,0,0),(1,0,1,0,1),(1,0,0,0,0)|$ (8)
… e il polinomio caratteristico…
$P_5(x)=1+x+x^2+x^3+x^5$ (9)
In accordo col punto b) lo stesso sarà per $t=10,20,9, 18$. Per $t=7$ sarà…
$A^7=|(0,0,1,1,1),(1,0,1,0,0),(1,1,1,0,0),(1,1,0,0,1),(1,0,1,1,1)|$ (10)
… e il polinomio caratteristico…
$P_7=1+x^2+x^5$ (11)
In accordo con punto b) lo stesso sarà per $t=14,28,25, 19$. Per $t=11$ sarà…
$A^11=|(1,1,0,0,1),(0,1,0,0,1),(1,1,0,1,0),(0,0,1,0,0),(1,1,0,1,1)|$ (12)
… e il polinomio caratteristico…
$P_11(x)=1+x^2+x^3+x^4+x^5$ (13)
In accordo col punto b) lo stesso sarà per $t=22, 13, 25,21$. Per $t=15$ sarà…
$A^15=|(0,0,1,0,1),(0,0,1,1,1),(1,0,1,1,1),(1,1,1,1,1),(0,0,0,1,1)|$ (14)
… e il polinomio caratteristico…
$P_15(x)=1+x+x^3+x^4+x^5$ (15)
In accordo col punto b) lo stesso sarà per $t=30, 29, 27, 23$…
Molto bene ragazzi!… In tal modo, partendo da una sola matrice $5 x 5$, abbiamo costruito tutti i polinomi primitivi di $GF[2^5]$. Per ogni $t$ compreso tra $1$ e $30$, siamo ora in grado di calcolare il polinomio primitivo di quinto grado corrispondente $P_t(x)$. Siccome la stessa cosa può essere fatta per altri valori di $n$, apparirà subito chiara l’utilità della procedura che ora abbiamo appreso
… Già sarebbe un risultato notevole, ma occorrerà raffinarlo un pochino e approfondirne un poco anche l’aspetto formale per cui… non perdete le prossime puntate! … cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Ragazzi
riprendiamo il discorso sui LFSR illustrando una loro caratteristica ‘negativa’, negativa al punto da precludere in pratica il loro utilizzo in crittografia. Abbiamo esaminato in...
https://www.matematicamente.it/f/viewtopic.php?t=20802
... la particolare tecnica di attacco grazie alla quale Eva è riuscita a mettere in chiaro un messaggio di Alice destinato a Bob: la tecnica know plaintext attack. Tale tecnica consiste nel tentativo di ricostruire la chiave di un testo cifrato rintracciando la posizione di porzioni del testo in chiaro di cui si conosce il contenuto. Ora dimostreremo che uno stream cipher realizzato con LFSR è particolarmente vulnerabile a tale tipo di attacco. Se il LFSR è formato da $n$ elementi di memoria vedremo ora che basta sia nota una sequenza del testo in chiaro di lunghezza $2*n-1$ per ricostruire la chiave e decifrare l’intero messaggio…
Si è visto in precedenza che nel caso di un LSFR la ‘chiave’ è costituita da due elementi e precisamente…
a) il polinomio generatore
b) lo stato iniziale
Il numero possibile di chiavi di un LFSR di ordine $n$ è dunque dato dal prodotto…
$N_k= (2^n-1)*L_p(n)$ (1)
… essendo $L_p(n)$ il numero di polinomi primitivi di grado $n$. Si è visto anche che se $n$ è un primo di Marsenne si ha…
$L_p(n)= 2/n *(2^(n-1)-1)$ (2)
Ora indichiamo una sequenza binaria finita di $k$ termini $s_0,s_1,…,s_(k-1)$ con la notazione $s^k$. Si dice che un LSFR genera $s^k$ se, partendo sa uno stato iniziale noto, genera una sequenza i cui primi $k$ termini sono $s^k$. Ok… definiamo ora che cosa si intende per complessità lineare di una sequenza binaria finita $s^k$:
Si definisce come complessità lineare di una sequenza binaria finita $s^k$ e si indica con la notazione $L(s^k)$ la lunghezza del più corto LFSR che genera $s^k$
Della complessità lineare di una sequenza binaria finita si potrebbe parlare a lungo e chi è interessato può trovare ampio materiale al riguardo in rete. Qui citiamo solamente quello che ci interessa, cominciando con il seguente teorema fondamentale …
Teorema: se un polinomio $P(x)$ di grado $n$ è irriducibile, allora ognuno dei $2^n-1$ stati iniziali non nulli di un LFSR di grado $n$ e di polinomio caratteristico $P(x)$ produce una sequenza di uscita $s$ di complessità lineare $L(s)=n$
Andiamo ora avanti definendo in un successivo step un’altra importante funzione: il profilo di complessità lineare di una sequenza binaria finita…
Sia $s^k$ una sequenza binaria di lunghezza $k$ e sia $L(s^k)$ la sua complessità lineare. Si definisce profilo di complessità lineare di $s^k$ la sequenza $L_1,L_2,…,L_k$ delle complessità lineari delle sottosequenze di $s^k$ $s^i$, $i=1,2,…,k$
Facciamo un esempio per chiarire meglio le cose. Consideriamo la seguente sequenza finita di lunghezza $k=20$…
$s^20= 1 0 0 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 1 0$ (3)
Il corrispondente profilo di complessità lineare è dato da…
$L_i= 1 1 1 3 3 3 3 5 5 5 6 6 6 8 8 8 9 9 10 10$ (4)
… ed è rappresentato nel diagramma seguente…
Come si può vedere il profilo di complessità lineare ‘non si distacca di molto’ dalla retta di pendenza $L=i/2$. Questa caratteristica contraddistingue le sequenze cosiddette pseudorandom. Prossimamente vedremo come utilizzare le nozioni apprese oggi…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
riprendiamo il discorso sui LFSR illustrando una loro caratteristica ‘negativa’, negativa al punto da precludere in pratica il loro utilizzo in crittografia. Abbiamo esaminato in...
https://www.matematicamente.it/f/viewtopic.php?t=20802
... la particolare tecnica di attacco grazie alla quale Eva è riuscita a mettere in chiaro un messaggio di Alice destinato a Bob: la tecnica know plaintext attack. Tale tecnica consiste nel tentativo di ricostruire la chiave di un testo cifrato rintracciando la posizione di porzioni del testo in chiaro di cui si conosce il contenuto. Ora dimostreremo che uno stream cipher realizzato con LFSR è particolarmente vulnerabile a tale tipo di attacco. Se il LFSR è formato da $n$ elementi di memoria vedremo ora che basta sia nota una sequenza del testo in chiaro di lunghezza $2*n-1$ per ricostruire la chiave e decifrare l’intero messaggio…
Si è visto in precedenza che nel caso di un LSFR la ‘chiave’ è costituita da due elementi e precisamente…
a) il polinomio generatore
b) lo stato iniziale
Il numero possibile di chiavi di un LFSR di ordine $n$ è dunque dato dal prodotto…
$N_k= (2^n-1)*L_p(n)$ (1)
… essendo $L_p(n)$ il numero di polinomi primitivi di grado $n$. Si è visto anche che se $n$ è un primo di Marsenne si ha…
$L_p(n)= 2/n *(2^(n-1)-1)$ (2)
Ora indichiamo una sequenza binaria finita di $k$ termini $s_0,s_1,…,s_(k-1)$ con la notazione $s^k$. Si dice che un LSFR genera $s^k$ se, partendo sa uno stato iniziale noto, genera una sequenza i cui primi $k$ termini sono $s^k$. Ok… definiamo ora che cosa si intende per complessità lineare di una sequenza binaria finita $s^k$:
Si definisce come complessità lineare di una sequenza binaria finita $s^k$ e si indica con la notazione $L(s^k)$ la lunghezza del più corto LFSR che genera $s^k$
Della complessità lineare di una sequenza binaria finita si potrebbe parlare a lungo e chi è interessato può trovare ampio materiale al riguardo in rete. Qui citiamo solamente quello che ci interessa, cominciando con il seguente teorema fondamentale …
Teorema: se un polinomio $P(x)$ di grado $n$ è irriducibile, allora ognuno dei $2^n-1$ stati iniziali non nulli di un LFSR di grado $n$ e di polinomio caratteristico $P(x)$ produce una sequenza di uscita $s$ di complessità lineare $L(s)=n$
Andiamo ora avanti definendo in un successivo step un’altra importante funzione: il profilo di complessità lineare di una sequenza binaria finita…
Sia $s^k$ una sequenza binaria di lunghezza $k$ e sia $L(s^k)$ la sua complessità lineare. Si definisce profilo di complessità lineare di $s^k$ la sequenza $L_1,L_2,…,L_k$ delle complessità lineari delle sottosequenze di $s^k$ $s^i$, $i=1,2,…,k$
Facciamo un esempio per chiarire meglio le cose. Consideriamo la seguente sequenza finita di lunghezza $k=20$…
$s^20= 1 0 0 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 1 0$ (3)
Il corrispondente profilo di complessità lineare è dato da…
$L_i= 1 1 1 3 3 3 3 5 5 5 6 6 6 8 8 8 9 9 10 10$ (4)
… ed è rappresentato nel diagramma seguente…
Come si può vedere il profilo di complessità lineare ‘non si distacca di molto’ dalla retta di pendenza $L=i/2$. Questa caratteristica contraddistingue le sequenze cosiddette pseudorandom. Prossimamente vedremo come utilizzare le nozioni apprese oggi…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Ragazzi
oggi descriviamo un efficiente algoritmo, ideato da Berlekamp e Massey, per il calcolo della complessità lineare di una sequenza binaria di $k$ termini. L’algoritmo poggia in primo luogo sulla seguente definizione…
Consideriamo la sequenza binaria finita $s^(k+1)=s_0,s_1,…,s_(k-1),s_k$. Data la sua sottosequenza $s^k=s_0,s_1,…,s_(k-1)$ di complessità lineare $L$, sia $[L,P(x)]$ con $P(x)=1+c_1*x+c_2*x^2+…+c_L*x^L$ il LFSR che genera la sequenza $s^k$. Si definisce ‘prossima discrepanza’ e si indica con $d_k$ la differenza modulo $2$ tra $s_k$ e il termine di indice $k$ generato dal LFSR, ossia…
$d_k=s_k+ sum_(i=1)^L c_i*s_(k-i)$ (1)
… e in secondo luogo sul seguente teorema…
Teorema: sia $s^k=s_0,s_1,…,s_(k-1)$ una sequenza binaria finita di complessità lineare $L$ e sia $[L,P(x)]$ il LFSR che genera $s^k$. In tal caso…
a) lo stesso LFSR genera $s^(k+1)=s_0,s_1,…,s_(k-1),s_k$ se e solo se la prossima discrepanza $d_k$ è uguale a $0$
b) se $d_k=0$ allora $L(s^(k+1))=L$
c) se $d_k=1$ sia $m$ il massimo intero minore di $k$ per cui $L(s^m)
$L’= L$ se $L>k/2$
$L’=k+1-L$ se $L<=k/2$ (2)
$P’(x)= P(x)+Q(x)*x^(k-m)$ (3)
Sulla base della definizione e del teorema associato che abbiamo ora enunciato è stato sviluppato l’algoritmo di Berlekamp-Massey che qui riportiamo…
Dati in ingresso: una sequenza binaria $s^k=s_0,s_1,…,s_(k-1)$ di lunghezza $k$
Dato in uscita: la complessità lineare $L(s^k)$
1) Inizializzazione
Si pone $P(x)=1$, $L=0$, $m=-1$, $Q(x)=1$, $p=0$
2) Per ogni $p$ con $0<=p
2.1 calcola $d= s_p+sum_(i=1)^L c_i*s_(p-i)$
2.2 se $d=1$ fa così…
$T(x)=P(x)$, $P(x)=T(x)+Q(x)*x^(p-m)$, se $L<=k/2$ fa così…
$M=L$, $L=p+1-M$, $m=p$, $Q(x)=T(x)$
2.3 incrementa $p$
Al termine di ogni iterazione si ha un LFSR $[L,P(x)]$ di minima lunghezza che genera la sottosequenza $s^p$. L’algoritmo dunque genera il profilo di complessità lineare definito in precedenza. Se $k$ è la lunghezza della sequenza il numero di oprazioni necessarie è proporzionale a $k^2$. La potenza di questo algoritmo è veramente notevole in quanto permette di concludere i seguenti due corollari al teorema già citato…
Corollario a: sia $s^k$ una sequenza binaria di lunghezza $k$ e complessità lineare $L$. Il LFSR di lunghezza $L$ che genera $s^k$ è unico se e solo se è $L<=k/2$.
Corollario b: sia $s$ una sequenza binaria infinita di complessità lineare $L$ e sia $t$ una sottosequenza di $s$ di lunghezza almeno $2L$. In tal caso l’algoritmo di Berlekamp-Massey fornisce lunghezza $L$ e polinomio generatore $P(x)$ del LFSR di lunghezza minima che genera $s$
L’ultimo corollario pone in pratica una severa limitazione all’uso di un LFSR come stream cipher. Se $n$ è la lunghezza del LFSR e il polinomio generatore $P(x)$ è primitivo sappiamo che la periodicità della senza generata vale $2^n-1$. Purtroppo il teorema ora visto consente di ricavare la lunghezza $n$ e il polinomio generatore $P(x)$ del LFSR usato, ovvero in parole povere la chiave di cifratura, se è nota una sottosequenza della chiave di lunghezza $2*n$. Questo rende tali dispositivi estremamente vulnerabili ad attacchi del tipo know plaintext, aventi lo scopo di arrivare alla chiave attraverso la conoscenza di alcuni frammenti del testo in chiaro. Per avere un’idea della efficacia di tale tipo di attacco consideriamo il caso di un LFSR di grado $n=61$. In precedenza si è visto che il numero delle chiavi [polinomi primitivi] in questo caso risulta pari a…
$L_p(61)= 37.800.705.069.076.950$ (4)
… vale a dire un numero pari a circa 38 milioni di miliardi e la lunghezza della sequenza generata è alcune decine di volte maggiore. Ebbene con l’impiego dell’algoritmo ora visto dalla conoscenza di una sottosequenza della chiave di sole $k=122$ cifre binarie è possibile individuare tra tutte quelle chiavi quella ‘giusta’ …
Per finire un bell’esempio con un numero un poco più basso di $61$… diciamo $n=5$… Supponiamo di avere la sequenza $s^k$ di lunghezza $9$ seguente…
$s^k= 0 0 1 1 0 1 1 1 0$ (5)
Qui di seguito è eseguito step by step l’algoritmo di Berlekamp-Massey…
$p=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=1$,$s_1=0$,$d=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=2$,$s_2=0$,$d=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=3$,$s_3=1$,$d=1$,$T(x)=1$,$P(x)=1+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=4$,$s_4=1$,$d=1$,$T(x)=1+x^3$,$P(x)=1+x+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=5$,$s_5=0$,$d=1$,$T(x)=1+x+x^3$,$P(x)=1+x+x^2+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=6$,$s_6=1$,$d=1$,$T(x)=1+x+x^2+x^3$,$P(x)=1+x+x^2$,$L=3$,$m=2$,$Q(x)=1$
$p=7$,$s_7=1$,$d=0$,$T(x)=1+x+x^2+x^3$,$P(x)=1+x+x^2$,$L=3$,$m=2$,$Q(x)=1$
$p=8$,$s_8=1$,$d=1$,$T(x)=1+x+x^2$,$P(x)=1+x+x^2+x^5$,$L=5$,$m=7$,$Q(x)=1+x+x^2$
$p=9$,$s_9=0$,$d=1$,$T(x)=1+x+x^2+x^5$,$P(x)=1+x^3+x^5$,$L=5$,$m=7$,$Q(x)=1+x+x^2$
Il LFSR a lunghezza minima che genera la (5) ha pertanto lunghezza $L=5$ e polinomio generatore $P(x)=1+x^3+x^5$… semplice no?
…
cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
oggi descriviamo un efficiente algoritmo, ideato da Berlekamp e Massey, per il calcolo della complessità lineare di una sequenza binaria di $k$ termini. L’algoritmo poggia in primo luogo sulla seguente definizione…
Consideriamo la sequenza binaria finita $s^(k+1)=s_0,s_1,…,s_(k-1),s_k$. Data la sua sottosequenza $s^k=s_0,s_1,…,s_(k-1)$ di complessità lineare $L$, sia $[L,P(x)]$ con $P(x)=1+c_1*x+c_2*x^2+…+c_L*x^L$ il LFSR che genera la sequenza $s^k$. Si definisce ‘prossima discrepanza’ e si indica con $d_k$ la differenza modulo $2$ tra $s_k$ e il termine di indice $k$ generato dal LFSR, ossia…
$d_k=s_k+ sum_(i=1)^L c_i*s_(k-i)$ (1)
… e in secondo luogo sul seguente teorema…
Teorema: sia $s^k=s_0,s_1,…,s_(k-1)$ una sequenza binaria finita di complessità lineare $L$ e sia $[L,P(x)]$ il LFSR che genera $s^k$. In tal caso…
a) lo stesso LFSR genera $s^(k+1)=s_0,s_1,…,s_(k-1),s_k$ se e solo se la prossima discrepanza $d_k$ è uguale a $0$
b) se $d_k=0$ allora $L(s^(k+1))=L$
c) se $d_k=1$ sia $m$ il massimo intero minore di $k$ per cui $L(s^m)
$L’= L$ se $L>k/2$
$L’=k+1-L$ se $L<=k/2$ (2)
$P’(x)= P(x)+Q(x)*x^(k-m)$ (3)
Sulla base della definizione e del teorema associato che abbiamo ora enunciato è stato sviluppato l’algoritmo di Berlekamp-Massey che qui riportiamo…
Dati in ingresso: una sequenza binaria $s^k=s_0,s_1,…,s_(k-1)$ di lunghezza $k$
Dato in uscita: la complessità lineare $L(s^k)$
1) Inizializzazione
Si pone $P(x)=1$, $L=0$, $m=-1$, $Q(x)=1$, $p=0$
2) Per ogni $p$ con $0<=p
2.1 calcola $d= s_p+sum_(i=1)^L c_i*s_(p-i)$
2.2 se $d=1$ fa così…
$T(x)=P(x)$, $P(x)=T(x)+Q(x)*x^(p-m)$, se $L<=k/2$ fa così…
$M=L$, $L=p+1-M$, $m=p$, $Q(x)=T(x)$
2.3 incrementa $p$
Al termine di ogni iterazione si ha un LFSR $[L,P(x)]$ di minima lunghezza che genera la sottosequenza $s^p$. L’algoritmo dunque genera il profilo di complessità lineare definito in precedenza. Se $k$ è la lunghezza della sequenza il numero di oprazioni necessarie è proporzionale a $k^2$. La potenza di questo algoritmo è veramente notevole in quanto permette di concludere i seguenti due corollari al teorema già citato…
Corollario a: sia $s^k$ una sequenza binaria di lunghezza $k$ e complessità lineare $L$. Il LFSR di lunghezza $L$ che genera $s^k$ è unico se e solo se è $L<=k/2$.
Corollario b: sia $s$ una sequenza binaria infinita di complessità lineare $L$ e sia $t$ una sottosequenza di $s$ di lunghezza almeno $2L$. In tal caso l’algoritmo di Berlekamp-Massey fornisce lunghezza $L$ e polinomio generatore $P(x)$ del LFSR di lunghezza minima che genera $s$
L’ultimo corollario pone in pratica una severa limitazione all’uso di un LFSR come stream cipher. Se $n$ è la lunghezza del LFSR e il polinomio generatore $P(x)$ è primitivo sappiamo che la periodicità della senza generata vale $2^n-1$. Purtroppo il teorema ora visto consente di ricavare la lunghezza $n$ e il polinomio generatore $P(x)$ del LFSR usato, ovvero in parole povere la chiave di cifratura, se è nota una sottosequenza della chiave di lunghezza $2*n$. Questo rende tali dispositivi estremamente vulnerabili ad attacchi del tipo know plaintext, aventi lo scopo di arrivare alla chiave attraverso la conoscenza di alcuni frammenti del testo in chiaro. Per avere un’idea della efficacia di tale tipo di attacco consideriamo il caso di un LFSR di grado $n=61$. In precedenza si è visto che il numero delle chiavi [polinomi primitivi] in questo caso risulta pari a…
$L_p(61)= 37.800.705.069.076.950$ (4)
… vale a dire un numero pari a circa 38 milioni di miliardi e la lunghezza della sequenza generata è alcune decine di volte maggiore. Ebbene con l’impiego dell’algoritmo ora visto dalla conoscenza di una sottosequenza della chiave di sole $k=122$ cifre binarie è possibile individuare tra tutte quelle chiavi quella ‘giusta’
… Per finire un bell’esempio con un numero un poco più basso di $61$… diciamo $n=5$… Supponiamo di avere la sequenza $s^k$ di lunghezza $9$ seguente…
$s^k= 0 0 1 1 0 1 1 1 0$ (5)
Qui di seguito è eseguito step by step l’algoritmo di Berlekamp-Massey…
$p=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=1$,$s_1=0$,$d=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=2$,$s_2=0$,$d=0$,$T(x)=0$,$P(x)=1$,$L=0$,$m=-1$,$Q(x)=1$
$p=3$,$s_3=1$,$d=1$,$T(x)=1$,$P(x)=1+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=4$,$s_4=1$,$d=1$,$T(x)=1+x^3$,$P(x)=1+x+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=5$,$s_5=0$,$d=1$,$T(x)=1+x+x^3$,$P(x)=1+x+x^2+x^3$,$L=3$,$m=2$,$Q(x)=1$
$p=6$,$s_6=1$,$d=1$,$T(x)=1+x+x^2+x^3$,$P(x)=1+x+x^2$,$L=3$,$m=2$,$Q(x)=1$
$p=7$,$s_7=1$,$d=0$,$T(x)=1+x+x^2+x^3$,$P(x)=1+x+x^2$,$L=3$,$m=2$,$Q(x)=1$
$p=8$,$s_8=1$,$d=1$,$T(x)=1+x+x^2$,$P(x)=1+x+x^2+x^5$,$L=5$,$m=7$,$Q(x)=1+x+x^2$
$p=9$,$s_9=0$,$d=1$,$T(x)=1+x+x^2+x^5$,$P(x)=1+x^3+x^5$,$L=5$,$m=7$,$Q(x)=1+x+x^2$
Il LFSR a lunghezza minima che genera la (5) ha pertanto lunghezza $L=5$ e polinomio generatore $P(x)=1+x^3+x^5$… semplice no?
… cordiali saluti
lupo grigio
An old wolf may lose his teeth, but never his nature
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo