Il teorema piu' bello
Qual e' secondo voi il piu' bel teorema della matematica?
Risposte
Il teorema più bello? Quello di Noether.
Sokal?
Anche lui ha qualche limite.
Vi invito a leggere questo:
http://www.swif.uniba.it/lei/rassegna//990616.htm
Fa bene alla salute leggere cosa dicono "gli altri"
per una rassegna, vedasi:
http://lgxserver.uniba.it/lei/rassegna/sokal.htm
Anche lui ha qualche limite.
Vi invito a leggere questo:
http://www.swif.uniba.it/lei/rassegna//990616.htm
Fa bene alla salute leggere cosa dicono "gli altri"
per una rassegna, vedasi:
http://lgxserver.uniba.it/lei/rassegna/sokal.htm
"Lorenzo Pantieri":
Bello scherzo sì, ma il fisico Alan Sokal ne ha combinato uno anche peggiore.
Sì, avevo già sentito parlare di questo bel tiro...

La filosofia è una componente fondamentale del sapere umano e si può dire che tutti coloro che si mettono a riflettere su qualche questione in fondo fanno della filosofia, anche se non ne sono coscienti.
Forse si può dire che la filosofia è come l'aria, tutti la respiriamo senza farci troppo caso tuttavia se qualcuno si mette ad inquinarla per fare i propri interessi è un guaio per tutta la comunità...
Sokal di certo ha voluto attirare l'attenzione sul fatto che in ambito filosofico dove non c'è una solida pietra di paragone come può essere la logica per la matematica, gli esperimenti per la fisica o il semplice funzionamento di una macchina per l'ingegneria, l'inquinamento è molto, molto facile...
Il teorema piu bello che conosco è il teorema delle dimensioni.
"Cozza Taddeo":
[quote="Lorenzo Pantieri"][quote="Cozza Taddeo"]Senza dubbio il lemma di Zakovskyj.
Uh?
Che lemma è? Su Internet non ho trovato niente...

Ero curioso di vedere quanto sarebbe durato il mio bluff...solo una decina di ore (quasi)...pensavo di farla franca per almeno qualche giorno...'sti matematici se non vanno al fondo delle cose non sono soddisfatti!!!
In ogni caso sono contento che sia stato tu a smascherarmi.
Per quel poco che so di matematica penso che l'Ultimo Teorema di Fermat sia un buon candidato ad essere nominato teorema più bello.
Ma anche il teorema dei quattro colori non è per niente male...[/quote]
Bello scherzo sì, ma il fisico Alan Sokal ne ha combinato uno anche peggiore.
Per chi non conoscesse i fatti, o li avesse dimenticati, nella primavera del 1996 il fisico Alan Sokal mandò alla rivista Social Text un lungo articolo intitolato "Trasgredire le frontiere: verso un'ermeneutica trasformativa della gravità quantistica", che fu prontamente pubblicato benché fosse infarcito di assurdità messevi a bella posta, mascherate in "filosofese". La conclusione che Sokal e altri trassero dalla vicenda fu che, poiché certa filosofia non si distingue dalla sua parodia, non è una cosa seria.
Allargando il discorso, si tratta di vicende che hanno risvolti epistemologici mica da ridere. Per esempio:
1. Si dice sempre che il bello di una dimostrazione matematica è che tutti, in linea di principio, possono ripeterla per conto proprio. Tuttavia ci sono dimostrazioni, come quella dell'Ultima Teorema di Fermat, che per essere affontate richiedono anni e anni di studi specialistici. In pratica, solo pochissime persone al mondo possono seguire una dimostrazione come quella per (cercare di) controllarne l'esattezza. La probabilità che sia sfuggito un'errore, a mio giudizio, esiste.
2. Si dice sempre che uno dei cardini della fisica sperimentale sia la riproducibilità degli esperimenti. Tuttavia, ci sono esperimenti che durano anni, richiedono il lavoro di centinaia di scienziati e costano decine e decine di milioni. In pratica, è impossibile per chiunque ripetere esperimenti di questo genere.
Insomma, l'epistemologia della scienza qui è ancora tutta da scrivere.
Ciao,
L.
P.S. Onorato di essere stato io a smascherarti!
madonna sta rigorosità mi perseguita.. 

ma io uso queste cifre, nell'ordine:
0,1,2,3,5,4,6,7,8,9





0,1,2,3,5,4,6,7,8,9
ok
mi riferisco ad una numerazione in base 10 e l'operatore $+$ è quello che noi comunemente chiamiamo addizione..
mi riferisco ad una numerazione in base 10 e l'operatore $+$ è quello che noi comunemente chiamiamo addizione..
"Mega-X":
secondo me il teorema più bello è quello che dice che $2+2=4$..
Occhio: tieni presente che se non specifichi per bene le ipotesi, a differenza di quello che pensa la maggior parte della gente, $2+2$ non fa sempre $4$...
Senz'ombra di dubbio:
il teorema fondamentale del calcolo integrale.
il teorema fondamentale del calcolo integrale.
secondo me il teorema più bello è quello che dice che $2+2=4$.. 

Secondo me, Teorema fondamentale dell'Aritmetica (spiega le fondamenta di un argomento che tutti conoscono fin dalle scuole medie inferiori).
E' poi interessante studiare come tale teorema si generalizzi per un qualsiasi dominio fattoriale.
E' poi interessante studiare come tale teorema si generalizzi per un qualsiasi dominio fattoriale.
Aggiungo alla lista anche l'infinità dei numeri primi e la scomposizione in fattori primi.
"Sandokan.":
Qual e' secondo voi il piu' bel teorema della matematica?
Per quel poco che so, il Teorema Fondamentale dell'Algebra.
Senza dubbio il Nullstellensatz, nella seguente forma:
"Se k è un campo algebricamente chiuso allora gli ideali massimali di $k[X_1,...,X_n]$ sono del tipo $(X_1-a_1,...,X_n-a_n)$ con $a_1,...,a_n \in k$."
Non è difficilissimo da dimostrare, ma senza dubbio è geniale.
"Se k è un campo algebricamente chiuso allora gli ideali massimali di $k[X_1,...,X_n]$ sono del tipo $(X_1-a_1,...,X_n-a_n)$ con $a_1,...,a_n \in k$."
Non è difficilissimo da dimostrare, ma senza dubbio è geniale.
Bello scherzetto Cozza Taddeo 

"Lorenzo Pantieri":
[quote="Cozza Taddeo"]Senza dubbio il lemma di Zakovskyj.
Uh?
Che lemma è? Su Internet non ho trovato niente...

Ero curioso di vedere quanto sarebbe durato il mio bluff...solo una decina di ore (quasi)...pensavo di farla franca per almeno qualche giorno...'sti matematici se non vanno al fondo delle cose non sono soddisfatti!!!
In ogni caso sono contento che sia stato tu a smascherarmi.
Per quel poco che so di matematica penso che l'Ultimo Teorema di Fermat sia un buon candidato ad essere nominato teorema più bello.
Ma anche il teorema dei quattro colori non è per niente male...
"Cozza Taddeo":
Senza dubbio il lemma di Zakovskyj.
Uh?
Che lemma è? Su Internet non ho trovato niente...
"John_Nash":
Bellissima sta cosa! Non l'avevo mai sentita!!
Io l'ho letta per la prima volta proprio su Lettera Matematica Pristem, nella versione cartacea presente nella biblioteca universitaria.
Credo che l'appellativo di miracolo sia centratissimo e vederlo funzionare in modo dinamico con Cabri o un qualunque altro sw di geometria dinamica è quasi impressionante.
Quando poi ho scoperto l'estensione della seconda figura sono rimasto senza parole, così come quando ho trovato proprio quella figura su Mathworld.com. Ma l'ho ugualmente inserito nella mia tesi. Ed esiste anche una generalizzazione ulteriore, che però non sono mai riuscito a mettere bene a fuoco: con costruzioni analoghe si possono creare 27 triangoli di cui 18 equilateri.
"desko":
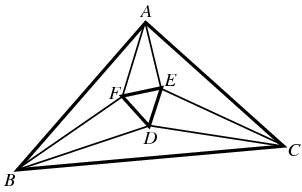
Ai tanti già citati ne aggiungo uno poco conosciuto: il miracolo di Morley
La cosa quasi sorprendente è che pur essendo un teorema di geometria euclidea piana piuttosto semplice (almenoo nell'enunciato) è stato scoperto solo nel 1899.
In sostanza trisecando gli angoli interni di un triangolo qualsiasi si ottiene un triangolo equilatero
Bellissima sta cosa! Non l'avevo mai sentita!!
E un'altra molto bella nella pagina che hai citato tu è questa:

Teorema di Napoleone. In un triangolo, si costruiscano i triangoli equilateri sui lati, esternamente ai lati stessi. I centri di questi triangoli equilateri costituiscono i vertici di un triangolo equilatero.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo