Il teorema piu' bello
Qual e' secondo voi il piu' bel teorema della matematica?
Risposte
Senza dubbio il lemma di Zakovskyj.
decisamente il teorema di Koepke
Ai tanti già citati ne aggiungo uno poco conosciuto: il miracolo di Morley
La cosa quasi sorprendente è che pur essendo un teorema di geometria euclidea piana piuttosto semplice (almenoo nell'enunciato) è stato scoperto solo nel 1899.
In sostanza trisecando gli angoli interni di un triangolo qualsiasi si ottiene un triangolo equilatero
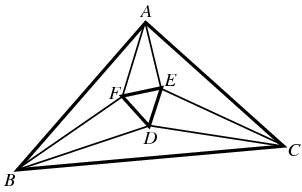
Appena lo lessi iniziai a giocarci un po' con Cabri e mi chiesi cosa succede se si trisecano gli angoli esterni.
Arrivai a questo, illudendomi di essere stato il primo:
La cosa quasi sorprendente è che pur essendo un teorema di geometria euclidea piana piuttosto semplice (almenoo nell'enunciato) è stato scoperto solo nel 1899.
In sostanza trisecando gli angoli interni di un triangolo qualsiasi si ottiene un triangolo equilatero
Appena lo lessi iniziai a giocarci un po' con Cabri e mi chiesi cosa succede se si trisecano gli angoli esterni.
Arrivai a questo, illudendomi di essere stato il primo:
"Lorenzo Pantieri":
[quote="Sandokan."]Qual e' secondo voi il piu' bel teorema della matematica?
Bella domanda. Teoremi facili da dimostrare, ma tremendamente eleganti (e densi di conseguenze):
1. L'irrazionalità di $\sqrt{2}$.
2. Il teorema di Cantor: $\RR$ non è equipotente ad $\NN$.
3. "L'insieme $A$ non è equipotente all'insieme delle parti di $A$."[/quote]
Aggiungerei a questi le formule di Cardano e quelle di Ferrari per le equazioni di terzo e quarto grado, tenendo conto con quali mezzi le hanno trovate.
In generale, comunque per me il piu' bello e' il Theorema Aureum, di Gauss.
La formula di Eulero naturalmente!
E anche il lemmino di Zorn sempre sempre usato...
E anche il lemmino di Zorn sempre sempre usato...
"Sandokan.":
Qual e' secondo voi il piu' bel teorema della matematica?
Bella domanda. Teoremi facili da dimostrare, ma tremendamente eleganti (e densi di conseguenze):
1. L'irrazionalità di $\sqrt{2}$.
2. Il teorema di Cantor: $\RR$ non è equipotente ad $\NN$.
3. "L'insieme $A$ non è equipotente all'insieme delle parti di $A$."
Poi direi anche:
4. I teoremi di Goedel.
5. Il teorema di Galois: $S_n$ non è risolubile con $n>5$.
Ciao,
L.
no, non lo sapevo. grazie dell'informazione.
"wedge":
nella mia opinione... teorema di Gauss-Bonnet
Come saprai, il teorema da te citato e' un caso estremamente particolare del teorema dell'indice di Atiyah–Singer. Quello si' che e' un risultato prodigioso! Chissa' se un giorno saro' in grado di leggerne la dimostrazione...
nella mia opinione... teorema di Gauss-Bonnet
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo