Brogli alle ultime elezioni politiche?... ma no!!!...
Ragazzi
è passato oltre un anno dalle elezioni politiche, sulle quali ancora aleggia [da parte della attuale ‘opposizione’ ma non solo…] l’ombra di possibili ‘brogli’. Su questo argomento un celebre ‘giornalista’ [non certo etichettabile come appartenente alla ‘destra’…] ha costruito nientemeno che un film dal titolo Uccidete la democrazia!. Tale ‘film’ [il cui ‘successo’ conseguito in termini di audience mi è del tutto sconosciuto…] verte intorno alla seguente ‘trama’: il ministero degli interni avrebbe nella circostanza, tramite un rocambolesco software importato dagli Usa, ‘trasformato’ un gran numero di schede ‘bianche’ in voti validi. Come ben si sa l’assoluta inconsistenza di tale ‘trama’ è apparsa subito evidente, al punto che il ‘giornalista’ in questione è stato rinviato a giudizio con l’accusa di calunnia. A parte però le ‘tesi’ più o meno demenziali di costui, che cosa si può dire della presunta ‘metamorfosi’ delle schede?… è verosimile l’ipotesi che un numero ‘insolitamente elevato’ [rispetto alle precedenti tornate elettorali nelle quali tale numero sarebbe stato ‘fisiologico’… ] di schede bianche siano divenute ‘per magia’ schede valide?… Dal momento che siamo in un sito di ‘matematici’ vediamo di fornire una risposta di tipo ‘matematico’ al quesito…
Tanto per avviare il discorso riporto qui la ‘distribuzione’ delle sezioni con un determinato numero di schede bianche avutesi nel Comune di Roma [2600 sezioni in totale]…
schede bianche/numero sezioni
0 / 199
1 / 396
2 / 487
3 / 521
4 / 380
5 / 250
6 / 161
7 / 92
8 / 54
9 / 31
10 / 14
11 / 10
12 / 0
13 / 3
14 / 1
15 / 0
16 / 0
17 / 1
numero totale sezioni: 2600
Qui potete vedere gli stessi dati tradotti in un diagramma…

Tanto per cominciare una domanda per gli ‘esperti’ di ‘statistica’ [ ]: è tutto ‘ok’ nel diagramma qui sopra o vi sembra ci sia qualche ‘stranezza’?…
]: è tutto ‘ok’ nel diagramma qui sopra o vi sembra ci sia qualche ‘stranezza’?…
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature
è passato oltre un anno dalle elezioni politiche, sulle quali ancora aleggia [da parte della attuale ‘opposizione’ ma non solo…] l’ombra di possibili ‘brogli’. Su questo argomento un celebre ‘giornalista’ [non certo etichettabile come appartenente alla ‘destra’…] ha costruito nientemeno che un film dal titolo Uccidete la democrazia!. Tale ‘film’ [il cui ‘successo’ conseguito in termini di audience mi è del tutto sconosciuto…] verte intorno alla seguente ‘trama’: il ministero degli interni avrebbe nella circostanza, tramite un rocambolesco software importato dagli Usa, ‘trasformato’ un gran numero di schede ‘bianche’ in voti validi. Come ben si sa l’assoluta inconsistenza di tale ‘trama’ è apparsa subito evidente, al punto che il ‘giornalista’ in questione è stato rinviato a giudizio con l’accusa di calunnia. A parte però le ‘tesi’ più o meno demenziali di costui, che cosa si può dire della presunta ‘metamorfosi’ delle schede?… è verosimile l’ipotesi che un numero ‘insolitamente elevato’ [rispetto alle precedenti tornate elettorali nelle quali tale numero sarebbe stato ‘fisiologico’… ] di schede bianche siano divenute ‘per magia’ schede valide?… Dal momento che siamo in un sito di ‘matematici’ vediamo di fornire una risposta di tipo ‘matematico’ al quesito…
Tanto per avviare il discorso riporto qui la ‘distribuzione’ delle sezioni con un determinato numero di schede bianche avutesi nel Comune di Roma [2600 sezioni in totale]…
schede bianche/numero sezioni
0 / 199
1 / 396
2 / 487
3 / 521
4 / 380
5 / 250
6 / 161
7 / 92
8 / 54
9 / 31
10 / 14
11 / 10
12 / 0
13 / 3
14 / 1
15 / 0
16 / 0
17 / 1
numero totale sezioni: 2600
Qui potete vedere gli stessi dati tradotti in un diagramma…

Tanto per cominciare una domanda per gli ‘esperti’ di ‘statistica’ [
cordiali saluti
lupo grigio

an old wolf may lose his teeth, but never his nature
Risposte
Riesumo questo vecchio post perchè ci sono di nuovo state le elezioni politiche.
Ebbene anche stavolta si sono ripetute le 3 presunte anomalie del 2006.
Nel 2006 si trovava anomalo che ci fossero state solo 440mila schede bianche.
Perchè si diceva che dovessero essere almeno un milione e mezzo.
E il milione mancante l'inchiesta di Deaglio sosteneva che fosse stato trasformato in voti per Forza Italia con dei brogli.
Ebbene,però le schede bianche sono invece rimaste basse pure le volte successive,senza il CDX al ministero a poter imbrogliare.
Furono:
485000 nel 2008
395000 nel 2013
Adesso nel 2018 sono 350000 anche se manca il dato del Lazio.
Quindi sono in linea col 2006.
A meno di non sostenere che il CDX abbia fatto brogli pure nel 2008,2013 e 2018 c'è da ritenere che col nuovo sistema elettorale
gli italiani votino meno schede bianche.
La seconda anomalia sono i sondaggi errati.
Nel 2006 per i sondaggi il CSX doveva vincere di molto ed invece ci fu il pareggio.
Adesso i sondaggi hanno stimato correttamente il CDX al 37%.
Hanno però sbagliato M5S e CSX.
I sondaggi davano tipo M5S al 28% e CSX al 27%.
Invece è finita M5S al 32,7% e CSX al 22,8%.
Infine il trend di scrutinio.
Nel 2006 il CSX con 7122 sezioni scrutinate su 61000 era al 52%,poi però con la progressione dello spoglio calò al 49,8%
finale.
E pareva statisticamente impossibile,come scrisse Odifreddi.
Oggi con 11000 sezioni scrutinate il PD aveva circa il 20,8% circa.
Poi è calato fino al 18,7% finale.
Però sempre perchè per primi arrivano più dati dalle regioni rosse dove il PD è più forte che nel resto del paese.
Ecco un grafico con l'andamento del PD durante lo spoglio:
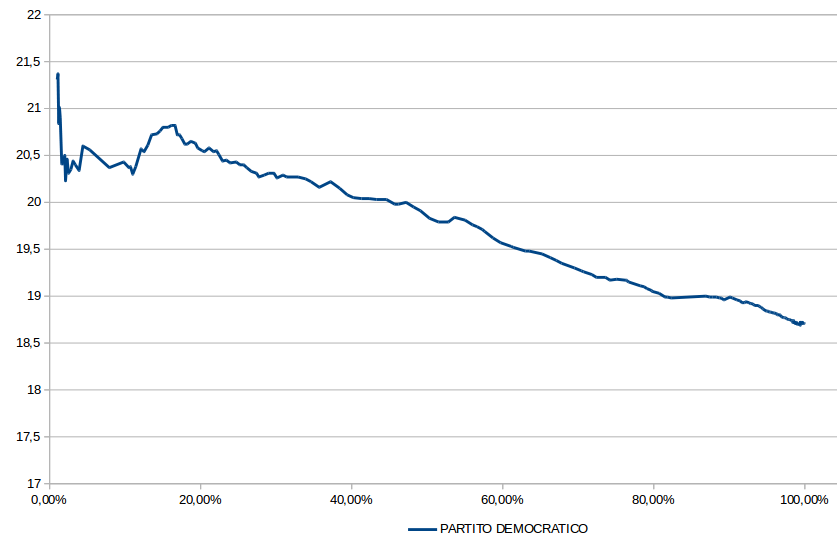
Non sarà proprio come nel 2006,che nel 2006 vi erano solo 2 coalizioni,però la tendenza è simile.
Il PD quasi sempre cala.
Chiedo scusa se ho riesumato questo vecchio post.
Però vedo che c'è ancora un pò di gente che si crede la bufala dei brogli nel 2006.
Ebbene anche stavolta si sono ripetute le 3 presunte anomalie del 2006.
Nel 2006 si trovava anomalo che ci fossero state solo 440mila schede bianche.
Perchè si diceva che dovessero essere almeno un milione e mezzo.
E il milione mancante l'inchiesta di Deaglio sosteneva che fosse stato trasformato in voti per Forza Italia con dei brogli.
Ebbene,però le schede bianche sono invece rimaste basse pure le volte successive,senza il CDX al ministero a poter imbrogliare.
Furono:
485000 nel 2008
395000 nel 2013
Adesso nel 2018 sono 350000 anche se manca il dato del Lazio.
Quindi sono in linea col 2006.
A meno di non sostenere che il CDX abbia fatto brogli pure nel 2008,2013 e 2018 c'è da ritenere che col nuovo sistema elettorale
gli italiani votino meno schede bianche.
La seconda anomalia sono i sondaggi errati.
Nel 2006 per i sondaggi il CSX doveva vincere di molto ed invece ci fu il pareggio.
Adesso i sondaggi hanno stimato correttamente il CDX al 37%.
Hanno però sbagliato M5S e CSX.
I sondaggi davano tipo M5S al 28% e CSX al 27%.
Invece è finita M5S al 32,7% e CSX al 22,8%.
Infine il trend di scrutinio.
Nel 2006 il CSX con 7122 sezioni scrutinate su 61000 era al 52%,poi però con la progressione dello spoglio calò al 49,8%
finale.
E pareva statisticamente impossibile,come scrisse Odifreddi.
Oggi con 11000 sezioni scrutinate il PD aveva circa il 20,8% circa.
Poi è calato fino al 18,7% finale.
Però sempre perchè per primi arrivano più dati dalle regioni rosse dove il PD è più forte che nel resto del paese.
Ecco un grafico con l'andamento del PD durante lo spoglio:

Non sarà proprio come nel 2006,che nel 2006 vi erano solo 2 coalizioni,però la tendenza è simile.
Il PD quasi sempre cala.
Chiedo scusa se ho riesumato questo vecchio post.
Però vedo che c'è ancora un pò di gente che si crede la bufala dei brogli nel 2006.
Riesumo questo vecchio post,oltre per fare i complimenti a Lupo Grigio per la sua analisi attenta,per dire la mia sull'argomento.(non sono un matematico,ma un editor di un blog di sondaggi e politica)
La tesi del software che avrebbe dirottato le bianche su Forza Italia non regge.
Per il semplice fatto che i dati del sito del ministero non hanno valore legale ai fini della proclamazione del risultato vero e proprio.
Essa avviene tramite il riconteggio di tutti i verbali cartacei originali di tutte e 60000 le sezioni italiane,
che dopo essere stati scrutinati nel seggio confluiscono a Roma alla Corte di Cassazione che ricontandoli appunto
fa le somme dei partiti e delle coalizioni e proclama i risultati ufficiali e definitivi.
In questi verbali naturalmente ci sono anche le schede bianche segnate.
Ora,quando nel 2006 i giudici hanno fatto i conti il risultato che è uscito è stato davvero di 19 milioni a testa per le coalizioni e di solo 440000 schede bianche.
Se fosse come inizialmente diceva Deaglio,e cioè del dato del sito del ministero alterato,allora rifacendo i conti
sui verbali originali sarebbe dovuta uscire una grande differenza tra le coalizioni,cioè 19 per il CSX,ma meno di 18 per il CDX.
Perchè le bianche anzichè solo 440000 dovevano risultare più di un milione e mezzo.(la teoria appunto era che il CDX in un qualche modo le avesse trasformate in voti per Forza Italia,azzerando il GAP con l'Unione prodiana).
Per farvi un esempio sul sito del ministero le regionali del Molise del 2011 risultano vinte dal CDX per 1500 voti.
Ma se cercate sulla rete vedrete che i giudici rifacendo i conti e proclamando il risultato hanno diminuito il vantaggio a 950.
(una differenza grande per una regione piccola)
Quindi il doppio controllo pone rimedio ad errori di trasmissione.
E questo fa cedere la ipotesi del broglio informatico.
C'è la possibilità del broglio ai seggi.
Che cioè il CDX abbia materialmente fatto il broglio nei seggi alterando il risultato.
Però è un'ipotesi assurda,se non altro nelle dimensioni.
Infatti vorrebbe dire che il CDX ha fatto questo broglio in tutte,ma proprio tutte le 60000 sezioni italiane.
Infatti Deaglio trova anomalo che la diminuzione delle bianche sia uniforme e netta in praticamente tutte le sezioni.
Però un broglio così capillare mi pare davvero impossibile da ipotizzare.
Richiederebbe una organizzazione molto grossa e che avrebbe dovuto riguardare non solo i rappresentanti di lista del PDL,
ma tutto il personale dei seggi,presidenti,vice,scrutatori e forze dell'ordine,nonchè i rappresentanti di lista del CSX.
Mi pare molto difficile.
Poi bisogna tenere conto di 2 fatti:
le bianche sono state alte a più di un milione solo nelle 3 votazioni col maggioritario del Matterellum,
prima col proporzionale puro erano molte meno,800-900000,al massimo,ma anche meno,400 o 500 mila.
Poi nel 2008 e nel 2013 col ministero non più in mano al CDX le bianche sono rimaste basse,485000 nel 2008 e 395000 nel 2013.
Se come implicava la teoria di Deaglio la quantità fisiologica di bianche con l'80% dei votanti è di un milione e mezzo
(trovando appunto anomalo che nel 2006 fossero solo 444000 e per questo ipotizzando i brogli)ecco allora che
nel 2008 e nel 2013 dovevano tornare a salire,invece si sono mantenute sullo stesso numero.
Nel 2006 il passaggio da 1700000 a 440000 bianche poteva far pensare,sembrare strano,ma oggi penso che
si possa ipotizzare che invece sia dovuto al cambio della legge elettorale,in quanto il Porcellum ha stimoli ed incentivi sull'elettore diversi dal Mattarellum.
La tesi del software che avrebbe dirottato le bianche su Forza Italia non regge.
Per il semplice fatto che i dati del sito del ministero non hanno valore legale ai fini della proclamazione del risultato vero e proprio.
Essa avviene tramite il riconteggio di tutti i verbali cartacei originali di tutte e 60000 le sezioni italiane,
che dopo essere stati scrutinati nel seggio confluiscono a Roma alla Corte di Cassazione che ricontandoli appunto
fa le somme dei partiti e delle coalizioni e proclama i risultati ufficiali e definitivi.
In questi verbali naturalmente ci sono anche le schede bianche segnate.
Ora,quando nel 2006 i giudici hanno fatto i conti il risultato che è uscito è stato davvero di 19 milioni a testa per le coalizioni e di solo 440000 schede bianche.
Se fosse come inizialmente diceva Deaglio,e cioè del dato del sito del ministero alterato,allora rifacendo i conti
sui verbali originali sarebbe dovuta uscire una grande differenza tra le coalizioni,cioè 19 per il CSX,ma meno di 18 per il CDX.
Perchè le bianche anzichè solo 440000 dovevano risultare più di un milione e mezzo.(la teoria appunto era che il CDX in un qualche modo le avesse trasformate in voti per Forza Italia,azzerando il GAP con l'Unione prodiana).
Per farvi un esempio sul sito del ministero le regionali del Molise del 2011 risultano vinte dal CDX per 1500 voti.
Ma se cercate sulla rete vedrete che i giudici rifacendo i conti e proclamando il risultato hanno diminuito il vantaggio a 950.
(una differenza grande per una regione piccola)
Quindi il doppio controllo pone rimedio ad errori di trasmissione.
E questo fa cedere la ipotesi del broglio informatico.
C'è la possibilità del broglio ai seggi.
Che cioè il CDX abbia materialmente fatto il broglio nei seggi alterando il risultato.
Però è un'ipotesi assurda,se non altro nelle dimensioni.
Infatti vorrebbe dire che il CDX ha fatto questo broglio in tutte,ma proprio tutte le 60000 sezioni italiane.
Infatti Deaglio trova anomalo che la diminuzione delle bianche sia uniforme e netta in praticamente tutte le sezioni.
Però un broglio così capillare mi pare davvero impossibile da ipotizzare.
Richiederebbe una organizzazione molto grossa e che avrebbe dovuto riguardare non solo i rappresentanti di lista del PDL,
ma tutto il personale dei seggi,presidenti,vice,scrutatori e forze dell'ordine,nonchè i rappresentanti di lista del CSX.
Mi pare molto difficile.
Poi bisogna tenere conto di 2 fatti:
le bianche sono state alte a più di un milione solo nelle 3 votazioni col maggioritario del Matterellum,
prima col proporzionale puro erano molte meno,800-900000,al massimo,ma anche meno,400 o 500 mila.
Poi nel 2008 e nel 2013 col ministero non più in mano al CDX le bianche sono rimaste basse,485000 nel 2008 e 395000 nel 2013.
Se come implicava la teoria di Deaglio la quantità fisiologica di bianche con l'80% dei votanti è di un milione e mezzo
(trovando appunto anomalo che nel 2006 fossero solo 444000 e per questo ipotizzando i brogli)ecco allora che
nel 2008 e nel 2013 dovevano tornare a salire,invece si sono mantenute sullo stesso numero.
Nel 2006 il passaggio da 1700000 a 440000 bianche poteva far pensare,sembrare strano,ma oggi penso che
si possa ipotizzare che invece sia dovuto al cambio della legge elettorale,in quanto il Porcellum ha stimoli ed incentivi sull'elettore diversi dal Mattarellum.
Ragazzi
sapendo che per qualcuno di voi l’argomento è veramente ‘stuzzicante’, non perdiamo tempo ed esaminiamo il voto ‘napoletano’ al Senato. Che la cosa non sia irrilevante lo si capisce dalle seguenti righe, tratte sempre dal già citato comunicato di Forza Italia…
Alla Camera le schede bianche sono 440.517 contro 1.707.269 del 2001, con un calo del 74,2%. Al Senato le schede bianche sono 479.214, contro 1.278.831 del 2001, con una diminuzione del 72,6%. Questi dati dimostrano che i nostri sospetti sulla regolarità del voto sono più che fondati. Infatti, il fatto che si registrino più schede bianche nelle elezioni del Senato [quasi 480mila…] rispetto alla Camera [440mila…] è un’anomalia pressoché impossibile da spiegare, visto che sono ben tre milioni e mezzo in più gli elettori della Camera dei deputati. Infatti occorrerebbe ipotizzare due eventi di probabilità pari a zero:
che nessuno tra i tre milioni e mezzo di elettori con meno di venticinque anni abbia votato scheda bianca
che 40mila elettori abbiano votato per la Camera e non per il Senato.
I dubbi si rivelano ancora più fondati se si considerano alcuni fatti significativi. Nelle votazioni per il Senato la regione decisiva è stata la Campania. Qui l’Unione avrebbe prevalso per circa 15mila voti [15.771] di differenza, ottenendo il 49,6% contro il 49,1% della CdL [1.507.646 voti contro 1.491.875]. Se la CdL avesse prevalso al Senato in Campania, poiché il premio di maggioranza in quella regione è di quattro senatori, oggi in Senato la maggioranza sarebbe della CdL. Le schede bianche al Senato in Campania sono state solo 52.093, contro 216.901 del 2001. Il calo è di circa il 76%. Scorporando il dato della Campania [dove gli elettori sono oltre tre milioni…] dal dato nazionale, la diminuzione di schede bianche a livello nazionale è del 60%. Se applichiamo questo dato statistico alla Campania, le schede bianche avrebbero dovuto essere non 52-mila, ma circa 84-mila. Ci sono cioè ben 32-mila schede bianche in meno rispetto alla fisiologica diminuzione delle schede bianche…
A napoli i votanti al Senato sono stati $520.119$ [circa $70.000$ in meno che alla Camera…] il che su $865$ sezioni significa circa $600$ elettori per sezione. A questo punto una primo fatto singolare [ma non tanto in fondo…]: anche se i votanti sono per il Senato sono in numero inferiore rispetto alla Camera, le schede bianche sono in numero maggiore. Le schede bianche al Senato sono infatti $3442$ contro le $3112$ della Camera… oltre $300$ in più!… Che i napoletani siano un poco ‘originali’ è cosa nota… ma che qualcuno di loro abbia votato ‘regolarmente’ alla Camera e scheda bianca al Senato è veramente ‘singolare’, non trovate?… o per caso c’entrano anche qui in qualche modo i Testimoni di Geova? …
…
Sia come sia al numero delle bianche corrisponde una probabilità $p=6.62*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 43
1 / 101
2 / 138
3 / 148
4 / 105
5 / 109
6 / 89
7 / 51
8 / 37
9 / 20
10 / 8
11 / 6
12 / 3
13 / 1
14 / 1
15 / 3
16 / 1
17 / 0
18 / 0
19 / 0
20 / 0
21 / 0
22 / 1
Il consueto digramma dati regolari/dati reali lo riportiamo subito…

Bene ragazzi!… la prima cosa che salta all’occhio è il valore ‘isolato’ con $k=22$… si tratta di nuovo della sezione $661$ [in località Ponticelli-San Giovanni]… solo che alla Camera era $k=18$… ah, questi Testimoni di Geova! …
…
La seconda cosa che salta all’occhio è che questa volta le ‘gobbe del cammello’ si vedono proprio bene! …
…
Amenità a parte i valori di media e varianza ‘reali’ sono…
$mu=3.98$
$sigma^2=7.05$ (1)
… mentre i valori ‘regolari’ sono…
$mu=n*p=3.97$
$sigma^2=n*p*(1-p)=3.94$ (2)
Media perfetta... varianza quasi il doppio… oh yes!!!… Per il vostro piacere ragazzi, vi comunico che in questo caso la soluzione ‘a minimo scarto quadratico’ e la soluzione ‘a miglior approssimazione di media e varianza’ in pratica coincidono e si hanno per i valori seguenti…
$eta=.444$
$p=1*10^(-2)$
$gamma=.42$ (3)
Il diagramma dati reali/modello è mostrato qui…

Lo scarto quadratico medio è pari a $7*10^(-3)$. Media e varianza sono invece…
$mu=4.06$
$sigma^2=7.02$ (4)
Nell’ipotesi che il modello sia ‘aderente alla realtà’, le schede bianche ‘napoletane’ al Senato dovevano essere in origine $n*p=5201$ e ne sono sopravvissute $3442$. Le schede desaparecidas sarebbero dunque $5201-3442=1759$… le buonanime di Lenin, Stalin e Pol Pot ‘benedicono’ gli ‘scugnizzi’ di Napoli!!! …
…
Bene ragazzi… ora abbiamo se non altro un’idea di quello che è accaduto un po’ dovunque nei seggi di Lazio e Campania in quella ‘sera maledetta’… è chiaro che averlo dimostrato è destinato a restare una soddisfazione puramente ‘accademica’ giacchè andare davanti a un giudice con motivazioni di questo tipo [e il processo per la strage di Ustica lo ha confermato…] servirebbe solo a tirarsi addosso sorrisi di compatimento… tutto quello che possiamo fare è ricordarci bene tutto questo in modo da ‘potersi regolare’ in futuro …
…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
sapendo che per qualcuno di voi l’argomento è veramente ‘stuzzicante’, non perdiamo tempo ed esaminiamo il voto ‘napoletano’ al Senato. Che la cosa non sia irrilevante lo si capisce dalle seguenti righe, tratte sempre dal già citato comunicato di Forza Italia…
Alla Camera le schede bianche sono 440.517 contro 1.707.269 del 2001, con un calo del 74,2%. Al Senato le schede bianche sono 479.214, contro 1.278.831 del 2001, con una diminuzione del 72,6%. Questi dati dimostrano che i nostri sospetti sulla regolarità del voto sono più che fondati. Infatti, il fatto che si registrino più schede bianche nelle elezioni del Senato [quasi 480mila…] rispetto alla Camera [440mila…] è un’anomalia pressoché impossibile da spiegare, visto che sono ben tre milioni e mezzo in più gli elettori della Camera dei deputati. Infatti occorrerebbe ipotizzare due eventi di probabilità pari a zero:
che nessuno tra i tre milioni e mezzo di elettori con meno di venticinque anni abbia votato scheda bianca
che 40mila elettori abbiano votato per la Camera e non per il Senato.
I dubbi si rivelano ancora più fondati se si considerano alcuni fatti significativi. Nelle votazioni per il Senato la regione decisiva è stata la Campania. Qui l’Unione avrebbe prevalso per circa 15mila voti [15.771] di differenza, ottenendo il 49,6% contro il 49,1% della CdL [1.507.646 voti contro 1.491.875]. Se la CdL avesse prevalso al Senato in Campania, poiché il premio di maggioranza in quella regione è di quattro senatori, oggi in Senato la maggioranza sarebbe della CdL. Le schede bianche al Senato in Campania sono state solo 52.093, contro 216.901 del 2001. Il calo è di circa il 76%. Scorporando il dato della Campania [dove gli elettori sono oltre tre milioni…] dal dato nazionale, la diminuzione di schede bianche a livello nazionale è del 60%. Se applichiamo questo dato statistico alla Campania, le schede bianche avrebbero dovuto essere non 52-mila, ma circa 84-mila. Ci sono cioè ben 32-mila schede bianche in meno rispetto alla fisiologica diminuzione delle schede bianche…
A napoli i votanti al Senato sono stati $520.119$ [circa $70.000$ in meno che alla Camera…] il che su $865$ sezioni significa circa $600$ elettori per sezione. A questo punto una primo fatto singolare [ma non tanto in fondo…]: anche se i votanti sono per il Senato sono in numero inferiore rispetto alla Camera, le schede bianche sono in numero maggiore. Le schede bianche al Senato sono infatti $3442$ contro le $3112$ della Camera… oltre $300$ in più!… Che i napoletani siano un poco ‘originali’ è cosa nota… ma che qualcuno di loro abbia votato ‘regolarmente’ alla Camera e scheda bianca al Senato è veramente ‘singolare’, non trovate?… o per caso c’entrano anche qui in qualche modo i Testimoni di Geova?
 …
… Sia come sia al numero delle bianche corrisponde una probabilità $p=6.62*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 43
1 / 101
2 / 138
3 / 148
4 / 105
5 / 109
6 / 89
7 / 51
8 / 37
9 / 20
10 / 8
11 / 6
12 / 3
13 / 1
14 / 1
15 / 3
16 / 1
17 / 0
18 / 0
19 / 0
20 / 0
21 / 0
22 / 1
Il consueto digramma dati regolari/dati reali lo riportiamo subito…

Bene ragazzi!… la prima cosa che salta all’occhio è il valore ‘isolato’ con $k=22$… si tratta di nuovo della sezione $661$ [in località Ponticelli-San Giovanni]… solo che alla Camera era $k=18$… ah, questi Testimoni di Geova!
 …
… La seconda cosa che salta all’occhio è che questa volta le ‘gobbe del cammello’ si vedono proprio bene!
 …
… Amenità a parte i valori di media e varianza ‘reali’ sono…
$mu=3.98$
$sigma^2=7.05$ (1)
… mentre i valori ‘regolari’ sono…
$mu=n*p=3.97$
$sigma^2=n*p*(1-p)=3.94$ (2)
Media perfetta... varianza quasi il doppio… oh yes!!!… Per il vostro piacere ragazzi, vi comunico che in questo caso la soluzione ‘a minimo scarto quadratico’ e la soluzione ‘a miglior approssimazione di media e varianza’ in pratica coincidono e si hanno per i valori seguenti…
$eta=.444$
$p=1*10^(-2)$
$gamma=.42$ (3)
Il diagramma dati reali/modello è mostrato qui…

Lo scarto quadratico medio è pari a $7*10^(-3)$. Media e varianza sono invece…
$mu=4.06$
$sigma^2=7.02$ (4)
Nell’ipotesi che il modello sia ‘aderente alla realtà’, le schede bianche ‘napoletane’ al Senato dovevano essere in origine $n*p=5201$ e ne sono sopravvissute $3442$. Le schede desaparecidas sarebbero dunque $5201-3442=1759$… le buonanime di Lenin, Stalin e Pol Pot ‘benedicono’ gli ‘scugnizzi’ di Napoli!!!
 …
… Bene ragazzi… ora abbiamo se non altro un’idea di quello che è accaduto un po’ dovunque nei seggi di Lazio e Campania in quella ‘sera maledetta’… è chiaro che averlo dimostrato è destinato a restare una soddisfazione puramente ‘accademica’ giacchè andare davanti a un giudice con motivazioni di questo tipo [e il processo per la strage di Ustica lo ha confermato…] servirebbe solo a tirarsi addosso sorrisi di compatimento… tutto quello che possiamo fare è ricordarci bene tutto questo in modo da ‘potersi regolare’ in futuro
 …
… cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Ragazzi
salutando dunque Marisa e ringraziandola per il suo prezioso contributo, vediamo di riprendere da dove eravamo rimasti…
A Napoli per la Camera dei deputati i votanti, distribuiti in $865$ sezioni, sono stati $590.506$, in media $682$ per sezione. Le schede bianche sono state in tutto $3122$, il che significa un tasso $p=5.27*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 59
1 / 115
2 / 155
3 / 149
4 / 129
5 / 95
6 / 63
7 / 36
8 / 26
9 / 16
10 / 5
11 / 6
12 / 1
13 / 2
14 / 3
15 / 3
16 / 0
17 / 0
18 / 2
Il grafico delle distribuzioni ‘regolare’ e ‘reale’ sono qui riportati in rosso e nero rispettivamente…

Media e varianza ‘reali’ sono…
$mu=3.61$
$sigma^2=6.77$ (1)
… a fronte di valori ‘regolari’ pari a …
$mu=n*p=4.56$
$sigma^2=n*p*(1-p)=4.53$ (2)
Dire che siamo di fronte ad una situazione ‘anomala’ non è certo ‘esagerato’!… per cercare di ‘decifrare’ la ‘anomalia’ usiamo la stessa tecnica impiegata per Roma, utilizzando il ‘modello dei postini’ basato sui tre parametri $eta$, $p$ e $gamma$. Arriviamo anche in questo caso a due ‘soluzioni’ che ora esaminiamo. La prima è ottenuta trovando i tre parametri che rendono minimo lo ‘scarto quadratico medio’ con i dati reali…
$eta=.55$
$p=6.79*10^(-3)$
$gamma=. 44$ (3)
Il diagramma ‘modello/dati reali’ è il seguente…

Lo scarto quadratico medio vale $4.3*10^(-3)$ e i valori di media e varianza associati sono…
$mu=3.47$
$sigma^2=5.1$ (4)
Se il modello fosse ‘reale’ il numero di schede bianche della Camera in tutta Napoli avrebbe dovuto essere $n*p=4009$. Dal momento che in realtà sono $3122$ le schede bianche desaparecidas sarebbero $4009-3122=887$… insomma non proprio ‘due o tre’ ecco…
Come si vede dalla figura tuttavia, restano ‘fuori’ dalla curva rossa un numero non proprio insignificante di sezioni in cui si sono avute $12$, $13$,$14$,$15$… e perfino $18$ schede bianche… E’ facile vedere poi che i valori di media e varianza (4) sono un poco lontani dai valori ‘reali’ e questo suggerisce che il quadro reale avutosi debba essere diverso. Esaminiamo così la seconda ‘soluzione’ , ottenuta trovando i valori dei parametri che meglio approssimano media e varianza ‘reali’…
$eta=.36$
$p=8.8*10^(-3)$
$gamma=. 4$ (5)
Il diagramma ‘modello/dati reali’ è il seguente…

Lo scarto quadratico medio vale $8.4*10^(-3)$ e i valori di media e varianza sono…
$mu=3.69$
$sigma^2=6.68$ (6)
Se il modello fosse ‘reale’ il numero di schede bianche ‘napoletane’ alla Camera avrebbe dovuto essere $n*p=5196$. Dal momento che in realtà sono $3122$ le schede desaparecidas in tal caso sarebbero $5196-3112=2074$… poco ci manca che non si siano dimezzate! …
…
Se ora osserviamo la figura notiamo che le due sezioni con $k=18$ sono ‘ancora’ fuori della curva rossa. Ciò significa che se cercassimo di ‘prenderle dentro’ potremmo scoprire un numero di schede bianche ‘assassinate’ semplicemente ‘incredibile’ … Onestamente a questo punto mi manca il ‘coraggio’ eseguire questa ulteriore ricerca [che tuttavia può essere fatta da uno di voi che voglia ‘cimentarsi’…] e preferisco prendere per buono quello che dice Marisa riguardo ai ‘Testimoni di Geova’
 …
…
… anche perchè ‘il bello’ deve ancora venire e riguarda l’analisi del voto ‘napoletano’ al Senato… per cui ragazzi… non perdete le prossime puntate! …
…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
salutando dunque Marisa e ringraziandola per il suo prezioso contributo, vediamo di riprendere da dove eravamo rimasti…
A Napoli per la Camera dei deputati i votanti, distribuiti in $865$ sezioni, sono stati $590.506$, in media $682$ per sezione. Le schede bianche sono state in tutto $3122$, il che significa un tasso $p=5.27*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 59
1 / 115
2 / 155
3 / 149
4 / 129
5 / 95
6 / 63
7 / 36
8 / 26
9 / 16
10 / 5
11 / 6
12 / 1
13 / 2
14 / 3
15 / 3
16 / 0
17 / 0
18 / 2
Il grafico delle distribuzioni ‘regolare’ e ‘reale’ sono qui riportati in rosso e nero rispettivamente…

Media e varianza ‘reali’ sono…
$mu=3.61$
$sigma^2=6.77$ (1)
… a fronte di valori ‘regolari’ pari a …
$mu=n*p=4.56$
$sigma^2=n*p*(1-p)=4.53$ (2)
Dire che siamo di fronte ad una situazione ‘anomala’ non è certo ‘esagerato’!… per cercare di ‘decifrare’ la ‘anomalia’ usiamo la stessa tecnica impiegata per Roma, utilizzando il ‘modello dei postini’ basato sui tre parametri $eta$, $p$ e $gamma$. Arriviamo anche in questo caso a due ‘soluzioni’ che ora esaminiamo. La prima è ottenuta trovando i tre parametri che rendono minimo lo ‘scarto quadratico medio’ con i dati reali…
$eta=.55$
$p=6.79*10^(-3)$
$gamma=. 44$ (3)
Il diagramma ‘modello/dati reali’ è il seguente…

Lo scarto quadratico medio vale $4.3*10^(-3)$ e i valori di media e varianza associati sono…
$mu=3.47$
$sigma^2=5.1$ (4)
Se il modello fosse ‘reale’ il numero di schede bianche della Camera in tutta Napoli avrebbe dovuto essere $n*p=4009$. Dal momento che in realtà sono $3122$ le schede bianche desaparecidas sarebbero $4009-3122=887$… insomma non proprio ‘due o tre’ ecco…
Come si vede dalla figura tuttavia, restano ‘fuori’ dalla curva rossa un numero non proprio insignificante di sezioni in cui si sono avute $12$, $13$,$14$,$15$… e perfino $18$ schede bianche… E’ facile vedere poi che i valori di media e varianza (4) sono un poco lontani dai valori ‘reali’ e questo suggerisce che il quadro reale avutosi debba essere diverso. Esaminiamo così la seconda ‘soluzione’ , ottenuta trovando i valori dei parametri che meglio approssimano media e varianza ‘reali’…
$eta=.36$
$p=8.8*10^(-3)$
$gamma=. 4$ (5)
Il diagramma ‘modello/dati reali’ è il seguente…

Lo scarto quadratico medio vale $8.4*10^(-3)$ e i valori di media e varianza sono…
$mu=3.69$
$sigma^2=6.68$ (6)
Se il modello fosse ‘reale’ il numero di schede bianche ‘napoletane’ alla Camera avrebbe dovuto essere $n*p=5196$. Dal momento che in realtà sono $3122$ le schede desaparecidas in tal caso sarebbero $5196-3112=2074$… poco ci manca che non si siano dimezzate!
 …
… Se ora osserviamo la figura notiamo che le due sezioni con $k=18$ sono ‘ancora’ fuori della curva rossa. Ciò significa che se cercassimo di ‘prenderle dentro’ potremmo scoprire un numero di schede bianche ‘assassinate’ semplicemente ‘incredibile’ … Onestamente a questo punto mi manca il ‘coraggio’ eseguire questa ulteriore ricerca [che tuttavia può essere fatta da uno di voi che voglia ‘cimentarsi’…] e preferisco prendere per buono quello che dice Marisa riguardo ai ‘Testimoni di Geova’

 …
… … anche perchè ‘il bello’ deve ancora venire e riguarda l’analisi del voto ‘napoletano’ al Senato… per cui ragazzi… non perdete le prossime puntate!
 …
… cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Ragazzi
che vi devo dire?… Quello che so della ‘faccenda Deaglio’ è ciò che ho letto sui giornali e che si può riassumere in questo…
All’indomani della ‘presentazione’ del film ‘Uccidete la Democrazia!’ la procura di Roma ha aperto un fascicolo di indagine sulla base delle ‘rivelazioni’ di Deaglio. E’ stato in primo luogo sentito come testimone un funzionario del ministero degli interni al tempo delle elezioni il quale ha dichiarato che il ‘software’ in questione aveva unicamente funzione divulgativa ‘in anteprima’ dei risultati ed era ininfluente nei confronti della procedura di controllo dei risultati da parte delle corti d’appello. Queste ultime infatti hanno ‘verificato’ i risultati sulla base dei verbali delle sezioni i quali a loro volta si basavano sulle schede elettorali conservate nelle prefetture. Tutto ‘materiale cartaceo’ insomma e se vi fosse stata una qualche ‘manipolazione’ dei risultati da parte del ministero questa sarebbe emersa in poco tempo. Tale testimonianza è bastata da sola ampiamente a ‘demolire’ la ‘tesi’ di Deaglio e la procura di Roma altro non ha potuto fare che ‘incriminarlo’ per calunnia…
Del resto è ovvio in base al più elementare buon senso che se i dati elettorali sono interamente ‘scritti su carta’ [schede e verbali…] è difficile immaginare un ‘software’ in grado di ‘manipolarli’, operazione alla quale si prestano invece egregiamente gli ‘accessori’ che vedete qui sotto
 …
…

Ciò detto ‘per amore di cronaca’, riterrei opportuno procedere nella analisi da me intrapresa lasciando al ‘mitico Deaglio’ il compito piacevole di ‘convincere’ il giudice del tribunale della sua ‘innocenza’ …
…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
che vi devo dire?… Quello che so della ‘faccenda Deaglio’ è ciò che ho letto sui giornali e che si può riassumere in questo…
All’indomani della ‘presentazione’ del film ‘Uccidete la Democrazia!’ la procura di Roma ha aperto un fascicolo di indagine sulla base delle ‘rivelazioni’ di Deaglio. E’ stato in primo luogo sentito come testimone un funzionario del ministero degli interni al tempo delle elezioni il quale ha dichiarato che il ‘software’ in questione aveva unicamente funzione divulgativa ‘in anteprima’ dei risultati ed era ininfluente nei confronti della procedura di controllo dei risultati da parte delle corti d’appello. Queste ultime infatti hanno ‘verificato’ i risultati sulla base dei verbali delle sezioni i quali a loro volta si basavano sulle schede elettorali conservate nelle prefetture. Tutto ‘materiale cartaceo’ insomma e se vi fosse stata una qualche ‘manipolazione’ dei risultati da parte del ministero questa sarebbe emersa in poco tempo. Tale testimonianza è bastata da sola ampiamente a ‘demolire’ la ‘tesi’ di Deaglio e la procura di Roma altro non ha potuto fare che ‘incriminarlo’ per calunnia…
Del resto è ovvio in base al più elementare buon senso che se i dati elettorali sono interamente ‘scritti su carta’ [schede e verbali…] è difficile immaginare un ‘software’ in grado di ‘manipolarli’, operazione alla quale si prestano invece egregiamente gli ‘accessori’ che vedete qui sotto

 …
… Ciò detto ‘per amore di cronaca’, riterrei opportuno procedere nella analisi da me intrapresa lasciando al ‘mitico Deaglio’ il compito piacevole di ‘convincere’ il giudice del tribunale della sua ‘innocenza’
 …
… cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Tale ‘film’ [il cui ‘successo’ conseguito in termini di audience mi è del tutto sconosciuto…] verte intorno alla seguente ‘trama’: il ministero degli interni avrebbe nella circostanza, tramite un rocambolesco software importato dagli Usa, ‘trasformato’ un gran numero di schede ‘bianche’ in voti validi. Come ben si sa l’assoluta inconsistenza di tale ‘trama’ è apparsa subito evidente, al punto che il ‘giornalista’ in questione è stato rinviato a giudizio con l’accusa di calunnia. A parte però le ‘tesi’ più o meno demenziali di costui, che cosa si può dire della presunta ‘metamorfosi’ delle schede?
Ciao Lupo grigio,stavo stampando il tuo lavoro quando mi sono accorta di queste righe purtroppo ti ho detto che mi ero concessa delle ferie e che leggevo un po’ sommariamente e per considerare le cose mi è necessario stampare.
Mi dispiace non aver reagito nel modo appropriato all’inizio.
Il film ha avuto una grande audience e continua ad essere scaricato gratuitamente da arcoiris,nessuno ha mai affermato che sia stato il Ministero dell’interno a inserire un software “avariato” nella rete,né che l’abbia acquistato in Usa perché sarebbe stato ridicolo andare fin là(Clinton Curtis ha solo dimostrato che costruirlo è un gioco da bambini e che può realizzarlo anche un principiante,non capisco perché lo definisci “rocambolesco”)
Dire che la trama è inconsistente è come credere alla “Befana”…
Quello però che trovo inappropriato per uno che si interessa di matematica e quindi cerca di interpretare la realtà e deve farlo con l’aiuto senz’altro di persone che l’hanno preceduto nel campo e di altre che lo attorniano ,sono gli insulti gratuiti.
Che ne diresti se io senza conoscerti ti definissi”matematico” e ti giudicassi in base a ciò che ricavo dai tuoi scritti in base alle mie possibilità mentali più o meno estese ma sempre estremamente limitate rispetto alla vera conoscenza e soggette all’errore?
Deaglio non è stato rinviato a giudizio per calunnia ma per una legge del tempo del fascismo,usata una sola volta,pare, nei confronti di Tina Merlin una giornalista che informò dei pericoli della diga del Vayont e che venne messa a tacere per coprire enormi interessi,dopo tre anni la diga saltò e provocò molte vittime
La magistratura dovrebbe evitare i giudizi frettolosi e privi di basi che danneggiano il singolo che porta alla luce fatti ignomignosi(ruberie,corruzione etc) nei confronti di uno Stato che non ne ha più le parvenze purtroppo;prima di accusare qualcuno ci si documenta,questo ha bisogno di tempo(non 15 giorni comprese le vacanze di Natale)e lo si fa con prove ben motivate ,nessun lavoro permettere di superare il diritto o di essere superficiali danneggiando alcuni per proteggere altri.
Quanto alle “tesi più o meno demenziali” io credo che le offese ritornino su chi le lancia perché sbagliare possiamo tutti ma non offendere gli altri soprattutto quando riferiscono solo ciò che è successo e portano dati validi:considerare prova irrilevante un appiattimento omogeneo delle schede bianche in tutta Italia (in Campania si scende addirittura al 17%)mi sembra ,per un matematico, un pochino azzardato soprattutto se a questo si affiancano molte altre stranezze.
Nell’ultimo film “Gli imbroglioni” è stato dimostrato che la sicurezza era affidata agli spioni di telecom ,almeno tre blocchi prolungati del sistema si sono succeduti, valori sono variati dalla partenza all’arrivo testimoniando la presenza di un intervento estraneo e i magistrati di appello non controllano effettivamente quale sia la natura e il contenuto del verbale tanto è vero che verbali non regolamentari(privi di timbri e firme o assurdi come contenuti) vengono convalidati(questo anche per mia esperienza).
Ultimamente ho anche trovato che a Caserta c’è stato un blocco di 1 ora e mezza che in effetti si è poi protratto per 6 prima che si potesse disporre dei dati finali e il prefetto ha ammesso che il tutto era stato dovuto a un errore del programma che attribuiva voti di alcuni partiti ad altri partiti,non si sa che cosa abbiano fatto di questo programma invece che consegnarlo alle autorità.
Sinceramente la tua premessa mi ha offeso perché per principio discuto con chi rispetta ciò che l’altro dice e non usa termini come “demenziale” ,se si hanno prove contrarie si riferiscono e l’altro risponde e si cerca di venirne obiettivamente a capo,chi ha ragione non ha bisogno di intaccare la dignità altrui.
Ho visto anche la tua ultima osservazione in blu....povero motore azzurro coi suoi 180mila legionari (e scrutatori eletti prima che scadessero i termini non comunicati agli altri) si sono trovati in difficoltà?Mi dispiace!
Pur non essendo un’esperta, mi sarebbe piaciuto entrare in merito alla faccenda e discuterne con te,ho fatto dei lavori che richiedevano l’uso di calcoli statistici per valutare la fondatezza di risultati e volentieri avrei speso un po’ di tempo per rivedere le cose che non ho più presenti,detto ciò senza rancore ti saluto ma ,considerato anche i vari “chimici”, penso che debba considerare out questo forum,un saluto.
Ragazzi
eccomi di nuovo a voi!… prima di proseguire il nostro discorso non sarà male riportare alcune righe di un comunicato rilasciato da Forza Italia alcune settimane dopo le elezioni che può essere assai ‘illuminante’ sul tema che stiamo trattando…
Accanto a queste considerazioni statistiche c’è una considerazione di fatto, di natura politica. Nella notte del 10 aprile, intorno alle 21:00, mentre lo scrutinio era ancora in corso, il coordinamento dell’Ulivo invitò ‘i parlamentari di Lazio e Campania a esercitare la massima vigilanza presso le prefetture per ristabilire il regolare andamento delle procedure di scrutinio’. Fu un avvertimento inaccettabile che in quel verbo [ristabilire] rivela quello che quei parlamentari, e i militanti che erano ai seggi sia come rappresentanti di lista che come scrutatori [gli scrutatori vengono scelti dai comuni, a grande maggioranza di sinistra…] avrebbero dovuto fare: assicurare con ogni mezzo, il successo dell’Unione alle elezioni.
Se si tiene conto del fatto che la CdL aveva rappresentanti di lista per meno della metà dei seggi, è possibile che in quelle ore nei seggi si possano essere verificate irregolarità. In Campania, dove le sezioni sono 5.736, sarebbe stato sufficiente trasformare in valide tre o quattro schede bianche per seggio per ottenere il risultato ottenuto. Analogamente, per la Camera, dove la differenza a livello nazionale è di sole 24-mila schede e le sezioni elettorali sono 60-mila, sarebbe bastata una scheda ogni tre sezioni…
Lazio e Campania dunque… al Lazio abbiamo già dato un’occhiata e una vaga idea di come sono andate le cose ce la siamo fatta… e per la Campania?… beh, ora che sappiamo come fare, non resta che andare a cercare un poco di dati sullo spogli elettorali in alcune sezioni della Campania e saremo in grado di immaginare che cosa è successo. Con un poco di pazienza sono andato a cercare nel sito del Comune di Napoli [ http://sre.comune.napoli.it/ ] e lì ho avuto la fortuna di trovare i risultati dello spoglio elettorale per la Camera e il Senato sezione per sezione su due fogli Excel… che naturalmente mi sono affrettato a scaricare…
Delle $886$ sezioni di Napoli ho deciso di scartare quelle con basso numero di votanti [ospedali, conventi, ricoveri per anziani e similari…] e i dati si riferiscono a sole $865$ sezioni. Per la Camera dei deputati i votanti in queste sezioni sono stati $590.506$, in media $682$ per sezione. Le schede bianche sono state in tutto $3122$, il che significa un tasso $p=5.27*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 59
1 / 115
2 / 155
3 / 149
4 / 129
5 / 95
6 / 63
7 / 36
8 / 26
9 / 16
10 / 5
11 / 6
12 / 1
13 / 2
14 / 3
15 / 3
16 / 0
17 / 0
18 / 2
Bene ragazzi, osserviamo subito il grafico…

Perdindirindina ragazzi!… se ben vi ricordate nel caso di Roma ci eravamo meravigliati che su $2600$ sezioni con una media di $2$ schede bianche a sezione vi fosse una sezione con $18$ schede bianche… ebbene qui a Napoli, con un numero di sezioni tre volte inferiore, le sezioni con $18$ schede bianche sono due e precisamente la sezione $490$ [in località Bagnoli-Fuorigrotta] e la sezione $661$ [in località Ponticelli-San Giovanni]… saranno anche qui i Testimoni di Geova?…
A parte le battute di spirito, andiamo a derivare subito media è varianza. Abbiamo…
$mu=3.61$
$sigma^2=6.77$ (1)
Se andiamo a calcolare quanto avrebbero dovuto essere in situazione ‘regolare’ otteniamo…
$mu=n*p=4.56$
$sigma^2=n*p*(1-p)=4.53$ (2)
Entrambe sono completamente sballate e già questo è forte indice di situazione ‘anomala’. Se poi osserviamo con attenzione la figura, con la curva in rosso corrispondente alla distribuzione ‘regolare’ e l’istogramma in nero della distribuzione ‘reale’, notiamo subito la presenza delle due ‘gobbe di cammello’ che comparivano nel 'diagramma dei postini’. Solo che in questo caso la gobba dei postini ‘onesti’ è quasi inesistente, mentre la gobba dei postini 'disonesti' è fin esagerata. Anche in assenza di una precisa analisi possiamo subito affermare di essere in presenza di una truffa di grosse dimensioni. Naturalmente la precisa analisi verrà fatta quanto prima… in attesa mi piacerebbe tanto sentire il parere di qualcuno…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
eccomi di nuovo a voi!… prima di proseguire il nostro discorso non sarà male riportare alcune righe di un comunicato rilasciato da Forza Italia alcune settimane dopo le elezioni che può essere assai ‘illuminante’ sul tema che stiamo trattando…
Accanto a queste considerazioni statistiche c’è una considerazione di fatto, di natura politica. Nella notte del 10 aprile, intorno alle 21:00, mentre lo scrutinio era ancora in corso, il coordinamento dell’Ulivo invitò ‘i parlamentari di Lazio e Campania a esercitare la massima vigilanza presso le prefetture per ristabilire il regolare andamento delle procedure di scrutinio’. Fu un avvertimento inaccettabile che in quel verbo [ristabilire] rivela quello che quei parlamentari, e i militanti che erano ai seggi sia come rappresentanti di lista che come scrutatori [gli scrutatori vengono scelti dai comuni, a grande maggioranza di sinistra…] avrebbero dovuto fare: assicurare con ogni mezzo, il successo dell’Unione alle elezioni.
Se si tiene conto del fatto che la CdL aveva rappresentanti di lista per meno della metà dei seggi, è possibile che in quelle ore nei seggi si possano essere verificate irregolarità. In Campania, dove le sezioni sono 5.736, sarebbe stato sufficiente trasformare in valide tre o quattro schede bianche per seggio per ottenere il risultato ottenuto. Analogamente, per la Camera, dove la differenza a livello nazionale è di sole 24-mila schede e le sezioni elettorali sono 60-mila, sarebbe bastata una scheda ogni tre sezioni…
Lazio e Campania dunque… al Lazio abbiamo già dato un’occhiata e una vaga idea di come sono andate le cose ce la siamo fatta… e per la Campania?… beh, ora che sappiamo come fare, non resta che andare a cercare un poco di dati sullo spogli elettorali in alcune sezioni della Campania e saremo in grado di immaginare che cosa è successo. Con un poco di pazienza sono andato a cercare nel sito del Comune di Napoli [ http://sre.comune.napoli.it/ ] e lì ho avuto la fortuna di trovare i risultati dello spoglio elettorale per la Camera e il Senato sezione per sezione su due fogli Excel… che naturalmente mi sono affrettato a scaricare…
Delle $886$ sezioni di Napoli ho deciso di scartare quelle con basso numero di votanti [ospedali, conventi, ricoveri per anziani e similari…] e i dati si riferiscono a sole $865$ sezioni. Per la Camera dei deputati i votanti in queste sezioni sono stati $590.506$, in media $682$ per sezione. Le schede bianche sono state in tutto $3122$, il che significa un tasso $p=5.27*10^(-3)$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 59
1 / 115
2 / 155
3 / 149
4 / 129
5 / 95
6 / 63
7 / 36
8 / 26
9 / 16
10 / 5
11 / 6
12 / 1
13 / 2
14 / 3
15 / 3
16 / 0
17 / 0
18 / 2
Bene ragazzi, osserviamo subito il grafico…

Perdindirindina ragazzi!… se ben vi ricordate nel caso di Roma ci eravamo meravigliati che su $2600$ sezioni con una media di $2$ schede bianche a sezione vi fosse una sezione con $18$ schede bianche… ebbene qui a Napoli, con un numero di sezioni tre volte inferiore, le sezioni con $18$ schede bianche sono due e precisamente la sezione $490$ [in località Bagnoli-Fuorigrotta] e la sezione $661$ [in località Ponticelli-San Giovanni]… saranno anche qui i Testimoni di Geova?…

A parte le battute di spirito, andiamo a derivare subito media è varianza. Abbiamo…
$mu=3.61$
$sigma^2=6.77$ (1)
Se andiamo a calcolare quanto avrebbero dovuto essere in situazione ‘regolare’ otteniamo…
$mu=n*p=4.56$
$sigma^2=n*p*(1-p)=4.53$ (2)
Entrambe sono completamente sballate e già questo è forte indice di situazione ‘anomala’. Se poi osserviamo con attenzione la figura, con la curva in rosso corrispondente alla distribuzione ‘regolare’ e l’istogramma in nero della distribuzione ‘reale’, notiamo subito la presenza delle due ‘gobbe di cammello’ che comparivano nel 'diagramma dei postini’. Solo che in questo caso la gobba dei postini ‘onesti’ è quasi inesistente, mentre la gobba dei postini 'disonesti' è fin esagerata. Anche in assenza di una precisa analisi possiamo subito affermare di essere in presenza di una truffa di grosse dimensioni. Naturalmente la precisa analisi verrà fatta quanto prima… in attesa mi piacerebbe tanto sentire il parere di qualcuno…

cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
In attesa di considerare meglio quello che dici.....la sezione a 17 schede bianche è la 344 di via Flavio Andò (non so che zona sia) ha (mi sembra) 860 votanti quindi nemmeno delle più grandi,potrebbero esserci testimoni di Geova o altro però anche solo 2-3 famiglie di T.G in una sezione dovrebbero portar su il valore di schede bianche(loro che sappia votano bianco)e in tutta Roma questa è la sola a fornire un simile valore.
Comunque per me anche quando l'appiattimento è provocato a livello centrale dovrebbe rimanere un segno....
Il range dei valori schede bianche per me dovrebbe essere più vasto di questo...
Un saluto.
Comunque per me anche quando l'appiattimento è provocato a livello centrale dovrebbe rimanere un segno....
Il range dei valori schede bianche per me dovrebbe essere più vasto di questo...
Un saluto.
cara Marisa
la tua osservazione è assai acuta e in effetti mi consente di mettere in chiaro un punto essenziale. Rifacendosi ancora all'esempio figurato dei postini di Manolestlanka, l'eventuale 'sparizione' di lettere contenenti denaro può essere dimostrata solo se essa è avvenuta in modo statisticamente anomalo. In pratica se alcuni postini sono 'onesti' e altri 'disonesti' allora si produce la 'dispersione statistica' che smaschera il fenomeno, vi sarà cioè un numero eccessivo di postini che hanno recapitato un numero lettere contenenti denaro 'lontano' [in più o in meno...] dal 'numero medio'. Se viceversa tutti i postini sono 'disonesti' non si registra alcuna 'anomalia statistica' e non è possibile dimostrare nulla. Accade lo stesso [cioè non è rilevabile con metodi statistici...] se l'eventuale 'sparizione' di lettere contenenti denaro fosse avvenuta in maniera cumulativa 'a monte', ad esempio da parte degli impiegati dell'ufficio postale di Manolestlanka e il perchè è del tutto evidente...
Detto questo torniamo un momento ai dati della circoscrizione di Roma e all'ultimo diagramma da me ottenuto...

Si è detto che i valor medio e la varianza della curva in rosso [$mu=3.24$ e $sigma^2=4.71$...] sono 'i più aderenti' alla realtà e ciò dovrebbe indurre a ritenere la curva relativamente 'verosimile'. Anche così tuttavia rimane un piccolo 'neo', costituito dal valore 'isolato' che si ha per $k=17$. Ossia in una sezione si è avuto un numero di schede bianche veramente 'anomalo'. In un caso del genere probabilmente la cosa migliore è andare a vedere di che sezione si tratta e magari a quel punto la 'spiegazione' della 'anomalia' diverrebbe evidente...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
la tua osservazione è assai acuta e in effetti mi consente di mettere in chiaro un punto essenziale. Rifacendosi ancora all'esempio figurato dei postini di Manolestlanka, l'eventuale 'sparizione' di lettere contenenti denaro può essere dimostrata solo se essa è avvenuta in modo statisticamente anomalo. In pratica se alcuni postini sono 'onesti' e altri 'disonesti' allora si produce la 'dispersione statistica' che smaschera il fenomeno, vi sarà cioè un numero eccessivo di postini che hanno recapitato un numero lettere contenenti denaro 'lontano' [in più o in meno...] dal 'numero medio'. Se viceversa tutti i postini sono 'disonesti' non si registra alcuna 'anomalia statistica' e non è possibile dimostrare nulla. Accade lo stesso [cioè non è rilevabile con metodi statistici...] se l'eventuale 'sparizione' di lettere contenenti denaro fosse avvenuta in maniera cumulativa 'a monte', ad esempio da parte degli impiegati dell'ufficio postale di Manolestlanka e il perchè è del tutto evidente...
Detto questo torniamo un momento ai dati della circoscrizione di Roma e all'ultimo diagramma da me ottenuto...

Si è detto che i valor medio e la varianza della curva in rosso [$mu=3.24$ e $sigma^2=4.71$...] sono 'i più aderenti' alla realtà e ciò dovrebbe indurre a ritenere la curva relativamente 'verosimile'. Anche così tuttavia rimane un piccolo 'neo', costituito dal valore 'isolato' che si ha per $k=17$. Ossia in una sezione si è avuto un numero di schede bianche veramente 'anomalo'. In un caso del genere probabilmente la cosa migliore è andare a vedere di che sezione si tratta e magari a quel punto la 'spiegazione' della 'anomalia' diverrebbe evidente...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Ciao L.G. appena posso stampo il tuo lavoro e cerco di capire approfonditamente,vorrei però farti una domanda ,visto che l'argomento mi interessa veramente:
"Potresti escludere che questa perdita più o meno ingente di cui parli possa essere l'ultimo stadio di un processo e quindi la situazione reale di partenza(il numero reale delle schede bianche)possa essere diversa da quella che qui proponi?"
Mi piacerebbe visto che sei così abile nel calcolo che te ne occupassi sul serio....per fini generali ma, secondo me, si dovrebbero considerare ulteriori elementi.
Un saluto.
"Potresti escludere che questa perdita più o meno ingente di cui parli possa essere l'ultimo stadio di un processo e quindi la situazione reale di partenza(il numero reale delle schede bianche)possa essere diversa da quella che qui proponi?"
Mi piacerebbe visto che sei così abile nel calcolo che te ne occupassi sul serio....per fini generali ma, secondo me, si dovrebbero considerare ulteriori elementi.
Un saluto.
Ragazzi
lasciando perdere gli 'scienziati nazi' e i loro calcoli sul 'volume del cervello' [ ], dal momento che so che più di uno di voi è ‘curioso’ di conoscere i risultati della mia ‘indagine’, eccomi di nuovo qui!… Per prima cosa ricapitoliamo i risultati…
], dal momento che so che più di uno di voi è ‘curioso’ di conoscere i risultati della mia ‘indagine’, eccomi di nuovo qui!… Per prima cosa ricapitoliamo i risultati…
Il dato di partenza è costituito dalla distribuzione delle schede bianche avutasi nella circoscrizione di Roma in occasione delle ultime elezioni politiche, rappresentata dall’istogramma in nero nella figura…

Detto $k$ l’intero che compare sull’asse delle ascisse si ha che la media e varianza di $k$ sono…
$E[k]=mu=3.209$
$E[(k-mu)^2]= sigma^2=4.79$ (1)
Se il diagramma rappresentasse una situazione ‘regolare’, essendo $n=700$ il numero medio di votanti per sezione e $p= 8344/1823836= .00457497…$ la percentuale cumulativa delle schede bianche, si dovrebbero riscontrare i seguenti valori…
$mu=n*p=3.22$
$sigma^2= n*p*(1-p)=3.18$ (2)
Il valore della media trovato è abbastanza ‘ragionevole’ , il valore della varianza dei dati ‘reali’ è eccessivo e ciò rende i dati stessi ‘statisticamente incoerenti’. Per giustificare l’evidente incongruenza dei dati si è fatta l’ipotesi che alcune schede bianche siano ‘scomparse’ in alcune sezioni ‘disoneste’ e abbiamo introdotto tre parametri ‘incogniti’ vale a dire…
$p$: tasso ‘reale’ di schede bianche in rapporto ai votanti
$eta$: tasso di ‘sezioni oneste’, cioè sezioni in cui non si è avuta ‘scomparsa’ di schede bianche
$gamma$: tasso di sopravvivenza delle schede bianche nelle sezioni ‘disoneste’
In tal caso la distribuzione statistica si calcola con la seguente formula…
$P_(n,k)= ((n),(k))* [eta*p^k*(1-p)^(n-k)+(1-eta)*(gamma*p)^k*(1-gamma*p)^(n-k)]$ (3)
La ricerca di $p$,$eta$ e $gamma$ è fatta cercando i valori dei tre parametri che minimizzano lo scarto quadratico tra la distribuzione ricavata con la (3) e la distribuzione realmente avutasi. Una prima ricerca da me fatta in modo piuttosto frettoloso ieri pomeriggio [dopo aver impiegato molto tempo per la stesura di un programma su PC atto allo scopo…] ha fornito i parametri seguenti…
$eta=.88$
$p=4.73*10^(-3)$
$gamma=.225$ (4)
… con valore di m.s.e. pari a $6.8*10^(-3)$. La curva di distribuzione con i parametri (4) è illustrata in figura…

I valori di media e varianza calcolati sono i seguenti…
$mu=3.01$
$sigma^2=3.7$ (5)
Rispetto alla curva normale il valor medio ha uno scarto maggiore ma in compenso il valore della varianza approssima assai meglio il valore ‘reale’, anche se è ancora ben lontano. Il risultato ancora non è soddisfacente perchè, a prescindere dalla scarsa precisione dei valori di $mu$ e $sigma^2$, nel diagramma è evidente la discrepanza con i valori ‘reali’ rilevati per $k>7$. Completando la ricerca con maggiore ‘attenzione’ si è riusciti a ottenere una ‘soluzione’ con scarto quadratico medio inferiore. La soluzione è la seguente…
$eta=.513$
$p=6*10^(-3)$
$gamma=.5$ (6)
...con valore di m.s.e. pari a $5.5*10^(-3)$. La curva di distribuzione con i parametri (6) è mostrata il figura…

I valori di media e varianza sono i seguenti…
$mu=3.17$
$sigma^2=4.26$ (7)
I valori (7) sono assai più vicini ai valori ‘reali’ di quanto non lo siano i valori (5) per cui la soluzione (6) è certamente più ‘verosimile’ rispetto alla (4) e la cosa appare del tutto evidente osservando il grafico. Nell’ipotesi che la soluzione ora trovata sia quella ‘giusta’, calcoliamo quante debbono essere state le schede bianche 'desaparecidas’. Se le schede sono state in totale $1.793.446$, ad una valore $p=6*10^(-3)$ corrispondono $10.760$ ‘schede bianche’. Siccome le schede bianche ‘reali’ sono state in tutto $8.344$ le schede bianche 'desaparecidas sono $10.760-8.344=2.416$. In tal caso, dal momento che il risultato è stato deciso da una differenza di $24.000$ voti, $2416$ ‘schede manipolate’ nella sola Roma non rappresentano una entità ‘trascurabile’…
La soluzione ora descritta è stata ottenuta con criterio della ‘minimizzazione dello scarto quadratico’. Un altro criterio ‘accettabile’ è quello di cercare di minimizzare lo scarto nei valori di $mu$ e $sigma^2$. La ricerca eseguita con questo criterio ha fornito la soluzione seguente…
$eta=.4644$
$p=6.5*10^(-3)$
$gamma=. 46$ (8)
… con valore m.s.e. pari a $6.7*10^(-3)$. La curva di distribuzione con i parametri (8) è mostrata in figura…

I valori di media e varianza sono i seguenti…
$mu=3.24$
$sigma^2=4.71$ (9)
Nell’ipotesi che questa sia la soluzione ‘giusta’ la stima delle schede bianche 'desaparecidas', eseguita con metodo usato prima, fornisce un valore pari a $3.313$, maggiore dunque rispetto al valore trovato in precedenza e per questo ancora meno ‘trascurabile’ nel determinare il risultato del voto nazionale…
Questi i risultati dell’analisi. In attesa dei ‘commenti’ vostri [che sinceramente sono curioso di sentire
 …] sono lieto di porgere a tutti i miei più…
…] sono lieto di porgere a tutti i miei più…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
lasciando perdere gli 'scienziati nazi' e i loro calcoli sul 'volume del cervello' [
 ], dal momento che so che più di uno di voi è ‘curioso’ di conoscere i risultati della mia ‘indagine’, eccomi di nuovo qui!… Per prima cosa ricapitoliamo i risultati…
], dal momento che so che più di uno di voi è ‘curioso’ di conoscere i risultati della mia ‘indagine’, eccomi di nuovo qui!… Per prima cosa ricapitoliamo i risultati… Il dato di partenza è costituito dalla distribuzione delle schede bianche avutasi nella circoscrizione di Roma in occasione delle ultime elezioni politiche, rappresentata dall’istogramma in nero nella figura…

Detto $k$ l’intero che compare sull’asse delle ascisse si ha che la media e varianza di $k$ sono…
$E[k]=mu=3.209$
$E[(k-mu)^2]= sigma^2=4.79$ (1)
Se il diagramma rappresentasse una situazione ‘regolare’, essendo $n=700$ il numero medio di votanti per sezione e $p= 8344/1823836= .00457497…$ la percentuale cumulativa delle schede bianche, si dovrebbero riscontrare i seguenti valori…
$mu=n*p=3.22$
$sigma^2= n*p*(1-p)=3.18$ (2)
Il valore della media trovato è abbastanza ‘ragionevole’ , il valore della varianza dei dati ‘reali’ è eccessivo e ciò rende i dati stessi ‘statisticamente incoerenti’. Per giustificare l’evidente incongruenza dei dati si è fatta l’ipotesi che alcune schede bianche siano ‘scomparse’ in alcune sezioni ‘disoneste’ e abbiamo introdotto tre parametri ‘incogniti’ vale a dire…
$p$: tasso ‘reale’ di schede bianche in rapporto ai votanti
$eta$: tasso di ‘sezioni oneste’, cioè sezioni in cui non si è avuta ‘scomparsa’ di schede bianche
$gamma$: tasso di sopravvivenza delle schede bianche nelle sezioni ‘disoneste’
In tal caso la distribuzione statistica si calcola con la seguente formula…
$P_(n,k)= ((n),(k))* [eta*p^k*(1-p)^(n-k)+(1-eta)*(gamma*p)^k*(1-gamma*p)^(n-k)]$ (3)
La ricerca di $p$,$eta$ e $gamma$ è fatta cercando i valori dei tre parametri che minimizzano lo scarto quadratico tra la distribuzione ricavata con la (3) e la distribuzione realmente avutasi. Una prima ricerca da me fatta in modo piuttosto frettoloso ieri pomeriggio [dopo aver impiegato molto tempo per la stesura di un programma su PC atto allo scopo…] ha fornito i parametri seguenti…
$eta=.88$
$p=4.73*10^(-3)$
$gamma=.225$ (4)
… con valore di m.s.e. pari a $6.8*10^(-3)$. La curva di distribuzione con i parametri (4) è illustrata in figura…

I valori di media e varianza calcolati sono i seguenti…
$mu=3.01$
$sigma^2=3.7$ (5)
Rispetto alla curva normale il valor medio ha uno scarto maggiore ma in compenso il valore della varianza approssima assai meglio il valore ‘reale’, anche se è ancora ben lontano. Il risultato ancora non è soddisfacente perchè, a prescindere dalla scarsa precisione dei valori di $mu$ e $sigma^2$, nel diagramma è evidente la discrepanza con i valori ‘reali’ rilevati per $k>7$. Completando la ricerca con maggiore ‘attenzione’ si è riusciti a ottenere una ‘soluzione’ con scarto quadratico medio inferiore. La soluzione è la seguente…
$eta=.513$
$p=6*10^(-3)$
$gamma=.5$ (6)
...con valore di m.s.e. pari a $5.5*10^(-3)$. La curva di distribuzione con i parametri (6) è mostrata il figura…

I valori di media e varianza sono i seguenti…
$mu=3.17$
$sigma^2=4.26$ (7)
I valori (7) sono assai più vicini ai valori ‘reali’ di quanto non lo siano i valori (5) per cui la soluzione (6) è certamente più ‘verosimile’ rispetto alla (4) e la cosa appare del tutto evidente osservando il grafico. Nell’ipotesi che la soluzione ora trovata sia quella ‘giusta’, calcoliamo quante debbono essere state le schede bianche 'desaparecidas’. Se le schede sono state in totale $1.793.446$, ad una valore $p=6*10^(-3)$ corrispondono $10.760$ ‘schede bianche’. Siccome le schede bianche ‘reali’ sono state in tutto $8.344$ le schede bianche 'desaparecidas sono $10.760-8.344=2.416$. In tal caso, dal momento che il risultato è stato deciso da una differenza di $24.000$ voti, $2416$ ‘schede manipolate’ nella sola Roma non rappresentano una entità ‘trascurabile’…
La soluzione ora descritta è stata ottenuta con criterio della ‘minimizzazione dello scarto quadratico’. Un altro criterio ‘accettabile’ è quello di cercare di minimizzare lo scarto nei valori di $mu$ e $sigma^2$. La ricerca eseguita con questo criterio ha fornito la soluzione seguente…
$eta=.4644$
$p=6.5*10^(-3)$
$gamma=. 46$ (8)
… con valore m.s.e. pari a $6.7*10^(-3)$. La curva di distribuzione con i parametri (8) è mostrata in figura…

I valori di media e varianza sono i seguenti…
$mu=3.24$
$sigma^2=4.71$ (9)
Nell’ipotesi che questa sia la soluzione ‘giusta’ la stima delle schede bianche 'desaparecidas', eseguita con metodo usato prima, fornisce un valore pari a $3.313$, maggiore dunque rispetto al valore trovato in precedenza e per questo ancora meno ‘trascurabile’ nel determinare il risultato del voto nazionale…
Questi i risultati dell’analisi. In attesa dei ‘commenti’ vostri [che sinceramente sono curioso di sentire

 …] sono lieto di porgere a tutti i miei più…
…] sono lieto di porgere a tutti i miei più… cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Lupo grigio la forza dei numeri può essere come quella che ha portato lo scienziato nazista di cui non ricordo il nome a dimostrare che la razza "superiore" aveva un cranio più capiente per contenere"più cervello"....riuscì a dimostrarlo e con molti numeri finiti regolarmente nel cesso di qualcuno che sapeva contare meglio di lui.
Ho notato per esempio una certa tendenza a rendere la curva approssimabile tracciandoci su una normale o una binomiale o quel che gli pare ma questa curva è una normale o una binomiale?
NO....quindi già la partenza è falsata...
In un controllo di qualità di laboratorio avrebberò già messo in quarantena i contatori e Roma non batte ciglio dopo tutto quello che è comparso.
Mi sembra che la partenza sia sbagliata perchè se guardi i grafici presenti su Politicaonline troverai che le stranezza si sommano alle stranezze e si presuppone non solo per piccole quantità di emergenza.
Esempio su un piccolissimo tratto di curva ho calcolato la possibilità di una mancanza per difetto di -800 schede bianche che difficilmente può essere spiegabile.
I calcoli a mio parere sono validi e accettabilissimi quando i presupposti sono certi, comunque buona fortuna ,credo che ne avrai molto bisogno,io ho sentito un'esperta di scienze esatte che col calcolo del Casolino fa ammontare il danno a 2milioni 800mila schede .......ribuona fortuna!!!!!
Ho notato per esempio una certa tendenza a rendere la curva approssimabile tracciandoci su una normale o una binomiale o quel che gli pare ma questa curva è una normale o una binomiale?
NO....quindi già la partenza è falsata...
In un controllo di qualità di laboratorio avrebberò già messo in quarantena i contatori e Roma non batte ciglio dopo tutto quello che è comparso.
Mi sembra che la partenza sia sbagliata perchè se guardi i grafici presenti su Politicaonline troverai che le stranezza si sommano alle stranezze e si presuppone non solo per piccole quantità di emergenza.
Esempio su un piccolissimo tratto di curva ho calcolato la possibilità di una mancanza per difetto di -800 schede bianche che difficilmente può essere spiegabile.
I calcoli a mio parere sono validi e accettabilissimi quando i presupposti sono certi, comunque buona fortuna ,credo che ne avrai molto bisogno,io ho sentito un'esperta di scienze esatte che col calcolo del Casolino fa ammontare il danno a 2milioni 800mila schede .......ribuona fortuna!!!!!
Cara Marisa
comprendo benissimo il tuo desiderio di 'validare' una certa 'teoria' in cui credi profondamente ma ti devo ricordare che siamo su un forum di Matematica e qui l'unica 'imparzialità' valida è la 'imparzialità' della legge dei numeri. Questa talvolta può essere 'dura' da accettare ma, come si diceva nell'antica Roma, dura lex sed lex...
Quanto al problema della 'distribuzione statistica' occorre precisare un concetto importante. La curva di distribuzione di un evento con probabilità $p$ osservato in $n$ esperimenti 'assomiglia' ad una distribuzione normale solo quando è verificata la condizione $n*p$>>$1$, ossia quando il numero di volte in cui si è verificato è, diciamo così, espresso da un numero intero di almeno due cifre. Per capire il concetto facciamo un esempio estremo, vale a dire che in $2600$ sezioni con quasi due milioni di elettori vi sia stata in tutto una scheda bianca. In questo è $p=5*10^(-7)$ e con $n=700$ si ha che $n*p$<<$1$. La distribuzione delle schede bianche in tal caso avrenne una forma assai 'strana' in quanto vi sarebbero $0$ schede in $2599$ sezioni, $1$ scheda in $1$ sezione e in nessuna sezione più $1$ scheda... una distribuzione che tutto può essere fuori che una 'normale'...
Per quanto riguarda l'analisi eseguita sulle schede bianche della circoscrizione di Roma ho detto subito che il risultato da me fornito non doveva considerarsi 'definitivo' in quanto restavano delle 'incoerenze', soprattutto per i valori di $k>7$. In effetti posso anticipare che con un esame più attento ho ottenuto risultati più 'corenti' che tra pochissimo saranno resi noti...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
comprendo benissimo il tuo desiderio di 'validare' una certa 'teoria' in cui credi profondamente ma ti devo ricordare che siamo su un forum di Matematica e qui l'unica 'imparzialità' valida è la 'imparzialità' della legge dei numeri. Questa talvolta può essere 'dura' da accettare ma, come si diceva nell'antica Roma, dura lex sed lex...
Quanto al problema della 'distribuzione statistica' occorre precisare un concetto importante. La curva di distribuzione di un evento con probabilità $p$ osservato in $n$ esperimenti 'assomiglia' ad una distribuzione normale solo quando è verificata la condizione $n*p$>>$1$, ossia quando il numero di volte in cui si è verificato è, diciamo così, espresso da un numero intero di almeno due cifre. Per capire il concetto facciamo un esempio estremo, vale a dire che in $2600$ sezioni con quasi due milioni di elettori vi sia stata in tutto una scheda bianca. In questo è $p=5*10^(-7)$ e con $n=700$ si ha che $n*p$<<$1$. La distribuzione delle schede bianche in tal caso avrenne una forma assai 'strana' in quanto vi sarebbero $0$ schede in $2599$ sezioni, $1$ scheda in $1$ sezione e in nessuna sezione più $1$ scheda... una distribuzione che tutto può essere fuori che una 'normale'...
Per quanto riguarda l'analisi eseguita sulle schede bianche della circoscrizione di Roma ho detto subito che il risultato da me fornito non doveva considerarsi 'definitivo' in quanto restavano delle 'incoerenze', soprattutto per i valori di $k>7$. In effetti posso anticipare che con un esame più attento ho ottenuto risultati più 'corenti' che tra pochissimo saranno resi noti...
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Lupo grigio,credo che quelle di cui parli siano tue speranze e che la realtà sia molto diversa,veramente non posso scendere nei particolari ma quello che ci si aspetta da un tale numero di sezioni (2600) è senz'altro una curva normale che non è quella che si ottiene mettendo in grafico i dati, soprattutto perchè riducendosi il numero delle schede una curva normale non può perdere "la testa" ma rimanere una normalissima normale con l'estremità a sinistra (sezioni con 0 schede bianche)con probabilità prossima allo zero(quasi aderente all'asse delle x),questa "testa tronca" inisieme alla scarsa variabilità intorno al valor medio e la spinta esagerata delle sezioni verso l'asse delle y (detto semplicemente)indicano che il grafico è stato manipolato e non per poche schede, .....sei sicuro di essere imparziale?
Il grafico esagerato che si è ottenuto testimonia che non c'è stato un semplice appiattimento delle schede bianche ma un intervento diciamo "imprudente".
La forma del grafico serve solo a capire che manca la garanzia anche solo di una regolarità apparente,da altri grafici si può capire meglio l'origine della manipolazione.
Il grafico esagerato che si è ottenuto testimonia che non c'è stato un semplice appiattimento delle schede bianche ma un intervento diciamo "imprudente".
La forma del grafico serve solo a capire che manca la garanzia anche solo di una regolarità apparente,da altri grafici si può capire meglio l'origine della manipolazione.
Ragazzi
sperando vi siate ben ‘sfogati’ dando ****tti a destra e a… no… anzi… a destra soltanto … , torniamo ad argomenti dal sapore più squisitamente matematico. A chi di voi segue il forum di matematica discreta [del quale il vecchio lupo è stato un po’ il ‘patrocinatore’…] non sarà certamente sfuggito il thread seguente…
… , torniamo ad argomenti dal sapore più squisitamente matematico. A chi di voi segue il forum di matematica discreta [del quale il vecchio lupo è stato un po’ il ‘patrocinatore’…] non sarà certamente sfuggito il thread seguente…
https://www.matematicamente.it/f/viewtopic.php?t=20400
Lì si parla diffusamente delle ‘malefatte’ dei postini di Manolestlanka, molti dei quali hanno la lodevole abitudine, nel caso si accorgano che una delle lettere che devono consegnare contiene denaro, di farla ‘sparire’ insieme al suo contenuto. Per esaminare il fenomeno dal punto di vista statistico si è dapprima ipotizzato di conoscere la probabilità $p$ che una lettera da recapitare contenga del denaro e la probabilità $gamma$ che il postino non se ne accorga ed essa giunga ‘integra’ al legittimo destinatario. Si è ipotizzato in un primo tempo che tutti i postini siano ‘disonesti’. In tal caso se $n$ è il numero di lettere assegnate a ciascun postino la probabilità che di queste $k$ contengano denaro e siano recapitate ‘integre’ è data da…
$P_(n,k)= ((n),(k))* (gamma*p)^k*(1-gamma*p)^(n-k)$ (1)
La (1) altro non è che la classica distribuzione binomiale in cui è…
$E[k]=mu=gamma*p*n$
$E[(k-mu)^2]=sigma^2= gamma*p*n*(1-gamma*p)$ (2)
Ora è evidente che nel caso in cui tutti i postini sono disonesti è possibile conoscere il prodotto $gamma*p$ ma è impossibile arrivare a conoscere $p$ e $gamma$ separatamente, vale a dire se vi è stato furto oppure no. In altre parole se i postini agiscono statisticamente tutti allo stesso modo possono star sicuri di ‘farla franca’, in quanto non è possibile dimostrare che vi è stato furto di denaro dalle lettere. La situazione cambia in modo drastico tuttavia se si fa l’ipotesi che non tutti i postini sono ‘disonesti’. Ipotizziamo che $eta$ sia la percentuale di postini ‘onesti’ e $1-eta$ la percentuale di postini ‘disonesti’ e che questi ultimi operino nel modo descritto prima. In tal caso la distribuzione diviene…
$p_(n,k)= ((n),(k))* [eta*p^k*(1-p)^(n-k)+(1-eta)*(gamma*p)^k*(1-gamma*p)^(n-k)$ (3)
Cacolando media e varianza si trova…
$E[k]=mu= n*p[eta+(1-eta)*gamma]$
$E[(k-mu]^2]=sigma^2= n^2*p^2*eta*(1-eta)*(1-gamma)^2+n*[eta*p*(1-p)+(1-eta)*gamma*p*(1-gamma*p)]$ (4)
L’ultima relazione trovata è della massima importanza. Se osserviamo con attenzione la formula della varianza notiamo la presenza del termine $n^2*p^2*eta*(1-eta)*(1-gamma)^2$ che si annulla per $eta=0$ [tutti i postini ‘disonesti’…] o per $eta=1$ [tutti i postini ‘onesti’…] ma che è non nullo negli altri casi e causa, a parità di ‘valor medio’ della $k$, un valore della varianza sensibilmente superiore rispetto al caso prima esaminato. Per avere un esempio indicativo osservate il seguente diagramma.

Si ipotizzato che ciascun postino debba recapitare $n=1000$ lettere e di queste in media $30$ contengono denaro, ossia $p=3*10^(-2)$. La curva rossa rappresenta il caso in cui tutti i postini sono 'disonesti' e di tre buste contenenti denaro ne facciano sparire una, ossia $gamma=2/3$. Con le formule (2) si trova che il valore medio delle buste arrivate ‘integre’ è $mu=20$ e la varianza $sigma^2=19.6$. La curva in nero invece rappresenta il caso in cui la metà dei postini è ‘onesta’ e l’altra metà ‘disonesta’ per cui è $eta=1/2$. Ipotizziamo in questo caso che i postini ‘disonesti’ facciamo sparire due buste contenenti denaro su tre, quindi $gamma=1/3$, e che sia sempre $p=3*10^(-2)$. Con le (4) si trova che il valor medio delle buste arrivate ‘integre’ è $mu=20$ [lo stesso di prima…], mentre la varianza è $sigma^2=119.5$ [una bella differenza rispetto a prima, non è vero?…]. Così in questo caso non solo siamo in grado di stabilire che il furto c’è stato, ma anche di calcolarne l’entità… niente male vero?…
Very good boys!… Ora vi propongo un simpatico giochino. Immaginiamo di cambiare scenario spostandoci a Roma durante le elezioni politiche dello scorso anno. Al posto dei postini di Manolestlanka vi sono le sezioni elettorali della circoscrizione di Roma e al posto delle ‘buste con denaro’ vi siano delle ‘schede bianche’. Vogliamo provare indovinare se in qualcuna di queste sezioni qualcuno ha fatto sparire delle ‘schede bianche’ e magari anche a calcolare quante ne sono sparite. Sappiamo che ciascuna sezione elettorale ha scrutinato $n=700$ e che le sezioni erano $2600$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 199
1 / 396
2 / 487
3 / 521
4 / 380
5 / 250
6 / 161
7 / 92
8 / 54
9 / 31
10 / 14
11 / 10
12 / 0
13 / 3
14 / 1
15 / 0
16 / 0
17 / 1
Gli stessi dati sono rappresentati dall’istogramma in nero nella figura seguente…

Se calcoliamo media e varianza otteniamo $mu=3.209$ e $sigma^2= 4.79$. Nel caso ‘teorico’ rappresentato dalla curva in rosso [ossia nel caso che la distribuzione obbedisse alla (1) e non ci siano stati ‘furti’ …] dovrebbe essere però $sigma^2=3.201$, ossia un valore notevolmente inferiore a quello ‘reale’. Questo ci autorizza quindi a ritenere possibile che in qualche sezione qualche ‘bravo ragazzo’ abbia trasformato qualche ‘scheda bianca’ in voti validi. Ora è ragionevole supporre che non in tutte le sezioni si sia potuto fare questo, magari a causa della presenza di rappresentati di lista dello schieramento avverso. Sarà dunque $eta$ [incognita…] la percentuale delle ‘sezioni oneste’ di Roma. Anche dove il ‘bravo ragazzo’ ha potuto agire si deve supporre che non abbia potuto agire su tutte le schede e chiamiamo $gamma$ [incognita…] la percentuale di schede bianche ‘sopravvissute’ nelle sezioni ‘disoneste’. Supponiamo sia $p$ infine la percentuale [incognita anch’essa…] di schede bianche ‘reali’, vale a dire le bianche deposte nell’urna nel corso delle votazioni. Come si fa a stimare le tre incognite $p$, $eta$ e $gamma$?... Il metodo ‘standard’ in questi casi è cercare i valori delle tre variabili che minimizzano lo scarto quadratico tra i valori rilevati e i valori calcolati con la (3). La ricerca è stata fatta ed ha fornito i risultati seguenti…
$eta=.8811$
$p=4.75*10^(-3)$
$gamma=.225$
La curva di distribuzione corrispondente è disegnata in rosso nel diagramma seguente…

Se calcoliamo i corrispondenti valori di $mu$ e $sigma^2$ con $n=700$ otteniamo $mu=3.01$ e $sigma^2=3.7$. Il valor medio è leggermente inferiore al valor medio ‘reale’. In compenso la varianza è assai più vicina alla varianza ‘reale’, per cui possiamo dire che il ‘modello’ ora proposto è assai più aderente alla realtà che non quello relativo ad una situazione ‘normale’. Da notare il numero relativamente alto di $eta$ [le sezioni ‘oneste’ sono $88$ su $100$…] e il valore relativamente basso di $gamma$ [nel $12$ per cento di sezioni ‘disoneste’ le schede bianche sono state ‘annientate’ e solo una su cinque è scampata…]. Pur essendo con ogni probabilità assai vicino alla realtà, il modello non è del tutto adeguato in quanto non giustifica il numero relativamente ‘alto’ di sezioni in cui si sono avute più di sette schede bianche. Ciò significa che il quadro reale deve essere stato ancora più ‘anomalo’ del quadro ora rappresentato e quanto prima si faranno ulteriori ‘accertamenti’ per appurare la ‘realtà’. Rimanendo però alla situazione illustrata dall’ultimo diagramma che cosa possiamo dire riguardo alle schede bianche ‘desaparecidas’?… Essendo il numero totale di schede scrutinate pari a $1.793.446$, un valore di $p=4.75*10^(-3)$ corrisponde ad $8.519$ ‘schede bianche’. Essendo state le schede bianche in realtà $8.344$, se ne deduce che le schede ‘desaparecidas’ sarebbero $8.519-8.344=175$. Ovvio che non sono ‘tantissime’ e se le cose stessero così è difficile sostenere che il ‘fenomeno’ abbia potuto incidere sul risultato. Come già detto però il ‘modello’ si avvicina solo in parte alla ‘realtà’ e qualche ulteriore ‘affinamento’ deve essere fatto. Per cui ragazzi… non perdete le prossime puntate!…
cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
sperando vi siate ben ‘sfogati’ dando ****tti a destra e a… no… anzi… a destra soltanto
 … , torniamo ad argomenti dal sapore più squisitamente matematico. A chi di voi segue il forum di matematica discreta [del quale il vecchio lupo è stato un po’ il ‘patrocinatore’…] non sarà certamente sfuggito il thread seguente…
… , torniamo ad argomenti dal sapore più squisitamente matematico. A chi di voi segue il forum di matematica discreta [del quale il vecchio lupo è stato un po’ il ‘patrocinatore’…] non sarà certamente sfuggito il thread seguente… https://www.matematicamente.it/f/viewtopic.php?t=20400
Lì si parla diffusamente delle ‘malefatte’ dei postini di Manolestlanka, molti dei quali hanno la lodevole abitudine, nel caso si accorgano che una delle lettere che devono consegnare contiene denaro, di farla ‘sparire’ insieme al suo contenuto. Per esaminare il fenomeno dal punto di vista statistico si è dapprima ipotizzato di conoscere la probabilità $p$ che una lettera da recapitare contenga del denaro e la probabilità $gamma$ che il postino non se ne accorga ed essa giunga ‘integra’ al legittimo destinatario. Si è ipotizzato in un primo tempo che tutti i postini siano ‘disonesti’. In tal caso se $n$ è il numero di lettere assegnate a ciascun postino la probabilità che di queste $k$ contengano denaro e siano recapitate ‘integre’ è data da…
$P_(n,k)= ((n),(k))* (gamma*p)^k*(1-gamma*p)^(n-k)$ (1)
La (1) altro non è che la classica distribuzione binomiale in cui è…
$E[k]=mu=gamma*p*n$
$E[(k-mu)^2]=sigma^2= gamma*p*n*(1-gamma*p)$ (2)
Ora è evidente che nel caso in cui tutti i postini sono disonesti è possibile conoscere il prodotto $gamma*p$ ma è impossibile arrivare a conoscere $p$ e $gamma$ separatamente, vale a dire se vi è stato furto oppure no. In altre parole se i postini agiscono statisticamente tutti allo stesso modo possono star sicuri di ‘farla franca’, in quanto non è possibile dimostrare che vi è stato furto di denaro dalle lettere. La situazione cambia in modo drastico tuttavia se si fa l’ipotesi che non tutti i postini sono ‘disonesti’. Ipotizziamo che $eta$ sia la percentuale di postini ‘onesti’ e $1-eta$ la percentuale di postini ‘disonesti’ e che questi ultimi operino nel modo descritto prima. In tal caso la distribuzione diviene…
$p_(n,k)= ((n),(k))* [eta*p^k*(1-p)^(n-k)+(1-eta)*(gamma*p)^k*(1-gamma*p)^(n-k)$ (3)
Cacolando media e varianza si trova…
$E[k]=mu= n*p[eta+(1-eta)*gamma]$
$E[(k-mu]^2]=sigma^2= n^2*p^2*eta*(1-eta)*(1-gamma)^2+n*[eta*p*(1-p)+(1-eta)*gamma*p*(1-gamma*p)]$ (4)
L’ultima relazione trovata è della massima importanza. Se osserviamo con attenzione la formula della varianza notiamo la presenza del termine $n^2*p^2*eta*(1-eta)*(1-gamma)^2$ che si annulla per $eta=0$ [tutti i postini ‘disonesti’…] o per $eta=1$ [tutti i postini ‘onesti’…] ma che è non nullo negli altri casi e causa, a parità di ‘valor medio’ della $k$, un valore della varianza sensibilmente superiore rispetto al caso prima esaminato. Per avere un esempio indicativo osservate il seguente diagramma.

Si ipotizzato che ciascun postino debba recapitare $n=1000$ lettere e di queste in media $30$ contengono denaro, ossia $p=3*10^(-2)$. La curva rossa rappresenta il caso in cui tutti i postini sono 'disonesti' e di tre buste contenenti denaro ne facciano sparire una, ossia $gamma=2/3$. Con le formule (2) si trova che il valore medio delle buste arrivate ‘integre’ è $mu=20$ e la varianza $sigma^2=19.6$. La curva in nero invece rappresenta il caso in cui la metà dei postini è ‘onesta’ e l’altra metà ‘disonesta’ per cui è $eta=1/2$. Ipotizziamo in questo caso che i postini ‘disonesti’ facciamo sparire due buste contenenti denaro su tre, quindi $gamma=1/3$, e che sia sempre $p=3*10^(-2)$. Con le (4) si trova che il valor medio delle buste arrivate ‘integre’ è $mu=20$ [lo stesso di prima…], mentre la varianza è $sigma^2=119.5$ [una bella differenza rispetto a prima, non è vero?…]. Così in questo caso non solo siamo in grado di stabilire che il furto c’è stato, ma anche di calcolarne l’entità… niente male vero?…
Very good boys!… Ora vi propongo un simpatico giochino. Immaginiamo di cambiare scenario spostandoci a Roma durante le elezioni politiche dello scorso anno. Al posto dei postini di Manolestlanka vi sono le sezioni elettorali della circoscrizione di Roma e al posto delle ‘buste con denaro’ vi siano delle ‘schede bianche’. Vogliamo provare indovinare se in qualcuna di queste sezioni qualcuno ha fatto sparire delle ‘schede bianche’ e magari anche a calcolare quante ne sono sparite. Sappiamo che ciascuna sezione elettorale ha scrutinato $n=700$ e che le sezioni erano $2600$. La tabella schede bianche/numero di sezioni è la seguente…
schede bianche/numero sezioni
0 / 199
1 / 396
2 / 487
3 / 521
4 / 380
5 / 250
6 / 161
7 / 92
8 / 54
9 / 31
10 / 14
11 / 10
12 / 0
13 / 3
14 / 1
15 / 0
16 / 0
17 / 1
Gli stessi dati sono rappresentati dall’istogramma in nero nella figura seguente…

Se calcoliamo media e varianza otteniamo $mu=3.209$ e $sigma^2= 4.79$. Nel caso ‘teorico’ rappresentato dalla curva in rosso [ossia nel caso che la distribuzione obbedisse alla (1) e non ci siano stati ‘furti’ …] dovrebbe essere però $sigma^2=3.201$, ossia un valore notevolmente inferiore a quello ‘reale’. Questo ci autorizza quindi a ritenere possibile che in qualche sezione qualche ‘bravo ragazzo’ abbia trasformato qualche ‘scheda bianca’ in voti validi. Ora è ragionevole supporre che non in tutte le sezioni si sia potuto fare questo, magari a causa della presenza di rappresentati di lista dello schieramento avverso. Sarà dunque $eta$ [incognita…] la percentuale delle ‘sezioni oneste’ di Roma. Anche dove il ‘bravo ragazzo’ ha potuto agire si deve supporre che non abbia potuto agire su tutte le schede e chiamiamo $gamma$ [incognita…] la percentuale di schede bianche ‘sopravvissute’ nelle sezioni ‘disoneste’. Supponiamo sia $p$ infine la percentuale [incognita anch’essa…] di schede bianche ‘reali’, vale a dire le bianche deposte nell’urna nel corso delle votazioni. Come si fa a stimare le tre incognite $p$, $eta$ e $gamma$?... Il metodo ‘standard’ in questi casi è cercare i valori delle tre variabili che minimizzano lo scarto quadratico tra i valori rilevati e i valori calcolati con la (3). La ricerca è stata fatta ed ha fornito i risultati seguenti…
$eta=.8811$
$p=4.75*10^(-3)$
$gamma=.225$
La curva di distribuzione corrispondente è disegnata in rosso nel diagramma seguente…

Se calcoliamo i corrispondenti valori di $mu$ e $sigma^2$ con $n=700$ otteniamo $mu=3.01$ e $sigma^2=3.7$. Il valor medio è leggermente inferiore al valor medio ‘reale’. In compenso la varianza è assai più vicina alla varianza ‘reale’, per cui possiamo dire che il ‘modello’ ora proposto è assai più aderente alla realtà che non quello relativo ad una situazione ‘normale’. Da notare il numero relativamente alto di $eta$ [le sezioni ‘oneste’ sono $88$ su $100$…] e il valore relativamente basso di $gamma$ [nel $12$ per cento di sezioni ‘disoneste’ le schede bianche sono state ‘annientate’ e solo una su cinque è scampata…]. Pur essendo con ogni probabilità assai vicino alla realtà, il modello non è del tutto adeguato in quanto non giustifica il numero relativamente ‘alto’ di sezioni in cui si sono avute più di sette schede bianche. Ciò significa che il quadro reale deve essere stato ancora più ‘anomalo’ del quadro ora rappresentato e quanto prima si faranno ulteriori ‘accertamenti’ per appurare la ‘realtà’. Rimanendo però alla situazione illustrata dall’ultimo diagramma che cosa possiamo dire riguardo alle schede bianche ‘desaparecidas’?… Essendo il numero totale di schede scrutinate pari a $1.793.446$, un valore di $p=4.75*10^(-3)$ corrisponde ad $8.519$ ‘schede bianche’. Essendo state le schede bianche in realtà $8.344$, se ne deduce che le schede ‘desaparecidas’ sarebbero $8.519-8.344=175$. Ovvio che non sono ‘tantissime’ e se le cose stessero così è difficile sostenere che il ‘fenomeno’ abbia potuto incidere sul risultato. Come già detto però il ‘modello’ si avvicina solo in parte alla ‘realtà’ e qualche ulteriore ‘affinamento’ deve essere fatto. Per cui ragazzi… non perdete le prossime puntate!…

cordiali saluti
lupo grigio

An old wolf may lose his teeth, but never his nature
Ma per favore, non diciamo sciocchezze.
Con l'età media dell'elettorato italiano vi pare che in 5 anni vi possa essere uno sconvolgimento comportamentale del genere?
Quando vado in laboratorio posso scambiare un risonanza magnetica con un contatto sbagliato; ma quei dati sono una dimostrazione statistica che i voti sono stati manipolati.
Quando hai la glicemia a 300 non è mica una prova che hai il diabete, però magari ci guardi dentro, no?
Con l'età media dell'elettorato italiano vi pare che in 5 anni vi possa essere uno sconvolgimento comportamentale del genere?
Quando vado in laboratorio posso scambiare un risonanza magnetica con un contatto sbagliato; ma quei dati sono una dimostrazione statistica che i voti sono stati manipolati.
Quando hai la glicemia a 300 non è mica una prova che hai il diabete, però magari ci guardi dentro, no?
"Cheguevilla":
@ wedge: Il grafico che riporti è molto interessante e mostra in maniera piuttosto diretta l'evidenza. Mi permetto di aggiungere alcuni particolari "esogeni":
- Si può notare un forte innalzamento successivamente al 1992. Questo fu interpretato dai "tecnici" come una cosa dovuta essenzialmente a due cause: la legge elettorale (276 e 277 del 1993) con il passaggio al sistema uninominale ed il clima di sfiducia nella politica successivo al caso "Tangentopoli".
Per quanto riguarda la nuova legge elettorale, essendo ancora più rigida nella scelta, trovo impossibile che questa abbia condotto ad un calo delle schede bianche.
Il clima di fiducia verso la politica non è certamente cambiato in meglio.
Ma magari il terrore di altri 5 anni di berlusconismo ha mobilitato forze che normalmente si astengono per la sfiducia di cui si parlava prima....
"tecnos":
Quando si parla di politica si finisce sempre ai soliti punti...
Esatto. Per questo sono sempre dell'idea che certi discorsi andrebbero vietati, onde preservare la quiete e l'armonia del forum.
"jpe535887":
[quote="GIOVANNI IL CHIMICO"]Sì, una democrazia. Guidata quanto vuoi e menomata quanto ti pare ma pur sempre una democrazia, tanto è vero che si sono tenute libere elezioni.
anche oggi siamo in una dittatura amico mio. un tempo i dissidenti si facevano una bella bevuta di olio di ricino, oggi vengono soffocati dalle verità omologate delle tv e dei giornali servitori del potere ( se uno dice A e 100000000 dicono B cosa risalta?), vengono intimiditi con querele e oscuramenti di blog (mai sentito parlare di piero ricca? vai sul sito di beppe grillo e scorrendo con la barra potrai tuffarti in una breve ma istruttiva lettura... se hai tempo vai anche su youtube e cerca piero ricca+fede e piero ricca+sgarbi...). noi siamo pecore che pensano di stare bene perchè hanno un cellulare che fa foto, filmati e tante belle lucette! siamo tramortiti da 8-10-12 ore di lavoro al giorno (non tutte pagate) che ci succhiano la linfa vitale lasciandoci solo l'energia necessaria per accendere la tv sul divano per sentire le loro cazzate o assistere all'indegno risultato del canone rai che tu hai pagato. chi non ha il lavoro invece lo cerca, viene assunto con un contratto a tempo determinato senza la data della scadenza segnata, quando rompe i coglioni viene licenziato perchè magicamente il suo contratto finiva quel giorno e tutto ricomincia da capo! andiamo a votare e non possiamo neanche scegliere il nostro candidato. i criminali occupano le istituzioni e vanno in pensione dopo 35 mesi di poltronaggio (dopo aver percepito 15000 euro mensili) e a noi alzeranno l'età pensionabile.
nonostante ciò ci sono ancora tanti coglioni che si identificano in uno o nell'altro schieramento e criticano quello avverso quando governa, mettendosi il paraocchi, e tutta l'intelligenza che mostrano risolvendo un problema matematco svanisce davanti ad un'argomento socio-politico. se volete bannarmi per questo insulto fate pure...
saluti a tutti[/quote] ci hai preso!

"jpe535887":
nonostante ciò ci sono ancora tanti coglioni che si identificano in uno o nell'altro schieramento e criticano quello avverso quando governa, mettendosi il paraocchi...
Sono daccordo con te al 100%!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo