Probabilità eventi non accadano r volte consecutive
Prendiamo come riferimento il lancio di un dado (che ci semplifica il tutto).
Abbiamo per ogni numero:
$p=1/6$
$q=1-1/6=5/6$
$m=1/(1/6)=6 $(è il numero di tutti i possibili eventi elementari equiprobabili)
Ora sappiamo che ogni singolo numero ha probabilità $q^n$ di non uscire $n$ volte consecutive
ad ogni lancio il "6" (lo prendo come esempio) ha sempre $1/6$ di probabilità di uscire. Ovviamente non dipende dal ritardo che il numero ha in quel momento, al contrario di quanti pensano che convenga giocare al lotto numeri ritardatari. Posso dire che esce in media ogni 6 estrazioni.
Ora un passo difficile: quello che voglio io, è trovare una formula che mi dia la probabilità di ritardo $r$ su $m$ numeri complessivi.
Per intenderci, se considerassi un solo numero, il ritardo su $r$ estrazioni (ovviamente considero $r $ come totale di estrazioni) sarebbe chiaramente $q^r$.
Ma se considero tutti i sei numeri di un dado, la formula non è corretta, perchè la probabilità è ovviamente piú bassa...infatti guarda questo esempio:
Escono 1,2,3,4,6,3
Quindi con $r=6$ ho 6 come massimo ritardo complessivo, ma esso non è dato dal numero "6".
Per calcolare la probabilità complessiva, userei doppiamente la complementare:
Considera $r$ (credo che per evitare problemi,convenga sempre porre $r>6$) lanci consecutivi: la probabilità che un singolo numero non esca mai è data da $(5/6)^r$, da cui la probabilitá che un singolo numero esca almeno una volta è data da $1-(5/6)^r$.
Ora possiamo calcolare la probabilitá che tutti i numeri escano almeno una volta sarebbe* data da $(1-(5/6)^r)^6$ e la probabilità che almeno uno di essi ritardi $P=1-(1-(5/6)^r)^6)$
*chiaramente c'è un errore, perchè non considero che gli eventi non sono completamente indipendenti.
Avendo trovato $P$, credo che si potrebbe pensare al problema nella sua completezza... Qualcuno saprebbe correggermi la formula per Trovare $P$?
non so se sono stato chiaro... In poche (altre?) parole:
Tiro $r$ volte un dado: la probabilità che non esca mai il "sei" è data da $(5/6)^r$, ma qual è la probabilità che nei $r$ lanci non compaia mai uno qualunque dei numeri?
Abbiamo per ogni numero:
$p=1/6$
$q=1-1/6=5/6$
$m=1/(1/6)=6 $(è il numero di tutti i possibili eventi elementari equiprobabili)
Ora sappiamo che ogni singolo numero ha probabilità $q^n$ di non uscire $n$ volte consecutive
ad ogni lancio il "6" (lo prendo come esempio) ha sempre $1/6$ di probabilità di uscire. Ovviamente non dipende dal ritardo che il numero ha in quel momento, al contrario di quanti pensano che convenga giocare al lotto numeri ritardatari. Posso dire che esce in media ogni 6 estrazioni.
Ora un passo difficile: quello che voglio io, è trovare una formula che mi dia la probabilità di ritardo $r$ su $m$ numeri complessivi.
Per intenderci, se considerassi un solo numero, il ritardo su $r$ estrazioni (ovviamente considero $r $ come totale di estrazioni) sarebbe chiaramente $q^r$.
Ma se considero tutti i sei numeri di un dado, la formula non è corretta, perchè la probabilità è ovviamente piú bassa...infatti guarda questo esempio:
Escono 1,2,3,4,6,3
Quindi con $r=6$ ho 6 come massimo ritardo complessivo, ma esso non è dato dal numero "6".
Per calcolare la probabilità complessiva, userei doppiamente la complementare:
Considera $r$ (credo che per evitare problemi,convenga sempre porre $r>6$) lanci consecutivi: la probabilità che un singolo numero non esca mai è data da $(5/6)^r$, da cui la probabilitá che un singolo numero esca almeno una volta è data da $1-(5/6)^r$.
Ora possiamo calcolare la probabilitá che tutti i numeri escano almeno una volta sarebbe* data da $(1-(5/6)^r)^6$ e la probabilità che almeno uno di essi ritardi $P=1-(1-(5/6)^r)^6)$
*chiaramente c'è un errore, perchè non considero che gli eventi non sono completamente indipendenti.
Avendo trovato $P$, credo che si potrebbe pensare al problema nella sua completezza... Qualcuno saprebbe correggermi la formula per Trovare $P$?
non so se sono stato chiaro... In poche (altre?) parole:
Tiro $r$ volte un dado: la probabilità che non esca mai il "sei" è data da $(5/6)^r$, ma qual è la probabilità che nei $r$ lanci non compaia mai uno qualunque dei numeri?
Risposte
Puoi usare il principio di escusione/inclusione.
Se chiami $A_i = "il numero i esce almeno una volta"$, hai che
$P( bigcap_{i=1}^6 A_i ) = 1-P(bigcup_{i=1}^6 A_i^c)$
Se chiami $A_i = "il numero i esce almeno una volta"$, hai che
$P( bigcap_{i=1}^6 A_i ) = 1-P(bigcup_{i=1}^6 A_i^c)$
Quindi? Scusa non ho capito perfettamente...
Quindi
$P(bigcup_i A_i^c) = 6 P(A_1^c) - ((6),(2)) P(A_1^c cap A_2^c) + ...$
$P(bigcup_i A_i^c) = 6 P(A_1^c) - ((6),(2)) P(A_1^c cap A_2^c) + ...$
Saresti cosí gentile da farmi un esempio?
Lancio 7 volte un dado, qual è la probabilità che almeno un numero non si veda?
Lancio 7 volte un dado, qual è la probabilità che almeno un numero non si veda?
"kobeilprofeta":
Saresti cosí gentile da farmi un esempio?
Lancio 7 volte un dado, qual è la probabilità che almeno un numero non si veda?
p = 15.120 / 279.936 [Circa il 5,4%]
Calcolato come casi favorevoli su totali
I totali $6^n$
I favorevoli possono essere calcolati con la formuletta:
f(n) = $6^n$ - $C(6,5)*5^n$ + $C(6,4)*4^n$ - $C(6,3)*3^n$ + $C(6,2)*2^n$ - $C(6,1)$
per il tuo caso n=7, quindi
f(7) = 279.936 - 6*78125 + 15*16384 - 20*2187 + 15*128 - 6
Grazie.
Per vedere se ho capito:
Nel lotto (p=5/90=1/18) la probabilità che in 100 estrazioni (10 ruote) non esca un qualunque numero e data da:
$p=frac{18^1000-C(18,17)*17^1000+C(18,16)*16^1000-...+C(18,2)*2^1000-C(18,1)}{18^1000}$
?
Per vedere se ho capito:
Nel lotto (p=5/90=1/18) la probabilità che in 100 estrazioni (10 ruote) non esca un qualunque numero e data da:
$p=frac{18^1000-C(18,17)*17^1000+C(18,16)*16^1000-...+C(18,2)*2^1000-C(18,1)}{18^1000}$
?
"kobeilprofeta":
Grazie.
Per vedere se ho capito:
Simularla con excel, è un po più ardua, in quanto le formule più lunghe...
Nel caso precedente la tabella excel, mostra come cambia la p. aumentando il numero dei lanci.
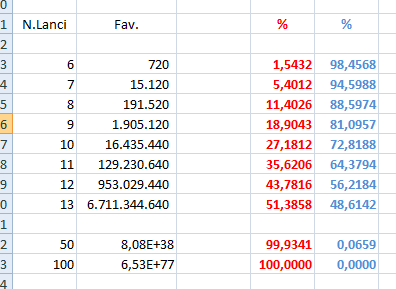
Con soli 6 lanci la p. che ci siano tutti i 6 numeri è bassissima (1,5%), con un settimo lancio si passa già al 5,4%. Ci vogliono ben 13 lanci per superare il 50%, al 50esimo siamo già quasi arrivati al 100%
Ma è giusta la formula che ho scritto sopra per il lotto? In pratica continuo a mettere un "+" se il numero è pari, un "-" se è dispari?
Mi sembra tutto ok... 
E' come se stai tirando 1000 dadi insieme, dove ogni dado ha 18 facce numerate da 1 a 18, e vuoi calcolare la p. che siano uscite tutti i 18 numeri. Sicuramente questa p. si avvicina al 100%.
La prima p. valida è quella con 18 dadi (la p. è quasi zero ... 0,00001627%) [Lanci 18 dadi a 18 facce, ed hai il cxxx che ci sono tutti i 18 numeri..)
Con 30 dadi si ha circa 1%
Con 50 dadi il 31%
Con 100 il 94%
Con 200 il 99,98%
Con 1000 excel, va in tilt.
Per verificare la bontà della tua formuletta, potresti simulare proprio i 18 lanci, e vedere se ti da come risultato la p. sopracitata, (0,00001627%...)
La stessa p. può essere calcolata con: $(17!) / (18^17)$
che nasce dal fatto che il primo dado può essere qualsiasi numero, il secondo 17 su 18, il terzo 16 su 18 ......

E' come se stai tirando 1000 dadi insieme, dove ogni dado ha 18 facce numerate da 1 a 18, e vuoi calcolare la p. che siano uscite tutti i 18 numeri. Sicuramente questa p. si avvicina al 100%.
La prima p. valida è quella con 18 dadi (la p. è quasi zero ... 0,00001627%) [Lanci 18 dadi a 18 facce, ed hai il cxxx che ci sono tutti i 18 numeri..)
Con 30 dadi si ha circa 1%
Con 50 dadi il 31%
Con 100 il 94%
Con 200 il 99,98%
Con 1000 excel, va in tilt.

Per verificare la bontà della tua formuletta, potresti simulare proprio i 18 lanci, e vedere se ti da come risultato la p. sopracitata, (0,00001627%...)
La stessa p. può essere calcolata con: $(17!) / (18^17)$
che nasce dal fatto che il primo dado può essere qualsiasi numero, il secondo 17 su 18, il terzo 16 su 18 ......
Grazie mille, molto gentile e chiaro. Scusa se insisto (lo farò ancora), ma mi interessa capire il "perchè"... Da dove esce quella formula? Qual è il ragionamento? La prima, non $frac{17!}{18^17}$.
Scusa se sono stato un po criptico, ma il mio scopo è sempre quello di farci arrivare alla soluzione.
L'impostazione co gli eventi che ti ho scritto me la ha inculcata il mio professore di probabilità. Infatti, usando le regole degli insiemi, si può quasi sempre pervenire ad una strutturazione più facile degli eventi.
In questo caso
$P(bigcup_{i=i}^6 A_i^c)=$
$=P(A_1^c)+...+P(A_6^c)+$
$-P(A_1^c cap A_2^c) - ...-P(A_5^c cap A_6^c)+$
$+ P(A_1^c cap A_2^c cap A_3^c)+ ...+P(A_4^c cap A_5^c cap A_6^c)-$
$...$
$-P(A_1^c cap A_2^c cap A_3^c cap A_4^c cap A_5^c cap A_6^c)$
Questa e' la legge delle probabilita' totali.
Ora, ogni probabilita di ogni riga di quella formula e' uguale (i numeri sono interscambiabili).
Dunque devi solo contare quante sono le scelte dei k eventi da 6: questi sono $((6),(k))$.
Dunque la probabilita' e':
$((6),(1)) P(A_1^c)+$
$-((6),(2)) P(A_1^c cap A_2^c)$
eccetra eccetra.
Ora devi calcolare le probabilita' delle intersezioni; ma queste sono facili perche' stai calcolando che su 7 lanci di un dado 1,2,3... facce non si presentano. Queste sono dunque $(5/6)^7, \quad (4/6)^7,...$.
Mattendo tutto insieme ottieni:
$((6),(1)) (5/6)^7 - ((6),(2)) (4/6)^7 + ((6),(3)) (3/6)^7 - ((6),(4)) (2/6)^7 + ((6),(5)) (1/6)^7 - ((6),(6)) (0/6)^7$.
questa e' uguale a 94.6% circa.
Nota che alla fine questa formula e' uguale a quella di Umby; i casi favorevoli si possono infatti ottenere con il principio di inclusione/esclusione.
L'impostazione co gli eventi che ti ho scritto me la ha inculcata il mio professore di probabilità. Infatti, usando le regole degli insiemi, si può quasi sempre pervenire ad una strutturazione più facile degli eventi.
In questo caso
$P(bigcup_{i=i}^6 A_i^c)=$
$=P(A_1^c)+...+P(A_6^c)+$
$-P(A_1^c cap A_2^c) - ...-P(A_5^c cap A_6^c)+$
$+ P(A_1^c cap A_2^c cap A_3^c)+ ...+P(A_4^c cap A_5^c cap A_6^c)-$
$...$
$-P(A_1^c cap A_2^c cap A_3^c cap A_4^c cap A_5^c cap A_6^c)$
Questa e' la legge delle probabilita' totali.
Ora, ogni probabilita di ogni riga di quella formula e' uguale (i numeri sono interscambiabili).
Dunque devi solo contare quante sono le scelte dei k eventi da 6: questi sono $((6),(k))$.
Dunque la probabilita' e':
$((6),(1)) P(A_1^c)+$
$-((6),(2)) P(A_1^c cap A_2^c)$
eccetra eccetra.
Ora devi calcolare le probabilita' delle intersezioni; ma queste sono facili perche' stai calcolando che su 7 lanci di un dado 1,2,3... facce non si presentano. Queste sono dunque $(5/6)^7, \quad (4/6)^7,...$.
Mattendo tutto insieme ottieni:
$((6),(1)) (5/6)^7 - ((6),(2)) (4/6)^7 + ((6),(3)) (3/6)^7 - ((6),(4)) (2/6)^7 + ((6),(5)) (1/6)^7 - ((6),(6)) (0/6)^7$.
questa e' uguale a 94.6% circa.
Nota che alla fine questa formula e' uguale a quella di Umby; i casi favorevoli si possono infatti ottenere con il principio di inclusione/esclusione.
Grazie della spiegazione, devo prendermi un po' di tempo per cercare di capirci qualcosa (non ho mai fatto nè prob, ne statistica).
Comunque che le formule siano equivalenti, lo si verifica dividendo la tua per $6^7$ e si ottiene $p=frac{favorevoli}{possibili}$, questo l'ho capito...
Comunque che le formule siano equivalenti, lo si verifica dividendo la tua per $6^7$ e si ottiene $p=frac{favorevoli}{possibili}$, questo l'ho capito...
Prego, spero solo di non aver fatto confusione.
Cerco di spiegarti la logica del principio di inclusione-esclusione.
Pensa ad un dado con 4 facce.
Vuoi contare le volte che un numero non si presenti.
Il numero 1 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 1
Il numero 2 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 2
Il numero 3 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 3
Il numero 4 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 4
Nel caso 1 hai delle setteplu del tipo $(2,3,3,4,3,2,3)$ oppure $(4,4,3,4,4,3,3)$.
In particolare la seconda 7-upla non contiene neanche il 2, ma allora appartiene anche al caso 2.
Se quindi sommi le possibilita' dei 4 casi $3^7 + 3^7 + 3^7 + 3^7$ conti alcune sequenze piu' di una volta.
In particolare le sequenze contate piu' di una volta sono quelle dove non compaiono tutti gli altri tre numeri, (solo un numero o due).
Piu precisamente sequenze con due numeri tipo $(4,4,3,4,4,3,3)$ compaiono due volte (caso 1 e caso 2);
quelle con un solo numero tipo $(1,1,1,1,1,1,1)$ compaiono tre volte (caso 2, caso 3, caso 4)
Quindi contiamole ed andiamo a toglierle.
Quante sono?
Be si potrebbe fare uno stesso ragionamento:
consideri tutte le coppie dei 4 numeri
(1,2) (1,3) (1,4)
(2,3) (2,4)
(3,4)
che sono $ 6 = ((4),(2))$
Per ogni coppia puoi considerare il numero di 7-uple che non contengono i numeri nella coppia: 2^7.
In questo conteggio le 7plue con due numeri diversi tipo $(4,4,3,4,4,3,3)$ compaiono una volta sola (questa nel caso (1,2)); quelle con un numero solo tipo $(1,1,1,1,1,1,1)$ compaiono tre volte.
Quindi sottraendo $4*3^7 - 6*2^7$
siamo apposto con le sequenze con tre numeri diversi (contate una volta nel primo addendo e non sottratte);
siamo apposto con le sequenze che contengono 2 numeri diversi (contate due volte nel primo addendo, ma tolte una volta sola nel secondo)
non siamo apposto per le (quattro) sequenze che contengo un solo numero.
Queste sono state contate 3 volte nel primo conteggio e tolte 3 volte nel secondo conteggio; bisogna dunque riaggiungerle. Quante sono? $4 * 1^7$.
In definitiva:
$((4),(1)) 3^7 - ((4),(2)) 2^7 + ((4),(1)) 1^7$
Vediamo se ora ci sono riuscito...a fare confusione
Cerco di spiegarti la logica del principio di inclusione-esclusione.
Pensa ad un dado con 4 facce.
Vuoi contare le volte che un numero non si presenti.
Il numero 1 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 1
Il numero 2 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 2
Il numero 3 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 3
Il numero 4 non si presenta nelle sequenze che usano gli altri tre numeri: $3^7$; caso 4
Nel caso 1 hai delle setteplu del tipo $(2,3,3,4,3,2,3)$ oppure $(4,4,3,4,4,3,3)$.
In particolare la seconda 7-upla non contiene neanche il 2, ma allora appartiene anche al caso 2.
Se quindi sommi le possibilita' dei 4 casi $3^7 + 3^7 + 3^7 + 3^7$ conti alcune sequenze piu' di una volta.
In particolare le sequenze contate piu' di una volta sono quelle dove non compaiono tutti gli altri tre numeri, (solo un numero o due).
Piu precisamente sequenze con due numeri tipo $(4,4,3,4,4,3,3)$ compaiono due volte (caso 1 e caso 2);
quelle con un solo numero tipo $(1,1,1,1,1,1,1)$ compaiono tre volte (caso 2, caso 3, caso 4)
Quindi contiamole ed andiamo a toglierle.
Quante sono?
Be si potrebbe fare uno stesso ragionamento:
consideri tutte le coppie dei 4 numeri
(1,2) (1,3) (1,4)
(2,3) (2,4)
(3,4)
che sono $ 6 = ((4),(2))$
Per ogni coppia puoi considerare il numero di 7-uple che non contengono i numeri nella coppia: 2^7.
In questo conteggio le 7plue con due numeri diversi tipo $(4,4,3,4,4,3,3)$ compaiono una volta sola (questa nel caso (1,2)); quelle con un numero solo tipo $(1,1,1,1,1,1,1)$ compaiono tre volte.
Quindi sottraendo $4*3^7 - 6*2^7$
siamo apposto con le sequenze con tre numeri diversi (contate una volta nel primo addendo e non sottratte);
siamo apposto con le sequenze che contengono 2 numeri diversi (contate due volte nel primo addendo, ma tolte una volta sola nel secondo)
non siamo apposto per le (quattro) sequenze che contengo un solo numero.
Queste sono state contate 3 volte nel primo conteggio e tolte 3 volte nel secondo conteggio; bisogna dunque riaggiungerle. Quante sono? $4 * 1^7$.
In definitiva:
$((4),(1)) 3^7 - ((4),(2)) 2^7 + ((4),(1)) 1^7$
Vediamo se ora ci sono riuscito...a fare confusione

Altro che confusione... Sei stato praticamente perfetto nella spiegazione... Grazie
Ps:
[ot]a breve (o a lungo) creerò un nuovo topic per chiedere/mostrare qualcosa che usa la formula che mi avete/hai dato/spiegato qua. Magari mi aiuterai/aiuterete ancora... Ciao[/ot]
Ps:
[ot]a breve (o a lungo) creerò un nuovo topic per chiedere/mostrare qualcosa che usa la formula che mi avete/hai dato/spiegato qua. Magari mi aiuterai/aiuterete ancora... Ciao[/ot]
"kobeilprofeta":
Per vedere se ho capito:
Nel lotto (p=5/90=1/18) la probabilità che in 100 estrazioni (10 ruote) non esca un qualunque numero e data da:
$p=frac{18^1000-C(18,17)*17^1000+C(18,16)*16^1000-...+C(18,2)*2^1000-C(18,1)}{18^1000}$
?
Per il lotto non è esattamente così.
E' vero che ad ogni estrazione escono 5 numeri su 90, quindi la probabilità è 1/18, ma per un calcolo preciso del numero di numeri che mano a mano vengono estratti devono essere considerati singolarmente i 90 numeri, non si può raggrupparli a 5 per volta.
Il calcolo è un po' laborioso, ma con le catene di Markov si può fare utilizzando un foglio excel.
Dopo la prima estrazione escono ovviamente 5 numeri con probabilità 1.
Alla seconda estrazione si possono verificare i seguenti 6 casi:
1) Ripetizione degli stessi 5 numeri p = 2,275E-08
2) Ripetizione di 4 numeri (presenza di 6 numeri) p = 9,670E-06
3) Ripetizione di 3 numeri (presenza di 7 numeri) p = 0,0008123
4) Ripetizione di 2 numeri (presenza di 8 numeri) p = 0,022474
5) Ripetizione di 1 numero (presenza di 9 numeri) p = 0,23035
6) Nessuna ripetizione (presenza di 10 numeri) p = 0,74635
Con le estrazioni successive, i casi possibili aumentano e i calcoli si complicano, ma con excel è "relativamente" semplice fare copia-incolla per completare la tabella fino, ad esempio, a 500 estrazioni.
A titolo di curiosità, 18 estrazioni sono ovviamente il numero minimo per avere l'uscita di tutti i 90 numeri (la probabilità è 1,4912E-37), mentre la probabilità più alta si ha con l'uscita di 58 numeri diversi (p = 13,5928%).
Il 50% di probabilità di vedere l'uscita di tutti i 90 numeri si raggiunge con 86 estrazioni, mentre dopo 100 estrazioni c'è il 22,46% di avere esattamente un numero in ritardo (non sortito), il 3,15% che ce ne siano in ritardo 2 e il 74,10% di probabilità che siano usciti tutti e 90.
Infine, ci vogliono 200 estrazioni perché la probabilità di non trovare numeri non estratti sia al 99,9% e 240 affinché la probabilità vada al 99,99%.
Dopo 100 estrazioni (e più in generale dopo un qualsiasi numero n di estrazioni) come si fa a calcolare la probabilità di non avere più nessun numero non estratto, cioè di osservare tutti i 90 numeri usciti in una ruota?
E quindi (per differenza dal 100%) qual è la probabilità che si trovi ancora almeno un ritardatario?
Indico brevemente come realizzare un foglio excel che permette una stima precisa dell'andamento della probabilità di sortita di x qualsiasi dei 90 numeri del lotto in funzione di n estrazioni successive.
- Nelle prime tre righe si pone un titolo esaustivo del lavoro che viene svolto
- Nella riga 5, partendo dalla colonna B fino alla colonna CM, si inseriscono i numeri da 1 a 90
- Nella colonna A, da A6 a esempio A245, si inseriscono i numeri da 1 a 240, che stanno ad indicare il numero delle estrazioni
- Nelle celle delle colonne B C D E, da B6 a E245, vanno inseriti tutti 0, in quanto la probabilità di ottenere 1 o 2 o 3 o 4 numeri già dopo la prima estrazione è ovviamente nulla
- Nella cella F6 deve essere digitato 1, che corrisponde alla probabilità di ottenere 5 numeri dopo 1 estrazione.
Ovviamente, in tutte le celle da G6 a CM6 deve essere inserito 0, in quanto ad ogni estrazione si estraggono 5 numeri, e dopo la prima non è possibile che ce ne siano 6 o di più
- Nella cella F7 si inserisce la formula =5*4*3*2/5273912160*F6
Si fa un copia - incolla sulla stessa colonna F fino a F245. Questa è la probabilità di avere sempre, nelle varie estrazioni successive, la ripetizione degli stessi 5 numeri sortiti alla prima estrazione
- Nella cella G7, attenzione a non sbagliare!, si inserisce questa formula
=(G6*G&5*F&5*E&5*D&5*C&5+F6*5*(90-F&5)*F&5*E&5*D&5*C&5+E6*10*(90-F&5)*(90-E&5)*E&5*D&5*C&5+D6*10*(90-F&5)*(90-E&5)*(90-D&5)*D&5*C&5+C6*5*(90-F&5)*(90-E&5)*(90-D&5)*(90-C&5)*C&5+B6*(90-F&5)*(90-E&5)*(90-D&5)*(90-C&5)*(90-B&5))/5273912160
* Ho dovuto mettere il carattere & anzichè il carattere dollaro, che qui ha scopo diverso e che dovrà invece essere sostituito nel foglio excel
Fare copia-incolla sulla riga fino a CM7
Selezionare da G7 a CM7 e fare copia-incolla fino all'ultima riga G245:CM245
La tabella si riempie di numeri, che corrispondono al valore di probabilità di avere l'uscita della quantità dei numeri indicata nella riga 5 dopo il numero di estrazioni della colonna A.
L'errore dei risultati così ottenuti dipende solo dall'arrotondamento e troncamento dei calcoli fatti da excel (cioè dal numero di cifre significative che excel memorizza e utilizza).
BUON LAVORO!
Nino
E quindi (per differenza dal 100%) qual è la probabilità che si trovi ancora almeno un ritardatario?
Indico brevemente come realizzare un foglio excel che permette una stima precisa dell'andamento della probabilità di sortita di x qualsiasi dei 90 numeri del lotto in funzione di n estrazioni successive.
- Nelle prime tre righe si pone un titolo esaustivo del lavoro che viene svolto
- Nella riga 5, partendo dalla colonna B fino alla colonna CM, si inseriscono i numeri da 1 a 90
- Nella colonna A, da A6 a esempio A245, si inseriscono i numeri da 1 a 240, che stanno ad indicare il numero delle estrazioni
- Nelle celle delle colonne B C D E, da B6 a E245, vanno inseriti tutti 0, in quanto la probabilità di ottenere 1 o 2 o 3 o 4 numeri già dopo la prima estrazione è ovviamente nulla
- Nella cella F6 deve essere digitato 1, che corrisponde alla probabilità di ottenere 5 numeri dopo 1 estrazione.
Ovviamente, in tutte le celle da G6 a CM6 deve essere inserito 0, in quanto ad ogni estrazione si estraggono 5 numeri, e dopo la prima non è possibile che ce ne siano 6 o di più
- Nella cella F7 si inserisce la formula =5*4*3*2/5273912160*F6
Si fa un copia - incolla sulla stessa colonna F fino a F245. Questa è la probabilità di avere sempre, nelle varie estrazioni successive, la ripetizione degli stessi 5 numeri sortiti alla prima estrazione
- Nella cella G7, attenzione a non sbagliare!, si inserisce questa formula
=(G6*G&5*F&5*E&5*D&5*C&5+F6*5*(90-F&5)*F&5*E&5*D&5*C&5+E6*10*(90-F&5)*(90-E&5)*E&5*D&5*C&5+D6*10*(90-F&5)*(90-E&5)*(90-D&5)*D&5*C&5+C6*5*(90-F&5)*(90-E&5)*(90-D&5)*(90-C&5)*C&5+B6*(90-F&5)*(90-E&5)*(90-D&5)*(90-C&5)*(90-B&5))/5273912160
* Ho dovuto mettere il carattere & anzichè il carattere dollaro, che qui ha scopo diverso e che dovrà invece essere sostituito nel foglio excel
Fare copia-incolla sulla riga fino a CM7
Selezionare da G7 a CM7 e fare copia-incolla fino all'ultima riga G245:CM245
La tabella si riempie di numeri, che corrispondono al valore di probabilità di avere l'uscita della quantità dei numeri indicata nella riga 5 dopo il numero di estrazioni della colonna A.
L'errore dei risultati così ottenuti dipende solo dall'arrotondamento e troncamento dei calcoli fatti da excel (cioè dal numero di cifre significative che excel memorizza e utilizza).
BUON LAVORO!
Nino


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo