Esercizio variabile uniforme
il rendimento annuale di un investimento varia tra il -1% ed il 7% e si distribuisce secondo una variabile uniforme. Se vengono investiti 1000 euro, calcolare:
a)la probabilità che dopo un anno l'investimento valga almeno 1050 euro
b)il valore atteso medio dell'investimento dopo un anno
c)la funz. di ripartizione del valore dell'investimento dopo un anno
mi aiutate a risolvere questo esercizio...non so da che parte cominciare!
a)la probabilità che dopo un anno l'investimento valga almeno 1050 euro
b)il valore atteso medio dell'investimento dopo un anno
c)la funz. di ripartizione del valore dell'investimento dopo un anno
mi aiutate a risolvere questo esercizio...non so da che parte cominciare!
Risposte
nessuno che mi possa aiutare???
Non avevo letto il tuo post 
. Da premettere che questi esercizi sono un pò che non li faccio, però voglio cercare ugualmente di esserti utile.
Definisciti la v.a.
$X$=il rendimento annuale di un investimento
Sai che X si distribuisce come una variabile aleatoria uniforme sull'intervallo $[-0.01,0.07]$, ovvero $X sim U(-0.01,0.07)$: una variabile aleatoria uniforme in un intervallo $[a,b]$ ha come funzione di distribuzione
$F_{x}(X)={(0,if x
e $F_{x}(X)=1$ se $x>b$.
Ora non dovresti avere problemi a fare l'esercizio: per il punto 1 quanto vale il rendimento se dopo un anno hai un valore di 1050?
Provaci e fammi sapere dove ti blocchi.
. Da premettere che questi esercizi sono un pò che non li faccio, però voglio cercare ugualmente di esserti utile.Definisciti la v.a.
$X$=il rendimento annuale di un investimento
Sai che X si distribuisce come una variabile aleatoria uniforme sull'intervallo $[-0.01,0.07]$, ovvero $X sim U(-0.01,0.07)$: una variabile aleatoria uniforme in un intervallo $[a,b]$ ha come funzione di distribuzione
$F_{x}(X)={(0,if x
e $F_{x}(X)=1$ se $x>b$.
Ora non dovresti avere problemi a fare l'esercizio: per il punto 1 quanto vale il rendimento se dopo un anno hai un valore di 1050?
Provaci e fammi sapere dove ti blocchi.
grazie mille per la risposta e scusa se ogni tanto chiedo aiuto per qualche esercizio...ma il 12 ho l'esame di statistica e ogni tanto ho qualche difficoltà nel risolvere gli esercizi! Grazie ancora!
Figurati, fin quando posso ho piacere a dare un aiuto. In bocca al lupo per l'esame.
Ciao
Ciao
ho lo stesso esercizio ma nemmeno con l'aiuto lo riesco a fare... e poi
$F(X)=x/(b-a)$ e non $F(X)=(x-a)/(b-a)$.. no?
$F(X)=x/(b-a)$ e non $F(X)=(x-a)/(b-a)$.. no?
in effetti neanche io ho capito come si svolga l'esercizio...
Rappresentate graficamente il problema, forse sarà piu' chiaro. (In BLU la distribuzione)
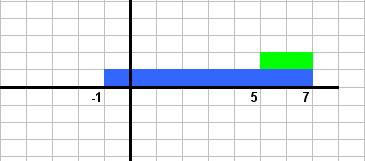
Al punto A si chiede che l'invest. abbia almeno un incremento del 5% (1050 su 1000) (VERDE)
... continuate....
Al punto A si chiede che l'invest. abbia almeno un incremento del 5% (1050 su 1000) (VERDE)
... continuate....
prima faccio
$1000*(1+i)=1050$
$i=5$
poi faccio $Pr(x>=5)=int_5^7fxdx=2/8$
poi per il valore atteso dell'investimento $E(x)=(a+b)/2=3$ ????
e per il punto c) ho 0 idee
$1000*(1+i)=1050$
$i=5$
poi faccio $Pr(x>=5)=int_5^7fxdx=2/8$
poi per il valore atteso dell'investimento $E(x)=(a+b)/2=3$ ????
e per il punto c) ho 0 idee
La funzione di ripartizione della uniforme tra $a$ e $b$ e' giusta come l'ha scritta olaxgabry.
La risposta ad (a) e' 2/8 e non 3/8 (basta contare i quadretti del bel disegno di Umby).
Per (b) il rendimento annuale medio e' 3%, dunque il valore medio dopo un anno e' 1030.
Per (c) e' sempre una variabile uniforme tra 950 e 1070.
La risposta ad (a) e' 2/8 e non 3/8 (basta contare i quadretti del bel disegno di Umby).
Per (b) il rendimento annuale medio e' 3%, dunque il valore medio dopo un anno e' 1030.
Per (c) e' sempre una variabile uniforme tra 950 e 1070.
grazie e correggo il post sopra... come ho fatto a considerarla come una variabile discreta? booooooh
Non mi ero accorto che vi eravate bloccati. Quello che dice Econmax è assolutamente corretto. Una volta calcolata la funzione di ripartizione, l'esercizio è semplice:
1. La probabilità che l'investimento sia almeno di 1050, equivale a calcolare
$P(X>0,05)=1-P(x<=0,05)=1-F_{X}(0,05)=1-[0,05+0,01]/[0,07+0,01]=0,25=1/4$.
2. Il valore medio dell'investimento dopo un anno, equivale a calcolare la media di $X$, ovvero
$E(X)=int_{R}xf_{X}(x)dx=int_{-0,01}^{0,07}x/[0,08] dx=0,03$
3. Niente da aggiungere.
1. La probabilità che l'investimento sia almeno di 1050, equivale a calcolare
$P(X>0,05)=1-P(x<=0,05)=1-F_{X}(0,05)=1-[0,05+0,01]/[0,07+0,01]=0,25=1/4$.
2. Il valore medio dell'investimento dopo un anno, equivale a calcolare la media di $X$, ovvero
$E(X)=int_{R}xf_{X}(x)dx=int_{-0,01}^{0,07}x/[0,08] dx=0,03$
3. Niente da aggiungere.
nel terzo punto $F(X)$ rimane uguale cioè:
$F(X)=(x+0,01)/(0,08)$ per $-0,01<=x<=0,07 $
capisco che varia il capitale su cui calcolare ma tanto i tassi rimangono quelli...
$F(X)=(x+0,01)/(0,08)$ per $-0,01<=x<=0,07 $
capisco che varia il capitale su cui calcolare ma tanto i tassi rimangono quelli...
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo