Calcolo sul lancio dei dadi
Buonasera,
ho bisogno di capire se è possibile calcolare la probabilità di un evento. Mi scuso anticipatamente se alcune delle cose non saranno chiare e\o complete, sono io stesso confuso .
.
Ho 3 dadi:
1) Dado a 6 facce composto dalle seguenti facce: 0 - 0 - 0 - 1 - 1 - 2
2) Dado a 6 facce composto dalle seguenti facce: 0 - 0 - 0 - 1 - 1 - 2
3) Dado a 10 facce composto dalle seguenti facce: 0 - 0 - 0 - 0 - 1 - 1 - 1 - 1 - 2 - 2
Vorrei calcolare la probabilità che lanciandoli tutti e 3 si verifichino le seguenti ipotesi:
1) Il risultato del tiro sia maggiore di 2
2) Il risultato del tiro sia maggiore di 3
(Chiaramente - da profano - ritengo che se imparassi a calcolare una delle due ipotesi riuscirei facilmente a calcolare anche l'altra)
Qualcuno saprebbe venirmi incontro con una spiegazione sul da farsi? Sono riuscito a calcolare la probabilità su 3 dadi identici utilizzando una distribuzione multinomiale, ma il dado a 10 facce mi crea problemi, non so come giostrarmi.
Grazie mille per l'attenzione, ogni tipo di aiuto è gradito.
Saluti!
ho bisogno di capire se è possibile calcolare la probabilità di un evento. Mi scuso anticipatamente se alcune delle cose non saranno chiare e\o complete, sono io stesso confuso
Ho 3 dadi:
1) Dado a 6 facce composto dalle seguenti facce: 0 - 0 - 0 - 1 - 1 - 2
2) Dado a 6 facce composto dalle seguenti facce: 0 - 0 - 0 - 1 - 1 - 2
3) Dado a 10 facce composto dalle seguenti facce: 0 - 0 - 0 - 0 - 1 - 1 - 1 - 1 - 2 - 2
Vorrei calcolare la probabilità che lanciandoli tutti e 3 si verifichino le seguenti ipotesi:
1) Il risultato del tiro sia maggiore di 2
2) Il risultato del tiro sia maggiore di 3
(Chiaramente - da profano - ritengo che se imparassi a calcolare una delle due ipotesi riuscirei facilmente a calcolare anche l'altra)
Qualcuno saprebbe venirmi incontro con una spiegazione sul da farsi? Sono riuscito a calcolare la probabilità su 3 dadi identici utilizzando una distribuzione multinomiale, ma il dado a 10 facce mi crea problemi, non so come giostrarmi.
Grazie mille per l'attenzione, ogni tipo di aiuto è gradito.
Saluti!
Risposte
in questo caso viene più comodo definire la variabile aleatoria risultante dalla somma del lancio dei 3 dadi. Con semplici ragionamenti trovi che[nota]la somma delle probabilità, come in ogni variabile aleatoria, fa 1. Se provi con i valori che ti ho indicato troverai 0.999 perché ho arrotondato i valori delle probabilità[/nota]
$X={{: ( 0 , ;0.100 ),( 1 , ;0.233 ),( 2 , ;0.294),( 3 , ;0.222 ),(4 , ;0.111 ),( 5 , ;0.033 ),( 6 , ;0.006 ) :}$
e quindi per trovare qualunque valore richiesto della somma dei dadi basta che sommi le relative probabilità
Es: $P(X>2)=P(X=3)+P(X=4)+P(X=5)+P(X=6)$
Ps: per interagire in questo forum è richiesto che si inseriscano le formule con l'apposito compilatore in modo da renderle leggibili
$X={{: ( 0 , ;0.100 ),( 1 , ;0.233 ),( 2 , ;0.294),( 3 , ;0.222 ),(4 , ;0.111 ),( 5 , ;0.033 ),( 6 , ;0.006 ) :}$
e quindi per trovare qualunque valore richiesto della somma dei dadi basta che sommi le relative probabilità
Es: $P(X>2)=P(X=3)+P(X=4)+P(X=5)+P(X=6)$
Ps: per interagire in questo forum è richiesto che si inseriscano le formule con l'apposito compilatore in modo da renderle leggibili
Innanzitutto ci tenevo a ringraziarti per la celere risposta e a scusarmi se non ho utilizzato le formule.
A questo punto il calcolo multinomiale che ho fatto risulta una gran perdita di tempo (considerando che ogni volta dovrei prendere in considerazione tutte le combinazioni possibili).
Per quanto riguarda la prima parte della tua risposta, riusciresti a darmi qualche indicazione maggiore in merito all'approccio che hai utilizzato per calcolare le probabilità?
Sull'esempio di risultato 0 penso di aver interpretato che il calcolo fatto prende in considerazione il numero dei risultati "zero" in rapporto al numero di facce totali per ogni dado:
$3/6*3/6*4/10=36/360$
Da qui in poi come proseguo?
Ancora grazie!
A questo punto il calcolo multinomiale che ho fatto risulta una gran perdita di tempo (considerando che ogni volta dovrei prendere in considerazione tutte le combinazioni possibili).
Per quanto riguarda la prima parte della tua risposta, riusciresti a darmi qualche indicazione maggiore in merito all'approccio che hai utilizzato per calcolare le probabilità?
Sull'esempio di risultato 0 penso di aver interpretato che il calcolo fatto prende in considerazione il numero dei risultati "zero" in rapporto al numero di facce totali per ogni dado:
$3/6*3/6*4/10=36/360$
Da qui in poi come proseguo?
Ancora grazie!
prosegui nello stesso modo, facendo tutti i casi; non vedo altra soluzione al momento....ma guarda che è molto semplice, basta moltiplicare le probabilità come hai fatto tu (esagerando ci vorranno 5 minuti in totale)
Ad esempio per $X=3$ (che è uno dei casi più lunghi) ottieni i seguenti eventi elementari: o tutti 1 o tutti diversi:
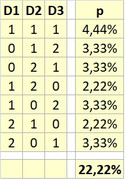
Una volta nota la distribuzione, come sempre, calcoli qualunque probabilità ti venga richiesta ed in modo immediato. Ad esempio una probabilità condizionata:
$P[X<=4|X>2]~~ 89.3%$
Ad esempio per $X=3$ (che è uno dei casi più lunghi) ottieni i seguenti eventi elementari: o tutti 1 o tutti diversi:

Una volta nota la distribuzione, come sempre, calcoli qualunque probabilità ti venga richiesta ed in modo immediato. Ad esempio una probabilità condizionata:
$P[X<=4|X>2]~~ 89.3%$
Grazie alle tue indicazioni sono riuscito a costruire un foglio excel 
Grazie mille tommik, sono veramente contentissimo!
Buona giornata
Grazie mille tommik, sono veramente contentissimo!
Buona giornata


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo