Autobus e passeggeri.....
Salve a tutti sono nuovo e vi scrivo perchè ho un esercizio al quale non sono riuscito a trovare soluzione che è :
Al capolinea salgono sull'autobus 6 persone. Se nelle successive fermate sull'autobus non salgono altri passeggeri e ogni persona sceglie a caso di scendere in una delle 5 fermate, indipendentemente dagli altri passeggeri, quale è la probabilita che l'autobus arrivi vuoto alla quinta fermata? Quale è la probabilita che si svuoti esattamente alla quarta fermata?
La soluzione richiede l'utilizzo della binomiale ma non ho ben capito come.
Grazie.
Al capolinea salgono sull'autobus 6 persone. Se nelle successive fermate sull'autobus non salgono altri passeggeri e ogni persona sceglie a caso di scendere in una delle 5 fermate, indipendentemente dagli altri passeggeri, quale è la probabilita che l'autobus arrivi vuoto alla quinta fermata? Quale è la probabilita che si svuoti esattamente alla quarta fermata?
La soluzione richiede l'utilizzo della binomiale ma non ho ben capito come.
Grazie.
Risposte
Il 30/1 ore 17:59 chiesi a Umby (era una domanda retorica)
Se é così allora stai proponendo la seguente formula ricorsiva:
$S(n+1)=n[S(n)+S(n-1)]$
Giusto?
=========================================
Dalla suddetta formula ricorsiva se ne ricavano subito altre due, che danno numeri molto più piccoli.
1) Pongo $U(n)=(S(n))/((n-1)!) $. Da ciò segue: $U(n+1)=U(n)+\frac{U(n-1)}{n-1}$ , con: $U(1)=0, U(1)=1$.
Per brevità, nel seguito, chiamerò questi numeri "numeri di Umby".
2) Pongo $V(n)=(S(n))/(n!) $. Da ciò segue: $V(n+1)=\frac{nV(n)+V(n-1)}{n+1}$ , con: $V(1)=0, V(2)=1/2$.
Per brevità, nel seguito, chiamerò questi numeri "numeri di Vinc".
Vale il seguente teorema (che so essere vero per altra via, quella che viene dall'hotel a 7 piani e 7 chiavi):
I numeri di Vinc hanno come limite $1/e=0.36788$ circa.
Un primo indizio viene dal fatto che ogni numero di Vinc è la media ponderata dei 2 precedenti e i primi due sono
$V(1)=0$ e$V(2)=0.5$.
----------------------
---> per Umby
Erano queste le formule più pratiche cui alludevi?
O si trattava di una formula chiusa?
Se è la "prima che ho detto", si tratta pur sempre di formule ricorsive, anche se non esplosive come quella per $S(n)$.
Se è "la seconda che ho detto" non mi dare la soluzione: la sto cercando.
Se é così allora stai proponendo la seguente formula ricorsiva:
$S(n+1)=n[S(n)+S(n-1)]$
Giusto?
=========================================
Dalla suddetta formula ricorsiva se ne ricavano subito altre due, che danno numeri molto più piccoli.
1) Pongo $U(n)=(S(n))/((n-1)!) $. Da ciò segue: $U(n+1)=U(n)+\frac{U(n-1)}{n-1}$ , con: $U(1)=0, U(1)=1$.
Per brevità, nel seguito, chiamerò questi numeri "numeri di Umby".
2) Pongo $V(n)=(S(n))/(n!) $. Da ciò segue: $V(n+1)=\frac{nV(n)+V(n-1)}{n+1}$ , con: $V(1)=0, V(2)=1/2$.
Per brevità, nel seguito, chiamerò questi numeri "numeri di Vinc".
Vale il seguente teorema (che so essere vero per altra via, quella che viene dall'hotel a 7 piani e 7 chiavi):
I numeri di Vinc hanno come limite $1/e=0.36788$ circa.
Un primo indizio viene dal fatto che ogni numero di Vinc è la media ponderata dei 2 precedenti e i primi due sono
$V(1)=0$ e$V(2)=0.5$.
----------------------
---> per Umby
Erano queste le formule più pratiche cui alludevi?
O si trattava di una formula chiusa?
Se è la "prima che ho detto", si tratta pur sempre di formule ricorsive, anche se non esplosive come quella per $S(n)$.
Se è "la seconda che ho detto" non mi dare la soluzione: la sto cercando.
Ci ho lavorato 3 ore, ma sono riuscito a tirar fuori solo un risultato.
La così detta "funzione generatrice" dei miei "numeri di Vinc" è:
$F(z)=\frac{e^-z}{1-z} -1= \sum_1^\inftyV_kz^k.
Moltiplicando poi i seguenti sviluppi di McLaurin
$e^(-z)= 1 - z +(z^2)/(2!)-(z^3)/(3!)+(z^4)/(4!) - .....$
$1/(1-z) = 1 + z + z^2 + z^3 + z^4 + ....
si ottiene lo sviluppo in serie di F(z) che ha come coefficienti le quantità
$a_k=1/2! - 1/3! + 1/4! - 1/5! + ----- \pm 1/k!$
Queste quantità coincidono quindi con i "numeri di Vinc" che tendono perciò a $1/e$.
Ma abbiamo ottenuto per altra via un'informazione già nota e la formula di calcolo ottenuta è sì chiusa,
ma non è più semplice di quella da me scritta in un intervento precedente.
Pertanto mi arrendo e chiedo ad Umby di dirmi se sa qualcosa di più in merito.
Mi riferisco al suo annuncio che riporto di seguito:
>Umby scripsit (31 gennaio, ore 11:53):
>Sappi che durante la "generazione" di questa formula (e proprio in virtu' dell'analisi di come si comportavano i numeri della >serie), [mi] si è presentato davanti un metodo ancora piu' facile, che riduce di molto i calcoli, e che la rende piu semplice.
Attendo la rivelazione del tuo metodo.
La così detta "funzione generatrice" dei miei "numeri di Vinc" è:
$F(z)=\frac{e^-z}{1-z} -1= \sum_1^\inftyV_kz^k.
Moltiplicando poi i seguenti sviluppi di McLaurin
$e^(-z)= 1 - z +(z^2)/(2!)-(z^3)/(3!)+(z^4)/(4!) - .....$
$1/(1-z) = 1 + z + z^2 + z^3 + z^4 + ....
si ottiene lo sviluppo in serie di F(z) che ha come coefficienti le quantità
$a_k=1/2! - 1/3! + 1/4! - 1/5! + ----- \pm 1/k!$
Queste quantità coincidono quindi con i "numeri di Vinc" che tendono perciò a $1/e$.
Ma abbiamo ottenuto per altra via un'informazione già nota e la formula di calcolo ottenuta è sì chiusa,
ma non è più semplice di quella da me scritta in un intervento precedente.
Pertanto mi arrendo e chiedo ad Umby di dirmi se sa qualcosa di più in merito.
Mi riferisco al suo annuncio che riporto di seguito:
>Umby scripsit (31 gennaio, ore 11:53):
>Sappi che durante la "generazione" di questa formula (e proprio in virtu' dell'analisi di come si comportavano i numeri della >serie), [mi] si è presentato davanti un metodo ancora piu' facile, che riduce di molto i calcoli, e che la rende piu semplice.
Attendo la rivelazione del tuo metodo.
Ti avevo già accennato al fatto che questa semplificazione era apparsa durante la visione della tabella da me prodotta, pertanto non si tratta di una formula cosi come la definisci "chiusa".
Ritorno di nuovo all'immagine della tabella:
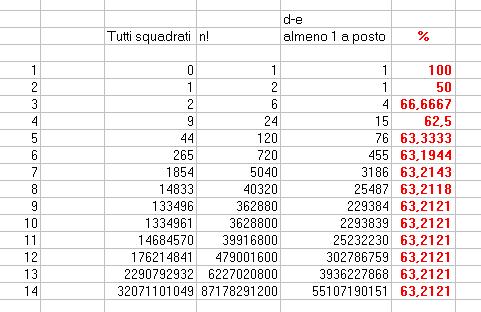
Nel precedente mio intervento ho calcolato la formula "Tutti squadrati" (prima colonna), nella seconda avevo (N!), e nella terza la differenza (almeno 1 al suo posto).
Non mi sono immediatamente accorto che la formula applicata alla prima colonna puo' essere presa (così com'è) ed applicarla direttamente alla terza colonna. Pertanto stabilito il primo elemento (1), ed il secondo elemento (1), dal terzo in poi cadono in cascata tutti gli altri 4 = (3 - 1) * (1 + 1), ed ancora 15 = (4 - 1) * (4 + 1) .......
Così facendo calcolo direttamente il dato che cercavo, evitando due inutili passaggi.
Curiosità: questa formula la definerei semi-artigianale. Ovvero per funzionare è necessario calcolare almeno i primi due elementi (D1 e D2), dopodichè è possibile dal D3 in poi ciclizzarla. E' altresì vero che proprio questi due elementi sono facilmente calcolabili (anche intuitivamente)
Ciao.
Ritorno di nuovo all'immagine della tabella:

Nel precedente mio intervento ho calcolato la formula "Tutti squadrati" (prima colonna), nella seconda avevo (N!), e nella terza la differenza (almeno 1 al suo posto).
Non mi sono immediatamente accorto che la formula applicata alla prima colonna puo' essere presa (così com'è) ed applicarla direttamente alla terza colonna. Pertanto stabilito il primo elemento (1), ed il secondo elemento (1), dal terzo in poi cadono in cascata tutti gli altri 4 = (3 - 1) * (1 + 1), ed ancora 15 = (4 - 1) * (4 + 1) .......
Così facendo calcolo direttamente il dato che cercavo, evitando due inutili passaggi.
Curiosità: questa formula la definerei semi-artigianale. Ovvero per funzionare è necessario calcolare almeno i primi due elementi (D1 e D2), dopodichè è possibile dal D3 in poi ciclizzarla. E' altresì vero che proprio questi due elementi sono facilmente calcolabili (anche intuitivamente)
Ciao.
Ah, quindi quasi nulla di nuovo. La cosa andava però notata, ed eccone la dimostrazione rigorosa senza tabelle EXCEL.
La relazione ricorsiva valida per la 1.a colonna, da te segnalata qualche giorno fa, era
S(n+1)=n[S(n)+S(n-1)]
Considera ora il complemento di S(n) a n! cioè S(n)=n!-T(n), cioè T(n) è la tua terza colonna definita come la differenza fra la seconda, che é n! , e la prima, che è S(n).
Sostituendo ora nella (1) si ha
(n+1)! -T(n+1) = n( n! - T(n) + (n-1)! - T(n-1)
I tre termini coi fattoriali si elidono subito e si ottiene
T(n+1) = n( T(n) + T(n-1) ), la stessa relazione ricorsiva soddisfatta dagli S(n)!
L'unica cosa che cambia sono le 2 "condizioni iniziali"
E' proprio il caso di dire con Jakob Bernoulli : "Eadem mutata resurgo!"
Questa epigrafe, che si riferiva alla sua spirale logaritmica, se la fece scalpellare sulla lapide tombale, ma fu sfortunato! Lo scalpellino non riuscì a scolpire sulla pietra altro che una spirale di Archimede, una spirale meno fascinosa della sua. Per inciso Archimede invece non fece in tempo a decidere l'epigrafe da scolpire sulla sua tomba, anche se si sa che in punto di morte (prima di essere trucidato da un soldato romano) fece in tempo a dire : "Noli turbare circulos meos!" frase che, da buon analfabeta, il legionario tradusse malamente come: "Non mi scassare 'e ppalle!"
Cito questo aneddoti perché so quanto ami le frasi in latino!
La relazione ricorsiva valida per la 1.a colonna, da te segnalata qualche giorno fa, era
S(n+1)=n[S(n)+S(n-1)]
Considera ora il complemento di S(n) a n! cioè S(n)=n!-T(n), cioè T(n) è la tua terza colonna definita come la differenza fra la seconda, che é n! , e la prima, che è S(n).
Sostituendo ora nella (1) si ha
(n+1)! -T(n+1) = n( n! - T(n) + (n-1)! - T(n-1)
I tre termini coi fattoriali si elidono subito e si ottiene
T(n+1) = n( T(n) + T(n-1) ), la stessa relazione ricorsiva soddisfatta dagli S(n)!
L'unica cosa che cambia sono le 2 "condizioni iniziali"
E' proprio il caso di dire con Jakob Bernoulli : "Eadem mutata resurgo!"
Questa epigrafe, che si riferiva alla sua spirale logaritmica, se la fece scalpellare sulla lapide tombale, ma fu sfortunato! Lo scalpellino non riuscì a scolpire sulla pietra altro che una spirale di Archimede, una spirale meno fascinosa della sua. Per inciso Archimede invece non fece in tempo a decidere l'epigrafe da scolpire sulla sua tomba, anche se si sa che in punto di morte (prima di essere trucidato da un soldato romano) fece in tempo a dire : "Noli turbare circulos meos!" frase che, da buon analfabeta, il legionario tradusse malamente come: "Non mi scassare 'e ppalle!"
Cito questo aneddoti perché so quanto ami le frasi in latino!
"seascoli":
L'unica cosa che cambia sono le 2 "condizioni iniziali"
Anche a me, questa condizione non andava giù. Ho trovato una seconda formula (anche più carina) che ne fa a meno.
Il fatto che queste formule siano ricorsive è giusto che lo siano. Ricordiamoci che ci sta di mezzo la "fattorialità" che di per se, è una formula ricorsiva. Noi la scriviamo semplicemente con un "!", ma dietro cosa c'è ?
P.s. La pubblico nell'altro topic.
Ripeto: quando hai una formula chiusa, per giunta semplice, ogni formula ricorsiva che dà la stessa risposta è, nel migliore dei casi, pleonastica. Ma al solito "de gustibus, non disputandum ...", tanto per usare una lingua a te molto simpatica. 




 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo