Autobus e passeggeri.....
Salve a tutti sono nuovo e vi scrivo perchè ho un esercizio al quale non sono riuscito a trovare soluzione che è :
Al capolinea salgono sull'autobus 6 persone. Se nelle successive fermate sull'autobus non salgono altri passeggeri e ogni persona sceglie a caso di scendere in una delle 5 fermate, indipendentemente dagli altri passeggeri, quale è la probabilita che l'autobus arrivi vuoto alla quinta fermata? Quale è la probabilita che si svuoti esattamente alla quarta fermata?
La soluzione richiede l'utilizzo della binomiale ma non ho ben capito come.
Grazie.
Al capolinea salgono sull'autobus 6 persone. Se nelle successive fermate sull'autobus non salgono altri passeggeri e ogni persona sceglie a caso di scendere in una delle 5 fermate, indipendentemente dagli altri passeggeri, quale è la probabilita che l'autobus arrivi vuoto alla quinta fermata? Quale è la probabilita che si svuoti esattamente alla quarta fermata?
La soluzione richiede l'utilizzo della binomiale ma non ho ben capito come.
Grazie.
Risposte
Belle formule quelle che hai dato, per quanto io le avrei scritte nella forma generale
grazie.
non ci vuole molto, anzi ci vuole molto meno perché vengono "esclusi" i calcoli numerici.
basta formulare i problemi in forma più generale.
metodi alternativi?
non ci vuole molto, anzi ci vuole molto meno perché vengono "esclusi" i calcoli numerici.
basta formulare i problemi in forma più generale.
metodi alternativi?
Li ho provati, ma sono inferiori quanto a potenza risolutiva.
Ho esplorato questo approccio.
Sia $f$ una fermata $(f = 1, 2, 3, ..., F)$ e $n(f)$ indichi il numero di passeggeri che scendono alla fermata $f$.
Allora i modi possibili per $P$ passeggeri di scendere dall'autobus lungo un tragitto con $F$ fermate sono le soluzioni dell'equazione diofantea:
(1) $n_1+n_2+......+n_F=P$
E' noto che il numero di soluzioni senza vincoli di sorta è $((P+F-1),(P))$.
Analogamente è facile calcolare il numero di soluzioni con i vincoli $n_k>0$ o $0<=n_k<=1$, che servirebbero a risolvere entrambi i quesiti da me posti ...... se non fosse per il dannato fatto che i casi possibili non sono equiprobabili!
In effetti ogni soluzione della (1) va pesata con il fattore di Leibniz $(P!)/(n_1!n_2!....n_F!)$ e le cose diventano meno eleganti.
Si ottiene comunque anche così la risposta esatta (almeno stando alle verifiche che ho fatto in casi particolari) ma in modo meno elegante e diretto che con le tue formule. L'unico difetto di quest'ultime, se di difetto si può parlare, è la scarsa comprensibilità per i non esperti. M'immagino per esempio la reazione di Umby davanti alla "sparata" ex abrupto dei numeri di Stirling di 2.a specie!
Ho esplorato questo approccio.
Sia $f$ una fermata $(f = 1, 2, 3, ..., F)$ e $n(f)$ indichi il numero di passeggeri che scendono alla fermata $f$.
Allora i modi possibili per $P$ passeggeri di scendere dall'autobus lungo un tragitto con $F$ fermate sono le soluzioni dell'equazione diofantea:
(1) $n_1+n_2+......+n_F=P$
E' noto che il numero di soluzioni senza vincoli di sorta è $((P+F-1),(P))$.
Analogamente è facile calcolare il numero di soluzioni con i vincoli $n_k>0$ o $0<=n_k<=1$, che servirebbero a risolvere entrambi i quesiti da me posti ...... se non fosse per il dannato fatto che i casi possibili non sono equiprobabili!
In effetti ogni soluzione della (1) va pesata con il fattore di Leibniz $(P!)/(n_1!n_2!....n_F!)$ e le cose diventano meno eleganti.
Si ottiene comunque anche così la risposta esatta (almeno stando alle verifiche che ho fatto in casi particolari) ma in modo meno elegante e diretto che con le tue formule. L'unico difetto di quest'ultime, se di difetto si può parlare, è la scarsa comprensibilità per i non esperti. M'immagino per esempio la reazione di Umby davanti alla "sparata" ex abrupto dei numeri di Stirling di 2.a specie!
due noticine.
mentre ero "tranquillamente" seduta sul divano (davanti al televisore e con le pentole sul fuoco), con carta, penna e calcolatrice scientifica, sono riuscita a ricavare S(15,10) ricorsivamente.
dopo, però, ho deciso di usare uno strumento più efficace, che tra l'altro piace tanto ad Umby, Excel, e mi sono sorpresa che, a parte le caselle base, ho avuto bisogno di scrivere un'unica formula per ottenere il Triangolo di Stirling della grandezza desiderata (per praticità mi sono fermata alla casella S(30,20), il cui valore, per la cronaca, viene riportato in forma esponenziale: 5.82E+17).
sempre per la cronaca, il tuo tentativo di soluzione mi fa pensare al mio tentativo per risolvere l'altro quesito (quello delle 7 chiavi e delle 7 cameriere).
molto probabilmente mi perdo qualche caso, oppure sbaglio qualche calcolo, perché non mi ritrovo passando dalla teoria alla pratica. chiedo conferma di una questione generale: è vero che 7 può essere scritto in 64 modi come somma di uno o più addendi? in realtà mi sto risondendo da sola: sì e no. sono le "composizioni", dove però se ci sono dei numeri ripetuti, conta l'ordine degli addendi. invece, in un altro "conteggio" che ho utilizzato per lo stesso esercizio, ho utilizzato i coefficienti multinomiali, divisi però in modo da non conteggiare più volte la stessa composizione.
se pensi di potermi correggere e/o darmi qualche indizio, ti ringrazio anticipatamente.
ciao.
mentre ero "tranquillamente" seduta sul divano (davanti al televisore e con le pentole sul fuoco), con carta, penna e calcolatrice scientifica, sono riuscita a ricavare S(15,10) ricorsivamente.
dopo, però, ho deciso di usare uno strumento più efficace, che tra l'altro piace tanto ad Umby, Excel, e mi sono sorpresa che, a parte le caselle base, ho avuto bisogno di scrivere un'unica formula per ottenere il Triangolo di Stirling della grandezza desiderata (per praticità mi sono fermata alla casella S(30,20), il cui valore, per la cronaca, viene riportato in forma esponenziale: 5.82E+17).
sempre per la cronaca, il tuo tentativo di soluzione mi fa pensare al mio tentativo per risolvere l'altro quesito (quello delle 7 chiavi e delle 7 cameriere).
molto probabilmente mi perdo qualche caso, oppure sbaglio qualche calcolo, perché non mi ritrovo passando dalla teoria alla pratica. chiedo conferma di una questione generale: è vero che 7 può essere scritto in 64 modi come somma di uno o più addendi? in realtà mi sto risondendo da sola: sì e no. sono le "composizioni", dove però se ci sono dei numeri ripetuti, conta l'ordine degli addendi. invece, in un altro "conteggio" che ho utilizzato per lo stesso esercizio, ho utilizzato i coefficienti multinomiali, divisi però in modo da non conteggiare più volte la stessa composizione.
se pensi di potermi correggere e/o darmi qualche indizio, ti ringrazio anticipatamente.
ciao.
Per come l'hai messa, ci sono infiniti modi di rappresentare 7 come somma di più addendi.
Allora delle due l'una:
--- o non si può usare zero come addendo
--- oppure devi stabilire un tetto al numero degli addendi (per es. 7 in 7 addendi , o, che so?, in 12, fai tu)
Qualunque di questi vincoli scegli, ho la formula esplicita che conta le "scomposizioni" di 7 e, se occorre, anche una dimostrazione. Non so come hai ricavato quel 64.
Ovviamente due "scomposizioni" di un numero N in k addendi vanno riguardate distinte anche se differiscono solo per l'ordine degli addendi.
A te la scelta!
Allora delle due l'una:
--- o non si può usare zero come addendo
--- oppure devi stabilire un tetto al numero degli addendi (per es. 7 in 7 addendi , o, che so?, in 12, fai tu)
Qualunque di questi vincoli scegli, ho la formula esplicita che conta le "scomposizioni" di 7 e, se occorre, anche una dimostrazione. Non so come hai ricavato quel 64.
Ovviamente due "scomposizioni" di un numero N in k addendi vanno riguardate distinte anche se differiscono solo per l'ordine degli addendi.
A te la scelta!
per ottenere 64 ho utilizzato la formula $((n-1),(k-1))$che dà le composizioni di n in k parti, e quella del binomio di Newton:
$Sigma_(i=0)^6\((6),(i))=2^6$
mentre, nel calcolo diretto, avevo provato a suddividere i casi in più modi, ottenendo in un'occasione 415 casi (penso quelli favorevoli, ma non ritrovo il numero di quelli non favorevoli) ed in un'altra occasione 2045 casi totali (che invece avrebbero dovuto essere 7! = 5040) di cui 1541 favorevoli e 504 contrari.
si considerino i cicli di lunghezza k non esprimibili come prodotto di cicli più brevi. se $alpha=((1,2,3, ... , k),(a_1,a_2,a_3, ... , a_k))$ è una permutazione che genera tale ciclo, allora $alpha^k="identita'"$, mentre $(k-1)!$ sono le permutazioni senza elementi fissi? chiedo conferma.
sicuramente tra le permutazioni senza elementi fissi ci sono anche quelle esprimibili come prodotto di cicli di lunghezze maggiori di 1 ma minori di k, mentre quelle che non sono esprimibili come prodotto di cicli più brevi sono "solo" $k-1$ ? io credo di no. c'è un modo per collegare i due risultati?
spero che si capisca quello che chiedo. ringrazio anticipatamente. ciao.
$Sigma_(i=0)^6\((6),(i))=2^6$
mentre, nel calcolo diretto, avevo provato a suddividere i casi in più modi, ottenendo in un'occasione 415 casi (penso quelli favorevoli, ma non ritrovo il numero di quelli non favorevoli) ed in un'altra occasione 2045 casi totali (che invece avrebbero dovuto essere 7! = 5040) di cui 1541 favorevoli e 504 contrari.
si considerino i cicli di lunghezza k non esprimibili come prodotto di cicli più brevi. se $alpha=((1,2,3, ... , k),(a_1,a_2,a_3, ... , a_k))$ è una permutazione che genera tale ciclo, allora $alpha^k="identita'"$, mentre $(k-1)!$ sono le permutazioni senza elementi fissi? chiedo conferma.
sicuramente tra le permutazioni senza elementi fissi ci sono anche quelle esprimibili come prodotto di cicli di lunghezze maggiori di 1 ma minori di k, mentre quelle che non sono esprimibili come prodotto di cicli più brevi sono "solo" $k-1$ ? io credo di no. c'è un modo per collegare i due risultati?
spero che si capisca quello che chiedo. ringrazio anticipatamente. ciao.
"adaBTTLS":
per ottenere 64 ho utilizzato la formula $((n-1),(k-1))$che dà le composizioni di n in k parti, e quella del binomio di Newton:
$Sigma_(i=0)^6\((6),(i))=2^6$
facendo una breve indagine sembra che il 64, possa ricavarsi anche dal triangolo di tartaglia, cosi' facendo si possono conoscere anche come sono distribuite le sommatorie di n elementi.
Nel caso del 7 si ha:
1 - 6 - 15 - 20 - 15 - 6 - 1
che sono rispettivamente i modi per sommare 1 o 2 ..... 7 numeri.
sì, Umby, questi numeri tornano, anche se non vedo come mi possa aiutare il fatto che ad esempio 7=4+2+1 vada contato 6 volte perché si può scrivere anche permutando gli addendi, mentre magari non devo considerare come scelgo i 4,2,1 elementi da abbinare (cosa che invece mi dicono i coefficienti multinomiali).
comunque nel problema generale serviva a ridurre il conteggio delle permutazioni senza punti fissi al conteggio dei cicli di lunghezza k: conosci un metodo per arrivarci? se è ad esempio più semplice contare le permutazioni con o senza ripetizioni, allora è più utile considerare solo le 6 composizioni in due parti.
ciao.
comunque nel problema generale serviva a ridurre il conteggio delle permutazioni senza punti fissi al conteggio dei cicli di lunghezza k: conosci un metodo per arrivarci? se è ad esempio più semplice contare le permutazioni con o senza ripetizioni, allora è più utile considerare solo le 6 composizioni in due parti.
ciao.
La formula $((n-1),(k-1))$ è corretta solo se fra gli addendi non può figurare lo zero e se, ripeto, due scomposizioni si riguardano distinte anche solo per l'ordine. E' così che conviene definirle!
Se vi interessa, ho una dimostrazione per una formula molto più generale che dà il numero delle scomposizioni di n in k addendi, ciascuno dei quali sia non inferiore a m (m
$S_0(n,k)=((n+k-1),(n))$, cioè il numero delle combinazioni con ripetizione di n oggetti a n a n.
Lo sapete perché?
Si ha inoltre come già sapete:
$S_1(n,k)=((n-1),(k-1))$
Vi dicevo che ho derivato (anni fa) anche la formula per $S_m(n,k)$, se vi può interessare...
Tornando al problema di scomporre 7 in addendi, senza precisare quanti, e senza precisare se si possono usare addendi nulli, torno a dire che le scomposizioni in parola sono ovviamente infinite.
Tuttavia non vedo proprio come il numero delle scomposizioni di 7 possa avere, anche lontanamente, a che fare col problema delle 7 chiavi da me formulato (e risolto) altrove.
Se vi interessa, ho una dimostrazione per una formula molto più generale che dà il numero delle scomposizioni di n in k addendi, ciascuno dei quali sia non inferiore a m (m
$S_0(n,k)=((n+k-1),(n))$, cioè il numero delle combinazioni con ripetizione di n oggetti a n a n.
Lo sapete perché?
Si ha inoltre come già sapete:
$S_1(n,k)=((n-1),(k-1))$
Vi dicevo che ho derivato (anni fa) anche la formula per $S_m(n,k)$, se vi può interessare...
Tornando al problema di scomporre 7 in addendi, senza precisare quanti, e senza precisare se si possono usare addendi nulli, torno a dire che le scomposizioni in parola sono ovviamente infinite.
Tuttavia non vedo proprio come il numero delle scomposizioni di 7 possa avere, anche lontanamente, a che fare col problema delle 7 chiavi da me formulato (e risolto) altrove.
Ada scripsit:
(k-1)! sono le permutazioni senza elementi fissi? chiedo conferma.
sicuramente tra le permutazioni senza elementi fissi ci sono anche quelle esprimibili come prodotto di cicli di lunghezze maggiori di 1 ma minori di k, mentre quelle che non sono esprimibili come prodotto di cicli più brevi sono "solo" k-1 ? io credo di no. c'è un modo per collegare i due risultati?
spero che si capisca quello che chiedo. ringrazio anticipatamente. ciao.
===============================================
Non non capisco.
Cosa intendi esattamente per "permutazioni senza elementi fissi"?
Forse "permutazioni che non lascian alcun elemento al loro posto?"
Le permutazioni tout court di n elementi non fissano in anticipo nessun elemento.
Ciò non toglie che in (n-1)! di esse un dato elemento rimane fisso al suo posto.
Analogamente ci sono (n-k)! permutazioni che lasciano k elementi prefissati al loro posto (senza alcun vincolo per tutti gli altri).
Il numero delle permutazioni di n elementi che non lasciano alcun elemento al suo posto, se ci rifletti con calma, sono:
$n! -((n),(1))(n-1)!+((n),(2))(n-2)! -((n),(3))(n-3)! + ..... $ etc. fino a 1!
Questo ti dà i casi favorevoli nel problema delle 7 chiavi, se la probabilità da calcolare è quella complementare cioè:
P(0)=Prob. che nessuna chiave risulti essere quella giusta
Basterà poi sottrarre P(0) da 1 per avere la Prob. che almeno 1 chiave vada bene, che è la probabilità richiesta nel testo originale (quesito del "portiere d'albergo").
Non capisco inoltre che cosa c'entrano le "permutazioni cicliche".
Così non fai che complicare inutilmente il problema, secondo me!
(k-1)! sono le permutazioni senza elementi fissi? chiedo conferma.
sicuramente tra le permutazioni senza elementi fissi ci sono anche quelle esprimibili come prodotto di cicli di lunghezze maggiori di 1 ma minori di k, mentre quelle che non sono esprimibili come prodotto di cicli più brevi sono "solo" k-1 ? io credo di no. c'è un modo per collegare i due risultati?
spero che si capisca quello che chiedo. ringrazio anticipatamente. ciao.
===============================================
Non non capisco.
Cosa intendi esattamente per "permutazioni senza elementi fissi"?
Forse "permutazioni che non lascian alcun elemento al loro posto?"
Le permutazioni tout court di n elementi non fissano in anticipo nessun elemento.
Ciò non toglie che in (n-1)! di esse un dato elemento rimane fisso al suo posto.
Analogamente ci sono (n-k)! permutazioni che lasciano k elementi prefissati al loro posto (senza alcun vincolo per tutti gli altri).
Il numero delle permutazioni di n elementi che non lasciano alcun elemento al suo posto, se ci rifletti con calma, sono:
$n! -((n),(1))(n-1)!+((n),(2))(n-2)! -((n),(3))(n-3)! + ..... $ etc. fino a 1!
Questo ti dà i casi favorevoli nel problema delle 7 chiavi, se la probabilità da calcolare è quella complementare cioè:
P(0)=Prob. che nessuna chiave risulti essere quella giusta
Basterà poi sottrarre P(0) da 1 per avere la Prob. che almeno 1 chiave vada bene, che è la probabilità richiesta nel testo originale (quesito del "portiere d'albergo").
Non capisco inoltre che cosa c'entrano le "permutazioni cicliche".
Così non fai che complicare inutilmente il problema, secondo me!
grazie delle due risposte.
riguardo alle varie formule che proponi, sicuramente, essendo diverse, di qualcuna ho la dimostrazione e di qualcun'altra no, comunque puoi postare quelle che ritieni più interessanti per me ma anche per altri utenti.
sul dubbio che ho posto in maniera poco chiara, in qualche modo mi sto rispondendo da sola.
non sono lontana da una soluzione alternativa.
quando ce l'avrò, forse sarò in grado di selezionare la parte dei miei ragionamenti precedenti non completamente campata in aria, e potrò aprire al riguardo un altro oggetto di discussione.
per ora forse posso chiarire solo con questo semplice esempio:
se dalla permutazione "principale" di un insieme di tre lementi, cioè 1-2-3 passo a 2-3-1 con un ciclo di lunghezza 3, questo ciclo al quadrato mi porta a 3-1-2, mentre al cubo mi porta all'identità. quindi partendo da una particolare permutazione ciclica di ordine 3 ottengo 2 "permutazioni che non lascian alcun elemento al loro posto". se fosse vero anche per i cicli di lunghezza superiore (però ho controllato che non è così, almeno non nel conteggio elementare), allora certo che servirebbero i modi di decomporre il numero 7: il terribile problema diventerebbe un giochino da ragazzi!
a presto. ciao.
riguardo alle varie formule che proponi, sicuramente, essendo diverse, di qualcuna ho la dimostrazione e di qualcun'altra no, comunque puoi postare quelle che ritieni più interessanti per me ma anche per altri utenti.
sul dubbio che ho posto in maniera poco chiara, in qualche modo mi sto rispondendo da sola.
non sono lontana da una soluzione alternativa.
quando ce l'avrò, forse sarò in grado di selezionare la parte dei miei ragionamenti precedenti non completamente campata in aria, e potrò aprire al riguardo un altro oggetto di discussione.
per ora forse posso chiarire solo con questo semplice esempio:
se dalla permutazione "principale" di un insieme di tre lementi, cioè 1-2-3 passo a 2-3-1 con un ciclo di lunghezza 3, questo ciclo al quadrato mi porta a 3-1-2, mentre al cubo mi porta all'identità. quindi partendo da una particolare permutazione ciclica di ordine 3 ottengo 2 "permutazioni che non lascian alcun elemento al loro posto". se fosse vero anche per i cicli di lunghezza superiore (però ho controllato che non è così, almeno non nel conteggio elementare), allora certo che servirebbero i modi di decomporre il numero 7: il terribile problema diventerebbe un giochino da ragazzi!
a presto. ciao.
"seascoli":
Il numero delle permutazioni di n elementi che non lasciano alcun elemento al suo posto, se ci rifletti con calma, sono:
$n! -((n),(1))(n-1)!+((n),(2))(n-2)! -((n),(3))(n-3)! + ..... $ etc. fino a 1!
mi ci trovo con questa formula, anche facendo un ragionamento al contrario
partendo da n=1 il numero di elementi che non possono essere al loro posto è pari a 0 (nel senso che non puo' non essere al suo posto, considerato che è unico)
se invece si considera n=2, ci potrebbe essere una condizione ovvero che i due elementi si invertono
per n=3 ci sono 2 condizioni ovvero la 2-3-1, e la 3-2-1 su 6 (n!)
per n=4 sono 9 (pari al prodotto di n-1(la somma dei due precedenti)) $(4-1)*(2+1)$
e cosi via...
si raggiunge il 7 con 1854 su 5040 (7!)
La probabilità richiesta pertanto è:
$3186/5040$=63,2%$
Trovata la formula, ciclizzandola fino a 14, possiamo vedere le % che si "stabilizzano" 
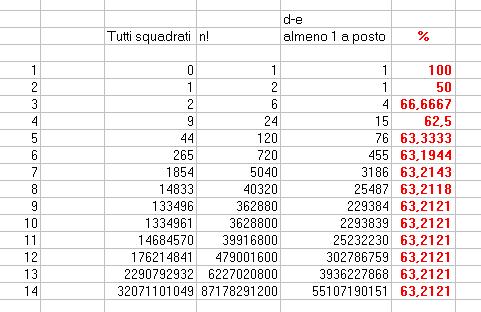

Se vai al mio argomento"Le (terribili) conseguenze dell'amore" scoprirai anche quanto vale tale limite:
Ripeto la traccia in forma di filastrocca:
Ai modesti e vanitosi, ai saccenti e timorosi dò, cantando gaio ritmo, logaritmo!
Ripeto la traccia in forma di filastrocca:
Ai modesti e vanitosi, ai saccenti e timorosi dò, cantando gaio ritmo, logaritmo!
"seascoli":
Se vai al mio argomento"Le (terribili) conseguenze dell'amore" scoprirai anche quanto vale tale limite:
appena visto. avevo gia' letto quel topic.
vedo che usando una strada, completamente diversa dalla tua, sia giunto allo stesso risultato.
Umby scripsit:
per n=4 sono 9, pari al prodotto di n-1 per la somma dei due precedenti ...
===============================================
Che intendi per "i due precedenti"?
Per esempio: per n=5, cosa scrivi: (5-1)(9+2) ?
Se é così allora stai proponendo la seguente formula ricorsiva:
$S(n) = (n-1)[S(n-1) + S(n-2)]$
Giusto?
Se questa è la formula da te trovata, non so ancora se é giusta (te lo dico dopo che rispondi alla mia domanda), ma ho da dire subito questo:
Chi si accontenta di una formula ricorsiva quando ce n'è una esplicita,
è come chi si piega a raccogliere i fichi caduti per terra quando ce ne sono a bizzeffe sulla pianta!
Tra l'altro, per calcolare ad esempio la risposta per N=237, devi prima calcolare tutti i 236 valori precedenti!
Masochismo puro, se lì a portata di mano c'è una formula esplicita.
per n=4 sono 9, pari al prodotto di n-1 per la somma dei due precedenti ...
===============================================
Che intendi per "i due precedenti"?
Per esempio: per n=5, cosa scrivi: (5-1)(9+2) ?
Se é così allora stai proponendo la seguente formula ricorsiva:
$S(n) = (n-1)[S(n-1) + S(n-2)]$
Giusto?
Se questa è la formula da te trovata, non so ancora se é giusta (te lo dico dopo che rispondi alla mia domanda), ma ho da dire subito questo:
Chi si accontenta di una formula ricorsiva quando ce n'è una esplicita,
è come chi si piega a raccogliere i fichi caduti per terra quando ce ne sono a bizzeffe sulla pianta!
Tra l'altro, per calcolare ad esempio la risposta per N=237, devi prima calcolare tutti i 236 valori precedenti!
Masochismo puro, se lì a portata di mano c'è una formula esplicita.
Mahhhh.... 
Non capisco questo tuo continuo atteggiamento di sfida, presente ormai in tutti i tuoi interventi.
Il forum non è una competizione! Ognuno contribuisce nel modo che ritiene opportuno.
Detto cio',
il procedimento da me proposto, mi ha permesso di visionare in tempi brevissimi l'andamento della percentuale con il crescere di n.
Ho impostato la formula sul primo rigo, e trascinando in basso la stessa mi sono apparsi i valori (peraltro che coincidevano con i tuoi, vedi altro topic).
La tua soluzione ti piace di piu' ? Bene ... Terminato questo topic, non verrà mai piu ricordata da nessuno (ne la mia, ne la tua... )
)
Leggendo che hai dei dubbi sulla formula, ti mando il file completo.
Link
Non capisco questo tuo continuo atteggiamento di sfida, presente ormai in tutti i tuoi interventi.
Il forum non è una competizione! Ognuno contribuisce nel modo che ritiene opportuno.
Detto cio',
il procedimento da me proposto, mi ha permesso di visionare in tempi brevissimi l'andamento della percentuale con il crescere di n.
Ho impostato la formula sul primo rigo, e trascinando in basso la stessa mi sono apparsi i valori (peraltro che coincidevano con i tuoi, vedi altro topic).
La tua soluzione ti piace di piu' ? Bene ... Terminato questo topic, non verrà mai piu ricordata da nessuno (ne la mia, ne la tua...
 )
)Leggendo che hai dei dubbi sulla formula, ti mando il file completo.
Link
La tua formula mi pare giusta. L'ho sottoposta a vari controlli e non fa una piega.
Inoltre, per quanto poco pratica, è una bella formula e, come diceva Hardy (cfr. "Apologia di un matematico"), la bellezza è ciò che più conta in matematica.
Ci sto lavorando sopra per vedere se riesco a cavarne fuori un'altra formula esplicita, magari più elegante di
Prob("nessuna coincidenza")=$\sum_{k=2}^N\frac{(-)^k}{k!}$
Se ottengo qualcosa, ti avverto.
Quanto al mio "atteggiamento permanente di sfida", devo dirti che nemmeno tu sei un tranquillo angioletto.
Non ti ho mai visto (come invece faccio io ogni tanto) esprimere apprezzamento per il lavoro altrui o sottolineare l'eleganza di qualche bel risultato trovato da altri. E quando uno esprime il proprio apprezzamento per il tuo lavoro, tu che fai? Butti lì una battuta ironica, se non sarcastica, che vuole dire
(a) perchè ti aspettavi di meno ? e
(b) non sei certo tu all'altezza di darmi un voto!
Non è così forse?
Ma a me questo tuo modo di essere mica mi dà fastidio. Anzi!
Quel che conta è che i tuoi contributi siano (quasi) sempre ben mirati, asciutti, originali, lucidi e taglienti.
Ora mi aspetto la tua battutina di rimando!
Inoltre, per quanto poco pratica, è una bella formula e, come diceva Hardy (cfr. "Apologia di un matematico"), la bellezza è ciò che più conta in matematica.
Ci sto lavorando sopra per vedere se riesco a cavarne fuori un'altra formula esplicita, magari più elegante di
Prob("nessuna coincidenza")=$\sum_{k=2}^N\frac{(-)^k}{k!}$
Se ottengo qualcosa, ti avverto.
Quanto al mio "atteggiamento permanente di sfida", devo dirti che nemmeno tu sei un tranquillo angioletto.
Non ti ho mai visto (come invece faccio io ogni tanto) esprimere apprezzamento per il lavoro altrui o sottolineare l'eleganza di qualche bel risultato trovato da altri. E quando uno esprime il proprio apprezzamento per il tuo lavoro, tu che fai? Butti lì una battuta ironica, se non sarcastica, che vuole dire
(a) perchè ti aspettavi di meno ? e
(b) non sei certo tu all'altezza di darmi un voto!
Non è così forse?
Ma a me questo tuo modo di essere mica mi dà fastidio. Anzi!
Quel che conta è che i tuoi contributi siano (quasi) sempre ben mirati, asciutti, originali, lucidi e taglienti.
Ora mi aspetto la tua battutina di rimando!
"seascoli":
Ora mi aspetto la tua battutina di rimando!
Nessuna battutina, anzi un ringraziamento, perchè se metto su un piatto della bilancia il "bella formula" e gli aggettivi usati ai miei contributi, e sull'altro la mia ironia, mi sembra che il piatto penda di piu' da un lato.
Peraltro mi ci ritrovo anche sull'ironia. Per me il forum è un momento di relax, e quindi prendendolo alla leggera non ho alcuna intenzione di mettere i voti a qualcuno, ne tantomeno sono interessato a riceverli.
Certo che, quando leggo un intervento che definisce "uno sfacelo" l'intervento di un precedente utente, e poi scrivi inesatezze, è ovvio che qualcosa debba pur dire (...quann ce vò, ce vò...).
Ora ripassiamo al quesito.
"seascoli":
Ci sto lavorando sopra per vedere se riesco a cavarne fuori un'altra formula esplicita, magari più elegante di ....
Bene.
Sappi che durante la "generazione" di questa formula (e proprio in virtu' dell'analisi di come si comportavano i numeri della serie), si è presentato davanti un metodo ancora piu' facile, che riduce di molto i calcoli, e che la rende piu semplice.
Avevo pero' già creato la tabellina, e l'immagine da mettere sul forum, pertanto mi son detto "metto questa, e poi vediamo se qualcun altro la vede". Se hai interesse a trovarla, provaci, se invece ti interessa la soluzione, puoi chiederla.
Ciao.






 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo