[Scienza delle Costruzioni] Quale vincolo togliere per rendere isostatica una struttura

Data la struttura in immagine una volta iperstatica, ho dubbi su come individuare il vincolo da togliere per poi risolvere mediante due sistemi con le equazioni di Muller Breslau. La parte reticolare sovrastante non la toccherei, andrei quindi a modificare uno dei due incastri in A o H. E' lecito sostituire ad uno dei due incastri una cerniera?
Risposte
.
ho provato a risolvere l'esercizio mettendo una cerniera in A, il valore dell'incognita mi viene bruttino, pari a 347/75 ql^2.
.
Nel sistema con i carichi, l'equazione del momento nel tratto BC è $-2qx^3/l+19/2ql^2+13/2 qlx$ ?
Nel sistema con i carichi ottengo: $ Ha=-25/2ql ; Va=5ql; Hh=3/2 ql; Mh=-3/2ql^2; Vh=3 ql $
Nel tratto AB il momento mi viene: $25/2 qlx- 3qx^2$
Nel tratto BC $−2qx3l+192ql2+132qlx$
Nel tratto HG $3/2 ql^2 - 3/2 qlx$
Nel sistema con solo l'incognita X=1 ottengo $ Ha= -1/(2l); Va= 0; Hh= 1/(2l); Vh=0, Mh=-1/2 $
I momenti mi vengono:
AB $ x/(2l) - 1 $
BC $ -1/2 + x/(2l) $
HG $ 1-x/(2l) $
Il momento effettivo in A mi viene $347/75 ql^2$
Nel tratto AB il momento mi viene: $25/2 qlx- 3qx^2$
Nel tratto BC $−2qx3l+192ql2+132qlx$
Nel tratto HG $3/2 ql^2 - 3/2 qlx$
Nel sistema con solo l'incognita X=1 ottengo $ Ha= -1/(2l); Va= 0; Hh= 1/(2l); Vh=0, Mh=-1/2 $
I momenti mi vengono:
AB $ x/(2l) - 1 $
BC $ -1/2 + x/(2l) $
HG $ 1-x/(2l) $
Il momento effettivo in A mi viene $347/75 ql^2$
.
Hg l'ho scritto bene nello schemettino che mi faccio per calcolare n,t,m dei vari tratti, , però poi nell'equazione ci ho scritto 1, e quindi sia il primo che il secondo integrale hanno un errore.
Nel sistema con i carichi, che a noi fanno chiamare $ S^0 $ ho messo $Ha$ e $Hh$ che puntano a destra, $Va$ e $Vh$ verso l'alto e $Mh$ antiorario. Nel secondo sistema considero l'incognita in $A$ $x=1$ sempre antiorario
Nel sistema con i carichi, che a noi fanno chiamare $ S^0 $ ho messo $Ha$ e $Hh$ che puntano a destra, $Va$ e $Vh$ verso l'alto e $Mh$ antiorario. Nel secondo sistema considero l'incognita in $A$ $x=1$ sempre antiorario
.
Questo è l'esploso

il sistema mi viene:
$ Ha+Hc=-6ql-3ql=-9ql; $
$ Va+Vc=0 $
momento orario rispetto ad A $ -6ql(1/2l)-3ql(1/3l+l)-2lHc
=0 $
$ Vg-Vc-6ql-2ql=0 $
$ Hc=Hg $
momento orario rispetto a C $ -6ql(l)-2ql(3l)+4lVg=0 $
$ Vh=Vg $
$ Hg=Hh+2ql $
momento orario rispetto a H $ Mh+lHg -2ql^2=0 $

il sistema mi viene:
$ Ha+Hc=-6ql-3ql=-9ql; $
$ Va+Vc=0 $
momento orario rispetto ad A $ -6ql(1/2l)-3ql(1/3l+l)-2lHc
=0 $
$ Vg-Vc-6ql-2ql=0 $
$ Hc=Hg $
momento orario rispetto a C $ -6ql(l)-2ql(3l)+4lVg=0 $
$ Vh=Vg $
$ Hg=Hh+2ql $
momento orario rispetto a H $ Mh+lHg -2ql^2=0 $
.
In quello che ho fatto io ho trovato un errore, nel sistema $S^0$ mi sono perso un segno nell'equazione del momento rispetto ad A e ho ottenuto Hc positivo anzichè negativo.
Non ho capito perchè la forza orizzontale 2ql va sulla reticolare e non sulla colonna, l'importante non è piazzarla una volta soltanto su uno dei due "lati" di G?
Se dici che va messa tassativamente sulla reticolare mi fido, però per non incappare più nell'errore vorrei capire il motivo perchè non lo so.
Non ho capito perchè la forza orizzontale 2ql va sulla reticolare e non sulla colonna, l'importante non è piazzarla una volta soltanto su uno dei due "lati" di G?
Se dici che va messa tassativamente sulla reticolare mi fido, però per non incappare più nell'errore vorrei capire il motivo perchè non lo so.
.
Ho rifatto i conti e X1 mi viene $13/5 ql^2$
Chiarissimo, grazie
"sellacollesella":
Ovviamente va capito il perché, altrimenti la volta in cui dico una cazzata la prendi per buona e ... ciao!
Partiamo da una punto fermo: la forza concentrata è applicata al nodo, quindi sul nodo rimane SEMPRE.
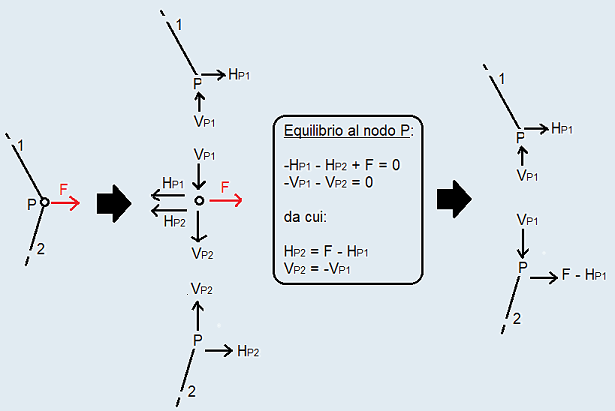
D'altro canto, solitamente si incappa in situazioni del seguente tipo:
\(\quad\quad\quad\)
dove si è soliti ignorare che, a rigore, occorrerebbe esplodere come mostrato nel mezzo, in quanto seppur puntiforme anche la cerniera \(P\) è un corpo che deve essere posto in equilibrio! Invece, quello che si fa inconsciamente è passare direttamente dalla parte sinistra alla parte destra dell'immagine. Il fatto che ciò funzioni porta a pensare che si faccia sempre così, mentre appena le cose si complicano cade il palco!
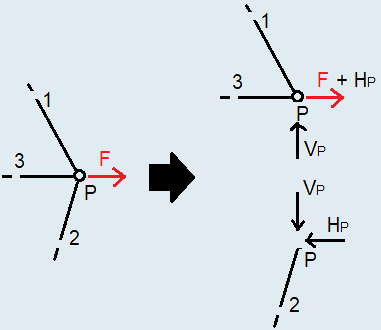
Pertanto, tornando alla situazione in cui siamo incappati nella struttura oggetto di studio, si ha:
\(\quad\quad\quad\quad\quad\quad\quad\quad\quad\)
dove, ancora una volta la forza applicata esternamente di intensità \(F\) la si deve applicare al nodo \(P\).
Dato che in questo caso il corpo superiore non lo abbiamo esploso, la forza \(F\) dovrà necessariamente essere riportata sulla cerniera \(P\) presente in tale corpo, nulla ha a che vedere la trave inferiore! Vedi se torna.
.
nel sistema $S^0$ : $Ha=-11/2 ql$ ; $Va=5ql$ ; $"Hc=-7/2 ql$ ; $Hg=3/2 ql$ ; $Vc=-5ql$ ; $Vg=3ql$ ; $Hh=3/2 ql$; $Vh= 3ql$ $Mh=-3/2ql^2$
in AB $ M=11/2qlx -3qx^2$
in BC $M=5/2ql^2+2qlx-2q(x^3)/l$
in HG $M=3/2ql^2-3/2qlx$
in AB $ M=11/2qlx -3qx^2$
in BC $M=5/2ql^2+2qlx-2q(x^3)/l$
in HG $M=3/2ql^2-3/2qlx$
.
Dovrei aver trovato l'errore, ho sbagliato a sostituire un Hc senza cambiare di segno, $Hh=-11/2 ql$ e $Hg=-11/2 ql$
.
$Mh=11/2ql^2$
Il momento flettente su BC viene $M=5/2ql^2-2q(x^3)/l-1/2qlx$ , in GH $M=11/2qlx-11/2 ql^2$
Il momento flettente su BC viene $M=5/2ql^2-2q(x^3)/l-1/2qlx$ , in GH $M=11/2qlx-11/2 ql^2$



 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo