Scienza delle costruzioni
Salve a tutti. sto risolvendo questa struttura isostatica
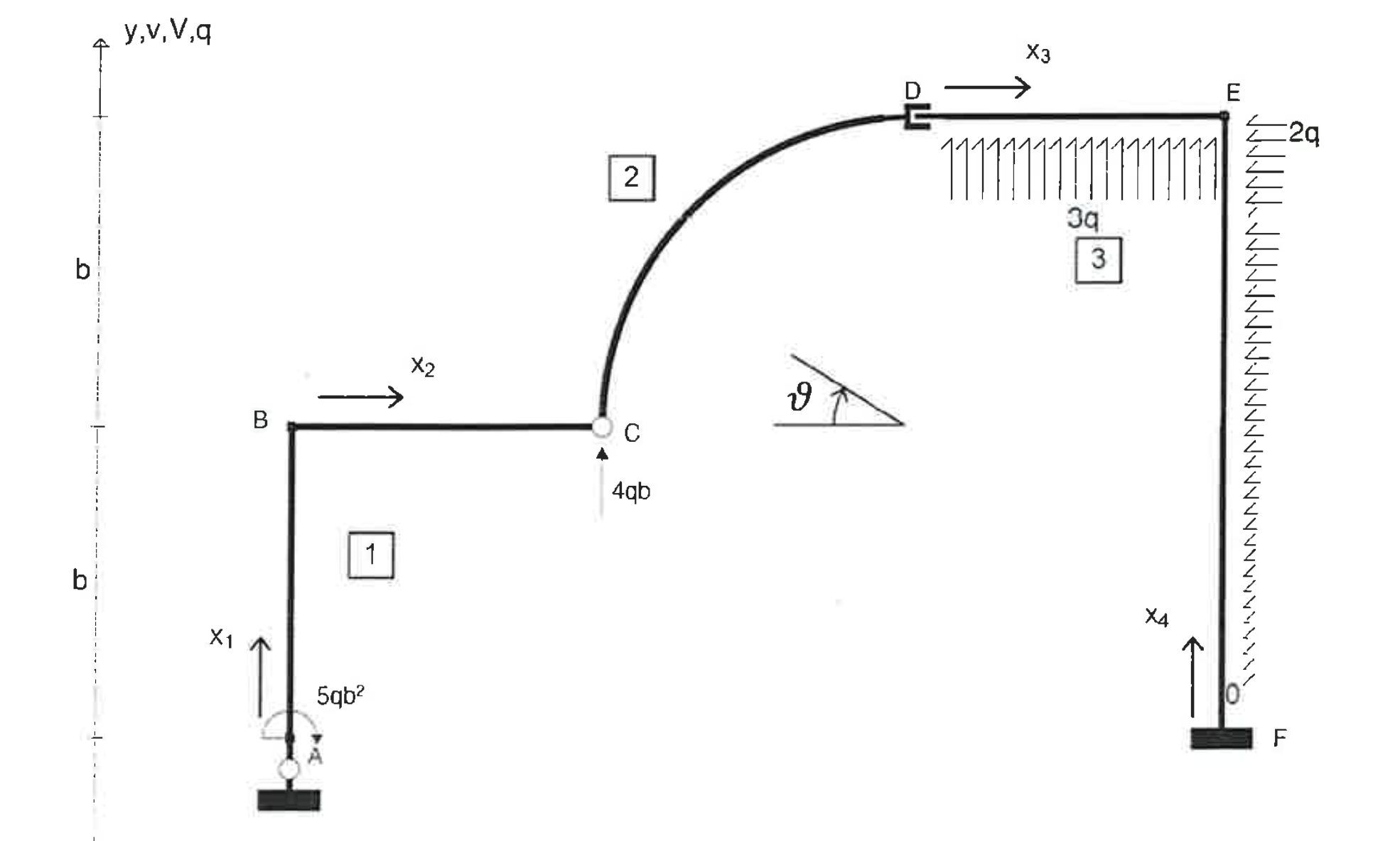
Le reazioni vincolari che ho calcolato sono:
xA=0
yA=5qb verso il basso
xF=2qb verso destra
yF=2qb verso il basso
MF 11/6 qb^2 oraria
I risultati coincidono tutti a meno del momento nell'incastro. L'ho rifatta anche provando con polii diversi ma rimane uguale. Qualcuno può aiutarmi?
Grazie

Le reazioni vincolari che ho calcolato sono:
xA=0
yA=5qb verso il basso
xF=2qb verso destra
yF=2qb verso il basso
MF 11/6 qb^2 oraria
I risultati coincidono tutti a meno del momento nell'incastro. L'ho rifatta anche provando con polii diversi ma rimane uguale. Qualcuno può aiutarmi?
Grazie
Risposte
In effetti mi risulta MF = 19/6 q b^2 in verso orario. Torna con quanto atteso?
Si il risultato è corretto 19/6qb^2 però allora non capisco dove sbaglio.Potresti farmi vedere la soluzione o il posizionamento delle forze? sono incerto sul carico triangolare. Ha modulo 2qb ed è posizionato ad 1/3b dal punto a maggiore intensità?
ok ho capito contavo il braccio come 2/3b e non 1+2/3b cioè 4/3b da A.
Si. Il carico triangolare è equivalente ad un carico concentrato pari a 2 q b e distante 4/3 b da F.
Grazie mille per l'aiuto!
In realtà un altro dubbio: studiando le forze interne nel tratto curvo posso semplificarmi la vita andando a calcolare il valore delle reazioni della cerniera "staccando" il tratto ABC. ho solo il valore della forza verticale yC= qb. Il dubbio è: il valore della forza 4qb sulla cerniera è da contare quando calcolo le azioni interne? oppure è già conteggiata nel valore della reazione della cerniera?
Normalmente, in assenza di forze dirette su un vincolo tra 2 travi, l'equilibrio del vincolo stesso impone che le reazioni su una trave siano uguali ed opposte a quelle sull'altra trave e quindi imponendo tale condizione a priori si può ignorare l'equazione di equilibrio del vincolo.
Nel caso di forze dirette sul vincolo questa assunzione non è più vera e bisogna considerare che il vincolo imporrà delle reazioni vincolari diverse sulle 2 travi, che saranno legate tra loro dall'equilibrio del vincolo soggetto alle reazioni delle due travi e dalla forza applicata direttamente.
In questo caso, oltre alla trave ABC e alla trave CD, si deve considerare separatamente anche l'equilibrio della cerniera C a cui va applicata la forza 4qb.
Nel caso di forze dirette sul vincolo questa assunzione non è più vera e bisogna considerare che il vincolo imporrà delle reazioni vincolari diverse sulle 2 travi, che saranno legate tra loro dall'equilibrio del vincolo soggetto alle reazioni delle due travi e dalla forza applicata direttamente.
In questo caso, oltre alla trave ABC e alla trave CD, si deve considerare separatamente anche l'equilibrio della cerniera C a cui va applicata la forza 4qb.
Perfetto grazie ancora!
Ora, stessa struttura differenti carichi
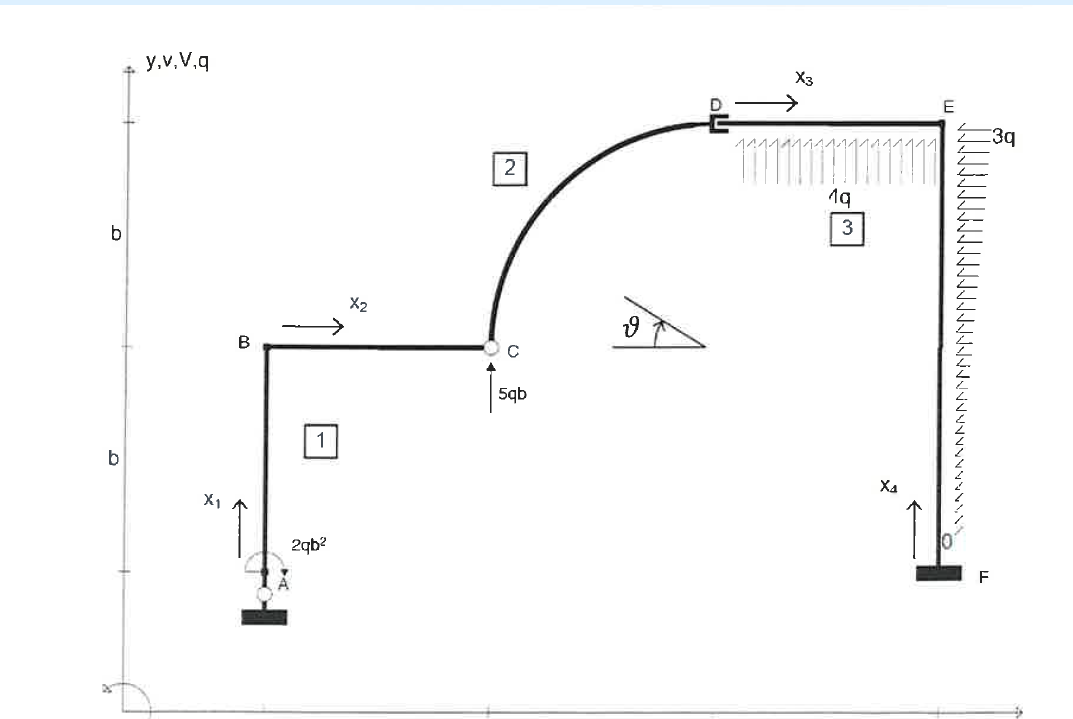
In questo caso mi viene:
xA=0
xF=3qb verso destra
yA=2qb verso il basso
yF=4qb verso il basso
MF=5/2qb^2 antiorario
Il testo mi dà come soluzione yF=7qb verso il basso e MF 4qb^2 antiorario.
Ora, stessa struttura differenti carichi

In questo caso mi viene:
xA=0
xF=3qb verso destra
yA=2qb verso il basso
yF=4qb verso il basso
MF=5/2qb^2 antiorario
Il testo mi dà come soluzione yF=7qb verso il basso e MF 4qb^2 antiorario.
Senza esplodere la struttura e ricalcolare tutte le reazioni, ma assumendo corrette le reazioni in A, si ha (per l'asse y verso positivo diretto verso l'alto mentre per i momenti verso positivo antiorario e polo in F):
yF = -(5qb + 4qb + yA) = -(5qb + 4qb - 2qb) = -7qb ovvero 7qb verso il basso
MF = -(3qb*4/3b-4qb*b/2-5qb*2b-2qb^2+yA*3b ) = -(4qb^2-2qb^2-10qb^2 -2qb^2+2qb*3b ) = 4qb^2 verso antiorario
Quindi i risultati del testo direi che sono corretti.
yF = -(5qb + 4qb + yA) = -(5qb + 4qb - 2qb) = -7qb ovvero 7qb verso il basso
MF = -(3qb*4/3b-4qb*b/2-5qb*2b-2qb^2+yA*3b ) = -(4qb^2-2qb^2-10qb^2 -2qb^2+2qb*3b ) = 4qb^2 verso antiorario
Quindi i risultati del testo direi che sono corretti.
A me sembrava un 1 non un 4 qb forse sbaglio per questo.
Grazie mille
Grazie mille
Ora per le azioni interne ho un dubbio:
Nel tratto CD (quello curvo) prendo come ascissa l'angolo theta. Per evitare di "portarmi dietro" il tratto AB decido di calcolare il valore delle reazioni vincolari in C.
Se considero ABC e la forza 5qb mi viene yC=3qb verso il basso.
Se considero CDEF senza la forza 5qb,(la forza 5qb la devo ricontare?) mi viene yC=3qb verso l'alto.
Per le forze interne devo tenere conto di quest'ultima visto che il tratto considerato è CD giusto?
In generale come dovrei procedere per queso tipo di situazioni?
Grazie.
Nel tratto CD (quello curvo) prendo come ascissa l'angolo theta. Per evitare di "portarmi dietro" il tratto AB decido di calcolare il valore delle reazioni vincolari in C.
Se considero ABC e la forza 5qb mi viene yC=3qb verso il basso.
Se considero CDEF senza la forza 5qb,(la forza 5qb la devo ricontare?) mi viene yC=3qb verso l'alto.
Per le forze interne devo tenere conto di quest'ultima visto che il tratto considerato è CD giusto?
In generale come dovrei procedere per queso tipo di situazioni?
Grazie.
L'equilibrio della trave ABC richiede che la forza interna dovuta al vincolo sia
yC(ABC) = -yA = 2qb diretta verso l'alto
mentre l'equilibrio delle travi CDEF richiede che sia
yC(CDEF) = -yF - 4qb = 7qb - 4qb = 3qb diretta verso l'alto
Sul vincolo C avremo le reazioni dovute alle travi e la forza 5qb, per cui
-yC(ABC) -yC(CDEF) + 5qb = -2qb - 3qb + 5qb = 0
come è corretto che sia.
A questo punto dovrebbe essere abbastanza chiaro cosa considerare su ogni tratto.
yC(ABC) = -yA = 2qb diretta verso l'alto
mentre l'equilibrio delle travi CDEF richiede che sia
yC(CDEF) = -yF - 4qb = 7qb - 4qb = 3qb diretta verso l'alto
Sul vincolo C avremo le reazioni dovute alle travi e la forza 5qb, per cui
-yC(ABC) -yC(CDEF) + 5qb = -2qb - 3qb + 5qb = 0
come è corretto che sia.
A questo punto dovrebbe essere abbastanza chiaro cosa considerare su ogni tratto.
Ah ok credo dia ver capito! Grazie davvero :)


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo