Spira in campo magnetico
Salve a tutti, sto cercando di risolvere questo esercizio:
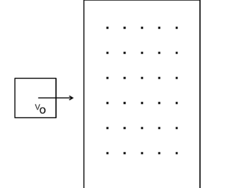
Una spira quadrata di lato $a$ viene inserita in una regione di spazio in cui è presente un campo magnetico (perpendicolare alla superfice della spira) variabile nel tempo. La spira si muove con velocità costante $v_0$ e si osserva che ai capi della stessa si instaura una forza elettromotrice pari a:
$fem = K(1-\frac{t}{\tau})e^(- \frac{t}{\tau})$
Con K e $\tau$ costanti positive.
Tale relazione è da ritenersi valida fino ad un attimo prima che la spira risulti totalmente immersa nella regione in cui è presente il campo.
Dimostra che se $v < \frac{a}{\tau}$ allora si osserva, mentre il circuito viene immerso nella regione con il campo, una inversione del senso di circolazione della corrente.
Ora, io so che la corrente indotta cambia verso di circolazione se la fem indotta cambia segno.
Dall'espressione della fem data, essa cambia segno a seconda che $(1-\frac{t}{\tau})$ sia positivo o negativo. Quindi per $0 \leq t< \tau$ la fem è positiva e $t>\tau$ è negativa.
So che il moto della spira è rettilineo uniforme, quindi potrei esprimere la superfice di spira immersa nella regione del campo al generico tempo $t$ come $v_0ta$, con la precedente.
non so, leggendola, la traccia non è al 100% chiara.
EDIT
rileggendo la traccia piu' volte, l'ho interpretata cosi' "dimostra che se la velocità (costante) con cui si muove la spira è minore di $\frac{a}{\tau}$ allora effettivamente la fem cambia di segno prima che la spira entri completamente nella regione del campo" (perchè da quel momento l'espressione della fem data non risulta piu' valida).
Quindi ponendo come istante iniziale il momento immediatamente precedente a quello in cui il lato anteriore entra nella zona del campo:

E quindi alla fine è come dimostrare che se la spira si muove con una velocità minore di $\frac{a}{\tau}$, la spira non riesce ad entrare tutta prima che sia trascorso un tempo pari a $\tau$.
Essendo un moto rettilineo uniforme, questo equivale a chiedersi il tempo che la spira impiega per percorrere una distanza pari ad $a$, quindi $t=\frac{a}{v_0}$ voglio che tale tempo sia maggiore di quello necessario alla fem per cambiare segno.
Quindi
$\frac{a}{v_0} > \tau$ da cui $v < \frac{a}{\tau}$
Però continuo ad avere la sensazione che la traccia sia poco chiara, un po' "ambigua"

Una spira quadrata di lato $a$ viene inserita in una regione di spazio in cui è presente un campo magnetico (perpendicolare alla superfice della spira) variabile nel tempo. La spira si muove con velocità costante $v_0$ e si osserva che ai capi della stessa si instaura una forza elettromotrice pari a:
$fem = K(1-\frac{t}{\tau})e^(- \frac{t}{\tau})$
Con K e $\tau$ costanti positive.
Tale relazione è da ritenersi valida fino ad un attimo prima che la spira risulti totalmente immersa nella regione in cui è presente il campo.
Dimostra che se $v < \frac{a}{\tau}$ allora si osserva, mentre il circuito viene immerso nella regione con il campo, una inversione del senso di circolazione della corrente.
Ora, io so che la corrente indotta cambia verso di circolazione se la fem indotta cambia segno.
Dall'espressione della fem data, essa cambia segno a seconda che $(1-\frac{t}{\tau})$ sia positivo o negativo. Quindi per $0 \leq t< \tau$ la fem è positiva e $t>\tau$ è negativa.
So che il moto della spira è rettilineo uniforme, quindi potrei esprimere la superfice di spira immersa nella regione del campo al generico tempo $t$ come $v_0ta$, con la precedente.
non so, leggendola, la traccia non è al 100% chiara.
EDIT
rileggendo la traccia piu' volte, l'ho interpretata cosi' "dimostra che se la velocità (costante) con cui si muove la spira è minore di $\frac{a}{\tau}$ allora effettivamente la fem cambia di segno prima che la spira entri completamente nella regione del campo" (perchè da quel momento l'espressione della fem data non risulta piu' valida).
Quindi ponendo come istante iniziale il momento immediatamente precedente a quello in cui il lato anteriore entra nella zona del campo:

E quindi alla fine è come dimostrare che se la spira si muove con una velocità minore di $\frac{a}{\tau}$, la spira non riesce ad entrare tutta prima che sia trascorso un tempo pari a $\tau$.
Essendo un moto rettilineo uniforme, questo equivale a chiedersi il tempo che la spira impiega per percorrere una distanza pari ad $a$, quindi $t=\frac{a}{v_0}$ voglio che tale tempo sia maggiore di quello necessario alla fem per cambiare segno.
Quindi
$\frac{a}{v_0} > \tau$ da cui $v < \frac{a}{\tau}$
Però continuo ad avere la sensazione che la traccia sia poco chiara, un po' "ambigua"
Risposte
Osservando che:
si ha:
Quindi, poiché il sistema sottostante:
deve ammettere soluzione, necessariamente:
$t=x/v$
si ha:
$fem=K(1-x/(v\tau))e^(-t/\tau)$
Quindi, poiché il sistema sottostante:
$\{(x lt a),(1-x/(v\tau) lt 0):} rarr \{(x lt a),(x gt v\tau):}$
deve ammettere soluzione, necessariamente:
$v\tau lt a$
"anonymous_0b37e9":
Osservando che:
$t=x/v$
si ha:
$fem=K(1-x/(v\tau))e^(-t/\tau)$
Quindi, poiché il sistema sottostante:
$\{(x lt a),(1-x/(v\tau) lt 0):} rarr \{(x lt a),(x gt v\tau):}$
deve ammettere soluzione, necessariamente:
$v\tau lt a$
Ok quindi l'interpretazione che ne ho dato nel precedente post era corretta, ti ringrazio
"PietroGMC":
... se la spira si muove con una velocità minore di $a/\tau$, la spira non riesce ad entrare tutta prima che sia trascorso un tempo pari a $\tau$ ...
Non mi sembra questo il punto. Piuttosto, se la velocità è troppo elevata, la fem non cambia segno prima che la spira sia entrata completamente.
"anonymous_0b37e9":
[quote="PietroGMC"]
... se la spira si muove con una velocità minore di $a/\tau$, la spira non riesce ad entrare tutta prima che sia trascorso un tempo pari a $\tau$ ...
Non mi sembra questo il punto. Piuttosto, se la velocità è troppo elevata, la fem non cambia segno prima che la spira sia entrata completamente.[/quote]
non è la stessa cosa?
Dire "Se la velocità è troppo elevata la fem non cambia segno prima che la spira sia entrata tutta",
non è come dire che "se la velocità è bassa (quindi minore di $a/\tau$) la spira non riesce ad entrare completamente prima che sia trascorso un tempo pari a $\tau$ (che è il tempo dopo il quale la fem cambia segno)?"
Hai ragione, è la stessa cosa.
@ PietroGMC
E se il testo avesse richiesto anche la fem indotta con spira completamente immersa, come avresti risposto?
E se il testo avesse richiesto anche la fem indotta con spira completamente immersa, come avresti risposto?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo