Massa-molla-smorzatore
Ho il seguente sistema
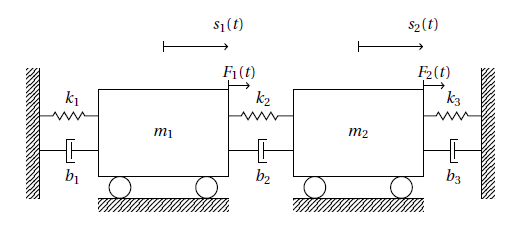
il mio testo assume queste direzioni per le forze
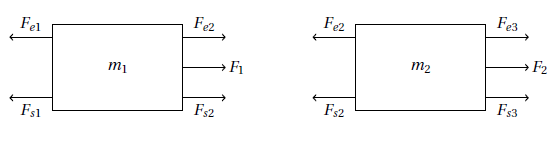
Io però penso che:
- $F_{e2}$ e $F_{s2}$ agiscono in verso opposto* su $m_1$
- $F_{e2}$ e $F_{s2}$ agiscono in verso opposto* su $m_2$
- $F_{e3}$ e $F_{s3}$ hanno verso opposto* siccome la molla è in contrazione
*rispetto alla seconda immagine
Sapete dirmi qual è la soluzione corretta?

il mio testo assume queste direzioni per le forze
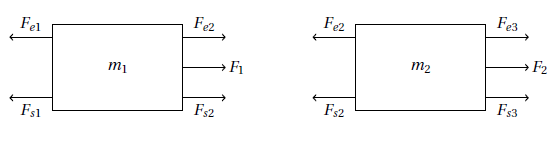
Io però penso che:
- $F_{e2}$ e $F_{s2}$ agiscono in verso opposto* su $m_1$
- $F_{e2}$ e $F_{s2}$ agiscono in verso opposto* su $m_2$
- $F_{e3}$ e $F_{s3}$ hanno verso opposto* siccome la molla è in contrazione
*rispetto alla seconda immagine
Sapete dirmi qual è la soluzione corretta?
Risposte
E' una questione di convenzioni.
Per come le mette lui nel disegno, devi stare attento ai segni.
Per esemio $F_(e3)=-k_3s_2$.
Se le rappresentassi come dici tu, ovviamente sarebbe $F_(e3)=k_3s_2$
L'importante e' che, una volta rappresentate le forze, ti ricordi che la forza si opponga allo spostamento
Per come le mette lui nel disegno, devi stare attento ai segni.
Per esemio $F_(e3)=-k_3s_2$.
Se le rappresentassi come dici tu, ovviamente sarebbe $F_(e3)=k_3s_2$
L'importante e' che, una volta rappresentate le forze, ti ricordi che la forza si opponga allo spostamento
$F_{e1}=k_1s_1$
$F_{e2}=k_2(s_2-s_1)$
$F_{e3}=k_3s_3$
$F_{s1}=b_1\dot{s}_1$
$F_{s2}=b_2(\dot{s}_2-\dot{s}_1)$
$F_{s3}=b_3\dot{s}_3$
E mi trovo che:
$m\ddot{s_1}=F_1-F_{e1}-F_{s1}-F_{e2}-F_{s2}$
$m\ddot{s_2}=F_2+F_{e2}+F_{s2}-F_{e3}-F_{s3}$
$F_{e2}=k_2(s_2-s_1)$
$F_{e3}=k_3s_3$
$F_{s1}=b_1\dot{s}_1$
$F_{s2}=b_2(\dot{s}_2-\dot{s}_1)$
$F_{s3}=b_3\dot{s}_3$
E mi trovo che:
$m\ddot{s_1}=F_1-F_{e1}-F_{s1}-F_{e2}-F_{s2}$
$m\ddot{s_2}=F_2+F_{e2}+F_{s2}-F_{e3}-F_{s3}$
Stai scrivendo usando il disegno in figura, o ti sei scelto un sistema tuo (non mi va di controllare) 

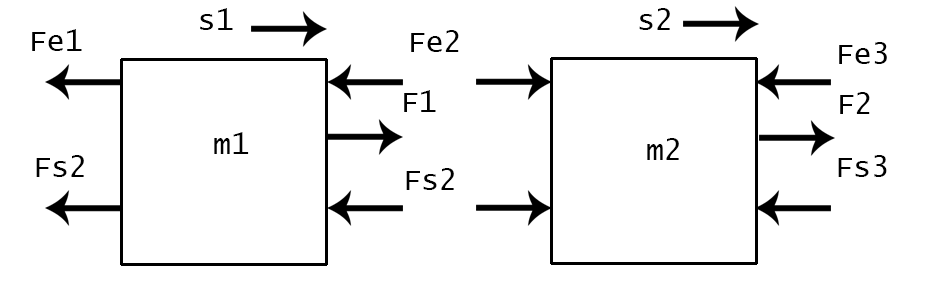
Fe1 va bene, Fe2 no. Se la s2 e s1 aumenta (e' positivo), la molla si sta allungando. Quindi le forze sono opposte a quelle che disegni tu, pertanto ci vuole un segno meno davanti alla parentesi.
"professorkappa":
Fe1 va bene, Fe2 no. Se la s2 e s1 aumenta (e' positivo), la molla si sta allungando. Quindi le forze sono opposte a quelle che disegni tu, pertanto ci vuole un segno meno davanti alla parentesi.
Vorrei ritornare un attimo sul problema.
Se la molla 1 e la molla 2 sono entrambe allungate, la molla 3 non dovrebbe essere in compressione?
E poi, la molla 2 indipendentemente dagli ordini di grandezza per s2 ed s1, si allunga sempre? Se s1>s2 non dovrebbe essere in compressione?
Si, infatti. Tu assumi dei versi positivi, i calcoli poi ti dicono se son quelli giusti,e ti descrivono se le molle si allungano o si accorciano. Importa poco come scegli, l'importante e' la coerenza nello scrivere i segni delle equazioni.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo