Due dubbi su pendoli semplici e composti
Ciao di nuovo 
Credo di avere un dubbio sul pendolo composto. E' inerente a: $M=-F_pdsintheta$ ovviamente si vede bene che il segno a dx deve essere meno, con la regola della mano destra e spostando ad esempio in senso antiorario il corpo (alzandolo cioè a destra) entra nel pinao del foglio il vettore M, quindi meno.
Veniamo al dubbio, io so che $(dL)/(dt)=M$ per il thm del momento angolare. Ora, dL/dt deve essere concorde in segno a M, però se calcolo dL mi sembra uscente e non concorde ad M, questo perché L(t+dt) ha valore maggiore di L(t) nel momento in cui lascio andare l'oggetto.
Non capisco l'errore.
Credo di avere un dubbio sul pendolo composto. E' inerente a: $M=-F_pdsintheta$ ovviamente si vede bene che il segno a dx deve essere meno, con la regola della mano destra e spostando ad esempio in senso antiorario il corpo (alzandolo cioè a destra) entra nel pinao del foglio il vettore M, quindi meno.
Veniamo al dubbio, io so che $(dL)/(dt)=M$ per il thm del momento angolare. Ora, dL/dt deve essere concorde in segno a M, però se calcolo dL mi sembra uscente e non concorde ad M, questo perché L(t+dt) ha valore maggiore di L(t) nel momento in cui lascio andare l'oggetto.
Non capisco l'errore.
Risposte
Non ho mica capito che vuoi dire.
La derivata del momento angolare è concorde col momento della forza peso ovviamente: se supponi un angolo positivo il momento della forze peso è negativo e la variazione del momento angolare rispetto al tempo sarà pure negativa.
La derivata del momento angolare è concorde col momento della forza peso ovviamente: se supponi un angolo positivo il momento della forze peso è negativo e la variazione del momento angolare rispetto al tempo sarà pure negativa.
Esatto i segni dovrebbero essere concordi, però se analizzo l'oggetto in moto di discesa e che ha angolo positivo che si riduce a me sembra che M abbia segno negativo, ma quando scrivo dL mi pare positivo, infatti al tempo L(t+dt) il valore è maggiore di L(t) in valore assoluto (questo perché in t+dt più velocità) quindi sottraendoli dovrei avere segno positivo essendo L entrante. Sottraggo quindi L(t+dt) che et qualcosa di negativo a L(t) anch'esso negativo ma di valore assoluto minore, quindi dL>0
PS: vorrei poi aggiungere una domanda sul pendolo semplice, ma facciamo una cosa per volta
PS: vorrei poi aggiungere una domanda sul pendolo semplice, ma facciamo una cosa per volta
"alticco":
....[....] Sottraggo quindi L(t+dt) che è qualcosa di negativo a L(t) anch'esso negativo ma di valore assoluto minore, quindi dL>0
Veramente per definizione $(dL)/dt=(L(t+dt)-L(t))/dt$ (sperando che i matematici qui ci perdonino per la notazione non rigorosa), quindi nel tuo esempio ottieni di certo qualcosa di negativo visto che $L(t+dt)<0$, $L(t)<0$ ma $|L(t+dt)|>|L(t)|$
@Faussone
Dovresti mettere , al secondo membro, dei $Deltat$ anziché $dt$ , e scrivere il passaggio al limite del rapporto incrementale per $Deltatrarr0$ , e così la definizione di derivata è giusta. Sorry.
Dovresti mettere , al secondo membro, dei $Deltat$ anziché $dt$ , e scrivere il passaggio al limite del rapporto incrementale per $Deltatrarr0$ , e così la definizione di derivata è giusta. Sorry.
Hai ragione, mi sono ingarbugliato un sacco, perdonatemi. Grazie mille per il chiarimento.
Volevo gentilmente porre un secondo dubbio, però sul pendolo semplice come anticipavo: mi rendo conto che essendo il moto del pendolo semplice di tipo circolare, allora nel SDR laboratorio lungo la direzione radiale della corda che sostiene l'oggetto ho sia l'azione della forza di gravità (scomposta in tal direzione) che la forza centripeta. La tensione della corda avrà quindi valore opposto della forza di gravità sommataal valore della forza centripeta (ho infatti una accelerazione centripeta che tiene l'oggetto in moto circolare).
Ora viene il dubbio, quando mi sposto in un SDR solidale con l'oggetto in moto, poiché l'oggetto è per me fermo (in tal sdr) quando il professore scompone la forza di gravità lungo la direzione radiale e la tensione della corda le ritengo uguali e contrarie e qundi ho accelerazione nulla agente sull'oggetto appeso. Ecco, però non mi torna qualcosa: cosa compensa la forza centripeta prima esistente? Non considero nessuna forza apparente in questo sistema non inerziale. Non riesco bene a capire.
Volevo gentilmente porre un secondo dubbio, però sul pendolo semplice come anticipavo: mi rendo conto che essendo il moto del pendolo semplice di tipo circolare, allora nel SDR laboratorio lungo la direzione radiale della corda che sostiene l'oggetto ho sia l'azione della forza di gravità (scomposta in tal direzione) che la forza centripeta. La tensione della corda avrà quindi valore opposto della forza di gravità sommataal valore della forza centripeta (ho infatti una accelerazione centripeta che tiene l'oggetto in moto circolare).
Ora viene il dubbio, quando mi sposto in un SDR solidale con l'oggetto in moto, poiché l'oggetto è per me fermo (in tal sdr) quando il professore scompone la forza di gravità lungo la direzione radiale e la tensione della corda le ritengo uguali e contrarie e qundi ho accelerazione nulla agente sull'oggetto appeso. Ecco, però non mi torna qualcosa: cosa compensa la forza centripeta prima esistente? Non considero nessuna forza apparente in questo sistema non inerziale. Non riesco bene a capire.
Ahi ahi ahi!
Fai una enorme confusione, stai attento!
La forza centripeta è presente nel sistema di riferimento inerziale quindi NON è una forza apparente, come lo è la forza centrifuga.
Quindi la forza centripeta (che significa letteralmente forza verso il centro) è, a secondo del caso che consideri, una certa precisa forza.
Per un satellite che ruota attorno alla Terra (supponiamo in moto circolare uniforme tanto per non complicare le cose) la forza centripeta è la forza di attrazione gravitazionale che permette al satellite proprio di percorrere l'orbita circolare, altrimenti il satellite procederebbe di moto rettilineo uniforme; per una macchina che percorre una curva in piano la forza centripeta è la forza di attrito delle ruote, altrimenti la macchina andrebbe dritta...; per il pendolo semplice in oggetto la forza centripeta è la tensione del filo.
Fai una enorme confusione, stai attento!
La forza centripeta è presente nel sistema di riferimento inerziale quindi NON è una forza apparente, come lo è la forza centrifuga.
Quindi la forza centripeta (che significa letteralmente forza verso il centro) è, a secondo del caso che consideri, una certa precisa forza.
Per un satellite che ruota attorno alla Terra (supponiamo in moto circolare uniforme tanto per non complicare le cose) la forza centripeta è la forza di attrazione gravitazionale che permette al satellite proprio di percorrere l'orbita circolare, altrimenti il satellite procederebbe di moto rettilineo uniforme; per una macchina che percorre una curva in piano la forza centripeta è la forza di attrito delle ruote, altrimenti la macchina andrebbe dritta...; per il pendolo semplice in oggetto la forza centripeta è la tensione del filo.
Sì certo, quello che dici mi torna. Perdonami se mi sono espresso male spero di poter rimendiare.
Quello che volevo dire è che nel sdr inerziale O (laboratorio ad es.) ho la forza centripeta per tenere il moto circolare, poi ho la forza peso e la tensione. La tensione è in modulo pari alla somma della forza peso scomposta più la forza centripeta (è ilfilo con la tensione a tenere il moto circolare del corpo).
Poi, io so che ogni volta che ho una forza centripeta passando in un sdr non inerziale ho una forza apparente (la centrifuga ad es). Se prendo infatti come origine del sistema non inerziale O' il fulcro dove è appeso il pendolo, allora vedo che l'oggetto è fermo poiché ho una forza centrifuga e una parte della tensione che si oppone. C'è poi sempre il contributo della forza di gravità scomposta lungo la corda che rientra nella tensione.
Il sdr dubbio è quello dell'oggetto in moto O'': immaginando di sedermi sull'oggetto che "pendola" il professore considera solo due forze: forza peso e tensione che la bilancia e dice che a=0 dell'oggetto in questo sistema di riferimento. E a me questo non torna molto, perché mi sembra mancare una forza apparente che di solito nei non inerziali c'è: cioè considera solo forza peso e tensione, eppure proprio perché il moto è circolare nel sdr O allora in O'' dovrei anche avere una forza apparente. Qui sbaglio perché il prof non la considera proprio.
spero di poter rimendiare.Quello che volevo dire è che nel sdr inerziale O (laboratorio ad es.) ho la forza centripeta per tenere il moto circolare, poi ho la forza peso e la tensione. La tensione è in modulo pari alla somma della forza peso scomposta più la forza centripeta (è ilfilo con la tensione a tenere il moto circolare del corpo).
Poi, io so che ogni volta che ho una forza centripeta passando in un sdr non inerziale ho una forza apparente (la centrifuga ad es). Se prendo infatti come origine del sistema non inerziale O' il fulcro dove è appeso il pendolo, allora vedo che l'oggetto è fermo poiché ho una forza centrifuga e una parte della tensione che si oppone. C'è poi sempre il contributo della forza di gravità scomposta lungo la corda che rientra nella tensione.
Il sdr dubbio è quello dell'oggetto in moto O'': immaginando di sedermi sull'oggetto che "pendola" il professore considera solo due forze: forza peso e tensione che la bilancia e dice che a=0 dell'oggetto in questo sistema di riferimento. E a me questo non torna molto, perché mi sembra mancare una forza apparente che di solito nei non inerziali c'è: cioè considera solo forza peso e tensione, eppure proprio perché il moto è circolare nel sdr O allora in O'' dovrei anche avere una forza apparente. Qui sbaglio perché il prof non la considera proprio.
"alticco":
Quello che volevo dire è che nel sdr inerziale O (laboratorio ad es.) ho la forza centripeta per tenere il moto circolare, poi ho la forza peso e la tensione. La tensione è in modulo pari alla somma della forza peso scomposta più la forza centripeta (è il filo con la tensione a tenere il moto circolare del corpo).
Questo è sbagliato detto così (mi riferisco alla tua frase tra parentesi). La frase corretta è: la tensione è la forza centripeta che, sommata alla forza peso, tiene il corpo sulla traiettoria circolare. Nel caso specifico infatti sono le due forze che sommate tengono il corpo sulla traiettoria circolare.
"alticco":
Il sdr dubbio è quello dell'oggetto in moto O'': immaginando di sedermi sull'oggetto che "pendola" il professore considera solo due forze: forza peso e tensione che la bilancia e dice che a=0 dell'oggetto in questo sistema di riferimento. E a me questo non torna molto, perché mi sembra mancare una forza apparente che di solito nei non inerziali c'è: cioè considera solo forza peso e tensione, eppure proprio perché il moto è circolare nel sdr O allora in O'' dovrei anche avere una forza apparente. Qui sbaglio perché il prof non la considera proprio.
Se fa come dici sbaglia il professore, ma forse hai frainteso qualcosa.
Se sei in un sistema non inerziale vanno considerate oltre alle forze cosiddette "reali"[nota]Dico "reali" per capirci, ma a me non piace chiamarle reali perché anche le forze apparenti hanno un effetto reale, ma lasciamo perdere per ora questo discorso.[/nota], anche le forze apparenti, e nel tuo esempio la forza apparente è la forza centrifuga, quindi lungo il filo si ha forza centrifuga e componente del peso bilanciate dalla tensione. Questo nella direzione del filo, in direzione tangenziale invece, può esserci, se il pendolo sta accelerando nel riferimento assoluto, anche la forza di inerzia tangenziale, bilanciata dalla componente tangenziale del peso (ovvio che sulla verticale non c'è componente tangenziale del peso e in effetti l'accelerazione del pendolo nel sistema assoluto è nulla sulla verticale).
@faussone:
Grazie per la tua correzione, spero avrai ancora voglia di aiutarmi
Però non capisco: la tensione non è tutta forza centrifuga, è solo una parte di essa, perché una parte della tensione bilancia anche la forza peso. Quindi perché è sbagliato dire "una parte della tensione è la forza centripeta, infatti la tensione totale sommata vettorialemente alla forza peso danno come risultante la forza centripeta"?
"la tensione è la forza centripeta che" mi sembra quasi dire che la tensione è "=" forza centripeta, ma la tensione non finisce tutta in centripeta.
***********
Dico "professore" solo come abbreviazione per intendere quello che ho capito io ovviamente (lo dico per chiarezza da qui in poi), perché è altamente probabile (direi 99,9999999% che non abbia sbagliato nulla ma il tonto sia io
). Uso metodo del professore per comodità.
Quello che dici riesco a vederlo bene ponendomi nel chiodo che tiene il peso che oscilla: ho la forza peso che si elide con una parte della forza "tensione del filo", però una parte della tensione del filo rimane ed èquella che si elide con la forza apparente (centrifuga); sommando il tutto ho accelerazione nulla e infatti dal chiodo vedo sempre la pallina in fondo al filo ferma. Questo spero di averlo azzeccato
Però se mi sposto sul peso con la mia origine e il sdr quindi si muove assieme all'oggetto ecco... qui non riesco a vedere dove sia l'apparente (centrifuga). La vedo forse applicata al chiodo e che genera una parte di tensione?
Perché qui scrive https://www.matematicamente.it/appunti/ ... -semplice/
e non mi sembra consideri alcuna apparente. SOlo peso e tensione che si elidono.
Spero mi aiuterai a capire, perché vorrei proprio riuscirci.
Un immenso grazie per il tuo aiuto!
Grazie per la tua correzione, spero avrai ancora voglia di aiutarmi
"Faussone":
Questo è sbagliato detto così (mi riferisco alla tua frase tra parentesi). La frase corretta è: la tensione è la forza centripeta che, sommata alla forza peso, tiene il corpo sulla traiettoria circolare. Nel caso specifico infatti sono le due forze che sommate tengono il corpo sulla traiettoria circolare.
Però non capisco: la tensione non è tutta forza centrifuga, è solo una parte di essa, perché una parte della tensione bilancia anche la forza peso. Quindi perché è sbagliato dire "una parte della tensione è la forza centripeta, infatti la tensione totale sommata vettorialemente alla forza peso danno come risultante la forza centripeta"?
"la tensione è la forza centripeta che" mi sembra quasi dire che la tensione è "=" forza centripeta, ma la tensione non finisce tutta in centripeta.
***********
Dico "professore" solo come abbreviazione per intendere quello che ho capito io ovviamente (lo dico per chiarezza da qui in poi), perché è altamente probabile (direi 99,9999999% che non abbia sbagliato nulla ma il tonto sia io
). Uso metodo del professore per comodità."alticco":
Se fa come dici sbaglia il professore, ma forse hai frainteso qualcosa.
Se sei in un sistema non inerziale vanno considerate oltre alle forze cosiddette "reali", anche le forze apparenti, e nel tuo esempio la forza apparente è la forza centrifuga, quindi lungo il filo si ha forza centrifuga e componente del peso bilanciate dalla tensione. Questo nella direzione del filo, in direzione tangenziale invece, può esserci, se il pendolo sta accelerando nel riferimento assoluto, anche la forza di inerzia tangenziale, bilanciata dalla componente tangenziale del peso (ovvio che sulla verticale non c'è componente tangenziale del peso e in effetti l'accelerazione del pendolo nel sistema assoluto è nulla sulla verticale).
Quello che dici riesco a vederlo bene ponendomi nel chiodo che tiene il peso che oscilla: ho la forza peso che si elide con una parte della forza "tensione del filo", però una parte della tensione del filo rimane ed èquella che si elide con la forza apparente (centrifuga); sommando il tutto ho accelerazione nulla e infatti dal chiodo vedo sempre la pallina in fondo al filo ferma. Questo spero di averlo azzeccato
Però se mi sposto sul peso con la mia origine e il sdr quindi si muove assieme all'oggetto ecco... qui non riesco a vedere dove sia l'apparente (centrifuga). La vedo forse applicata al chiodo e che genera una parte di tensione?
Perché qui scrive https://www.matematicamente.it/appunti/ ... -semplice/
Scomponiamo la forza-peso della pallina nelle sue componenti: F/ che ha direzione tangente alla traiettoria descritta dalla pallina, e F⊥ che, invece, da direzione perpendicolare ad essa; notiamo che la tensione della fune è bilanciata dalla componente perpendicolare della forza-peso
e non mi sembra consideri alcuna apparente. SOlo peso e tensione che si elidono.
Spero mi aiuterai a capire, perché vorrei proprio riuscirci.
Un immenso grazie per il tuo aiuto!
Alticco
un pendolo semplice, appeso in ascensore accelerato verso l’alto con accelerazione di modulo $a$ , ha un periodo di oscillazione dato da :
$T = 2\pisqrt(l/(g+a))$
Se invece l’ascensore fosse in caduta libera, al denominatore sotto radice avresti $g-g =0$ , quindi matematicamente T =infinito. Cioè il pendolo non oscilla, il filo viene in bando. Nella ISS non puoi far oscillare pendoli.
un pendolo semplice, appeso in ascensore accelerato verso l’alto con accelerazione di modulo $a$ , ha un periodo di oscillazione dato da :
$T = 2\pisqrt(l/(g+a))$
Se invece l’ascensore fosse in caduta libera, al denominatore sotto radice avresti $g-g =0$ , quindi matematicamente T =infinito. Cioè il pendolo non oscilla, il filo viene in bando. Nella ISS non puoi far oscillare pendoli.
"Shackle":
Alticco
un pendolo semplice, appeso in ascensore accelerato verso l’alto con accelerazione di modulo $a$ , ha un periodo di oscillazione dato da :
$T = 2\pisqrt(l/(g+a))$
Se invece l’ascensore fosse in caduta libera, al denominatore sotto radice avresti $g-g =0$ , quindi matematicamente T =infinito. Cioè il pendolo non oscilla, il filo viene in bando. Nella ISS non puoi far oscillare pendoli.
Ti ringrazio, però non ho ben capito come risolva ilmio dubbio
"alticco":
Però non capisco: la tensione non è tutta forza centrifuga, è solo una parte di essa, perché una parte della tensione bilancia anche la forza peso. Quindi perché è sbagliato dire "una parte della tensione è la forza centripeta, infatti la tensione totale sommata vettorialemente alla forza peso danno come risultante la forza centripeta"?
"la tensione è la forza centripeta che" mi sembra quasi dire che la tensione è "=" forza centripeta, ma la tensione non finisce tutta in centripeta.
Hai due forze: la tensione del filo e la forza peso, la forza peso nel caso in oggetto non ha alcuna componente centripeta visto che comunque è opposta rispetto alla direzione verso il centro (centripeta è verso il centro per definizione).
"alticco":
Perché qui scrive
[.....]
Scomponiamo la forza-peso della pallina nelle sue componenti: F/ che ha direzione tangente alla traiettoria descritta dalla pallina, e F⊥ che, invece, da direzione perpendicolare ad essa; notiamo che la tensione della fune è bilanciata dalla componente perpendicolare della forza-peso
e non mi sembra consideri alcuna apparente. SOlo peso e tensione che si elidono.
Il discorso che ti ho fatto io nella seconda parte del mio messaggio precedente si riferisce al sistema di riferimento mobile non inerziale che vede la pallina ferma (e se vuoi il filo che le ruota attorno da una parte e dall'altra, così come il peso), nella trattazione qui che hai messo tu ci si riferisce invece a un sistema fisso, quindi ovvio che non ci siano forze apparenti.
È lo stesso punto di vista che ho usato io prima parlando di forza centripeta (non centrifuga).
EDIT:corretto alcune imprecisioni
Grazie mille, ho forse capito. La forza centripeta è tutta la forza diretta nel centro (quindi la tensione), pensavo che la forza centripeta fosse solo la parte di tensione che teneva in moto circolare la pallina appesa. Non so se mi spiego, però non consideravo la forza che compensava la forza peso. Invece mi sembra di capire che forza centripeta=tensione del filo. Giusto?
Se è così questo punto è risolto e ti ringrazio davvero tanto!
Per quanto riguarda il 2 problema.
Io avevo capito che quel sistema x,y centrato sulla pallina in moto si muovesse con essa (quella del disegno che ho postato).
Invece mi stai suggerendo che quel sistema nel diesgno sia fisso? Però anche così fosse non mi ritrovo nel senso che considera comunque due forze, ma io nella trattazione non vedo considerare una quota di forza utile. Mi spiego..
Dice:
"Scomponiamo la forza-peso della pallina nelle sue componenti: F/ che ha direzione tangente alla traiettoria descritta dalla pallina, e F⊥ che, invece, da direzione perpendicolare ad essa; notiamo che la tensione della fune è bilanciata dalla componente perpendicolare della forza-peso"
Tuttavia non è relamente bilanciata, perchédovrebbe esserci una parte di forzain più utile a dar origine all'accelerazione centripeta che tiene la pallina in moto circolare. Qui invece dice che "si bilanciano" (e bilanciano lo intendo come annullano no?) forza peso e tensione e non vedo il disavanzo di forza che dovrebbe dar origine ad $a_c$. Non riesco davvero a capire sono tristissimo.
Comunque il mio professsore ha preso questo diegno
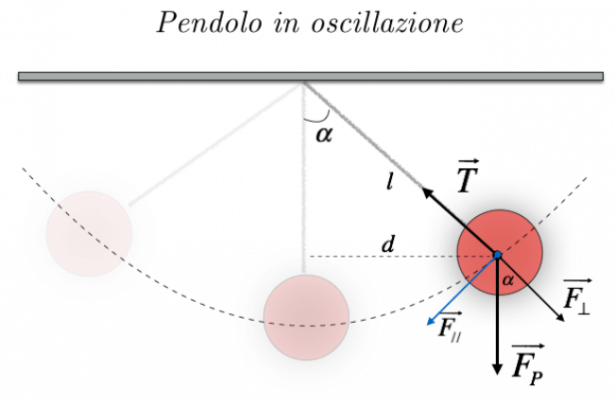
e mettiamo di considerare istante per istante il sistema di assi x,y che si muova assieme alla pallina appesa che ondeggia, così da avere origine sempre in essa.
Ecco, poi ha scomposto volta per volta le forze: una forza peso (scomposta lungo la radiale) e dice che si compensa con la tensione (compensa io la interpreto come si elidono vicendevolmente dando 0). Però qui io ci metterei anche la forza centrifuga così da vedere il perno ruotare attorno a me pallina, mentre il prof dice solo a=0 perché $F_p$ si compensa con $T$.
"Faussone":
"la tensione è la forza centripeta che" mi sembra quasi dire che la tensione è "=" forza centripeta, ma la tensione non finisce tutta in centripeta.
Grazie mille, ho forse capito. La forza centripeta è tutta la forza diretta nel centro (quindi la tensione), pensavo che la forza centripeta fosse solo la parte di tensione che teneva in moto circolare la pallina appesa. Non so se mi spiego, però non consideravo la forza che compensava la forza peso. Invece mi sembra di capire che forza centripeta=tensione del filo. Giusto?
Se è così questo punto è risolto e ti ringrazio davvero tanto!
Per quanto riguarda il 2 problema.
Io avevo capito che quel sistema x,y centrato sulla pallina in moto si muovesse con essa (quella del disegno che ho postato).
Invece mi stai suggerendo che quel sistema nel diesgno sia fisso? Però anche così fosse non mi ritrovo nel senso che considera comunque due forze, ma io nella trattazione non vedo considerare una quota di forza utile. Mi spiego..
Dice:
"Scomponiamo la forza-peso della pallina nelle sue componenti: F/ che ha direzione tangente alla traiettoria descritta dalla pallina, e F⊥ che, invece, da direzione perpendicolare ad essa; notiamo che la tensione della fune è bilanciata dalla componente perpendicolare della forza-peso"
Tuttavia non è relamente bilanciata, perchédovrebbe esserci una parte di forzain più utile a dar origine all'accelerazione centripeta che tiene la pallina in moto circolare. Qui invece dice che "si bilanciano" (e bilanciano lo intendo come annullano no?) forza peso e tensione e non vedo il disavanzo di forza che dovrebbe dar origine ad $a_c$. Non riesco davvero a capire
sono tristissimo.Comunque il mio professsore ha preso questo diegno
e mettiamo di considerare istante per istante il sistema di assi x,y che si muova assieme alla pallina appesa che ondeggia, così da avere origine sempre in essa.
Ecco, poi ha scomposto volta per volta le forze: una forza peso (scomposta lungo la radiale) e dice che si compensa con la tensione (compensa io la interpreto come si elidono vicendevolmente dando 0). Però qui io ci metterei anche la forza centrifuga così da vedere il perno ruotare attorno a me pallina, mentre il prof dice solo a=0 perché $F_p$ si compensa con $T$.
"alticco":
[.....]
Invece mi sembra di capire che forza centripeta=tensione del filo. Giusto?
Giusto.
"alticco":
Per quanto riguarda il 2 problema.
[....]
Se devo dirti la verità non si capisce molto da quanto riporti di quella trattazione, sarebbe da leggere bene tutto e non solo la parte che hai riportato per capire se ci sono errori e se la spiegazione non è proprio corretta...
Facciamo così, ti dico l'approccio corretto, rispetto a un sistema fisso, per arrivare all'equazione del pendolo.
Quando scrivi le equazioni tieni presente che devi sempre considerare come sono messi gli assi coordinati e quali variabili stai considerando.
L'approccio più semplice (che è quello che normalmente si adotta in fisica1 per il pendolo semplice) è di riferirsi a un asse che in pratica corrisponde a un asse curvilineo che segue l'arco di circonferenza, quindi $x$ è una coordinata curvilinea, mentre l'altro asse $y$ è diretto perpendicolarmente all'asse curvilineo e quindi rappresenta la direzione radiale.
Quindi quando scrivi nella direzione di questi due assi l'equazione di Newton hai (usando gli stessi simboli della figura che hai messo):
$mddot x=-mg sin alpha$
con $alpha=x/l$ (assumendo che $x=0$ corrisponda alla posizione verticale)
Poi supponendo "piccole oscillazioni" si ottiene la nota equazione:
$ddot x +g/l x=0$
(Questa equazione si ricava anche applicando la seconda equazione cardinale ovviamente.)
Invece per l'altra direzione (radiale) occorre ricordare che l'accelerazione è solo centripeta e risulta pari a $dot x^2 /l$ quindi:
$m dot x^2/l=T-mg cos alpha$
da cui, nota la legge oraria che fornisce $x$ (e quindi $alpha$) si ricava la tensione del filo.
(Osserva che $T$ è concorde con l'accelerazione centripeta visto che è verso il centro, mentre la componente del peso è opposta).
Un modo più rigoroso (capisco che riferirsi a questi assi curvilineo e radiale sembra poco preciso infatti) è quello di scrivere l'equazione di Newton usando le coordinate polari.
In pratica quindi la posizione di un punto generico nel nostro sistema di riferimento (sempre fisso) la identifichiamo con le coordinate $r$ e $alpha$ che danno la distanza dall'origine (centro di rotazione del pendolo nel caso specifico) e dall'angolo $alpha$ che dà la posizione angolare.
Per far questo bisogna fare attenzione però a scrivere bene in termini di $r$ e $alpha$ le velocità e accelerazioni nelle direzioni polari (se interessa lo possiamo vedere, ma non vorrei mettere troppa carne al fuoco).
Guarda sei stato chiarissimo. Direi che per quanto riguarda la trattazione con coordinata curvilinea non mi crea altri dubbi.
Mi mancava il capire la situazione iniziale, cioè non avevo proprio capito la storia dell'asse curvilineo e quindi immaginavo un continuo muoversi del sdr con la pallina.
Insomma, in realtà considero invece un asse x che approssima l'arco di circonferenza e un asse y a esso sempre perpendicolare e fissi!
Ecco l'inghippo!!
Mi piacerebbe tuttavia capire anche quella con coordinata polare. Mi piacerebbe davvero poterne leggere a riguardo una tua spiegazione.
RIesco a immaginare l'equazione del moto che possa essere (ci provo): $l(d^2theta)/(dt^2)=-gsintheta≃-g theta$ però non capisco come considerare l'asse radiale (cioè le forze su di esso).
Infatti c'è un punto che non ho compreso:
Non capisco infatti bene perché nelle polari sia sempre fisso il sdr. In teoria infatti il versore radiale non dovrebbe ruotare seguento la posizione della pallina in moto? Per questo immaginavo forze apparenti dovute al moto del versore radiale che mette in atto un sdr non inerziale rispetto al sdr laboratorio fisso.
Spero davvero avrai voglia di spiegarmi quello polare, ora sono assai curioso e mi stai aiutando moltissimo
L'approccio più semplice (che è quello che normalmente si adotta in fisica1 per il pendolo semplice) è di riferirsi a un asse che in pratica corrisponde a un asse curvilineo che segue l'arco di circonferenza, quindi x è una coordinata curvilinea, mentre l'altro asse y è diretto perpendicolarmente all'asse curvilineo e quindi rappresenta la direzione radiale
Mi mancava il capire la situazione iniziale, cioè non avevo proprio capito la storia dell'asse curvilineo e quindi immaginavo un continuo muoversi del sdr con la pallina.
Insomma, in realtà considero invece un asse x che approssima l'arco di circonferenza e un asse y a esso sempre perpendicolare e fissi!
Ecco l'inghippo!!
Mi piacerebbe tuttavia capire anche quella con coordinata polare. Mi piacerebbe davvero poterne leggere a riguardo una tua spiegazione.
RIesco a immaginare l'equazione del moto che possa essere (ci provo): $l(d^2theta)/(dt^2)=-gsintheta≃-g theta$ però non capisco come considerare l'asse radiale (cioè le forze su di esso).
Infatti c'è un punto che non ho compreso:
In pratica quindi la posizione di un punto generico nel nostro sistema di riferimento (sempre fisso)
Non capisco infatti bene perché nelle polari sia sempre fisso il sdr. In teoria infatti il versore radiale non dovrebbe ruotare seguento la posizione della pallina in moto? Per questo immaginavo forze apparenti dovute al moto del versore radiale che mette in atto un sdr non inerziale rispetto al sdr laboratorio fisso.
Spero davvero avrai voglia di spiegarmi quello polare, ora sono assai curioso e mi stai aiutando moltissimo
"alticco":
Mi piacerebbe tuttavia capire anche quella con coordinata polare. Mi piacerebbe davvero poterne leggere a riguardo una tua spiegazione.
[...]
Per capire quello intanto devi capire che lavorare in coordinate polari significa che invece di identificare un punto tramite le coordinate cartesiane classiche $x$ e $y$ (sto parlando proprio delle coordinate cartesiane non più della coordinata curvilinea che prima ho pure chiamato $x$), lo identifichi dalla distanza dall'origine $r$ e dall'angolo $alpha$ che il vettore posizione forma rispetto ad una certa posizione di riferimento.
Il legame tra le coordinate cartesiane e quelle polari possiamo prenderlo come:
$x=r sin alpha$
$y=-r cos alpha$
infatti per applicarlo al pendolo mi pare la scelta più naturale dell'angolo $alpha$ che coincide in questo modo con l'angolo del pendolo.
Ora dobbiamo trovare il legame tra velocità e accelerazioni in coordinate cartesiane e polari.
Derivando rispetto al tempo si ha:
$dot x=dot r sin alpha + r dot alpha cos alpha$
$dot y=-dot r cos alpha+r dot alpha sin alpha$
Però a noi serve scrivere queste componenti nella direzione radiale e circonferenziale che equivale a scrivere questo vettore rispetto a un riferimento ruotato di $90-alpha$ gradi in senso orario rispetto al riferimento cartesiano, in modo che le velocità siano appunto scritte nelle direzioni radiale e circonferenziale.
Questo equivale a applicare la matrice di rotazione:
\[
\begin{pmatrix} \sin\alpha & -\cos\alpha \\ \cos\alpha & \sin \alpha \end{pmatrix}
\]
Facendo i conti si trova
$v_r=dot r$
$v_alpha=r dot alpha$
Analogamente derivando ancora rispetto al tempo, calcolando quindi $ddotx$ e $ddot y$ e applicando nuovamente la matrice di rotazione si trova (se vuoi prova a fare i conti tu):
$a_r=ddot r - dot alpha^2r$
$a_alpha=ddot alpha r+2 dot alpha dot r$
A questo punto è molto semplice basta scrivere l'equazione di Newton in direzione radiale e circonferenziale:
$m a_r \equiv m (ddot r - dot alpha^2r)=mg cos alpha - T$
e visto che la massa è vincolata a stare sulla circonferenza $r=l$ ed è costante per cui in definitiva:
$T=m(g cos alpha + dot alpha^2 l)$
per la direzione circonferenziale invece:
$m a_alpha \equiv m(ddot alpha r + 2 dot alpha dot r)=-mg sin alpha$
anche stavolta ovviamente si ha che $r=l$ costante quindi:
$ddot alpha = -g/l sin alpha$
Abbiamo quindi ottenuto le relazioni equivalenti a quelle già viste prima.
Ti ringrazio, ho capito perfettamente come affrontare il problema e mi torna ogni singola formula, ho anche effettuato i calcoli sulle accelerazioni che consigliavi di svolgere e torna .
CHiedo solo 2 cose:
1) Mi piacerebbe chiarire un ultimo aspetto che mi turba, ovvero il fatto che in effetti sia un sdr fisso anche quello polare. Cerco di spiegare quello che mi confonde.
Io ho studiato un esempio di sdr non inerziale che è (prendiamo caso semplice) un sdr in moto rotatorio rispetto a un sdr fisso (che chiamo laboratorio per comodità).
Gli assi di quello che ruota, ruotano appunto rispetto aquello fisso e devo quindi derivare anche i versori nella loro rotazione, procedento con la derivata seconda giungo a accelerazone centrifuga e di coriolis.
Passiamo al sdr polare, qui mi confonde questo: il vettore radiale che congiunge oggetto all'origine (mettiamo il chiodo a cui appendo il filo) ruota così come ruota anche la direzione circonferenziale! Quindi perché questo non è un sdr in rotazione (e quindi NON inerziale)? Noi lo trattiamo come sdr fisso (quello polare) però non risco bene a capire profondamente il perché in quanto vedendo dei versori ruotare mi immaginavo la nascita di forze apparenti (tipo centrifuga). Mi sfugge questa faccenda.
E' quindi più una domanda di interpretazione del fenomeno, perché ripeto a formule mi torna bene.
2) Volevo poi chiederti un ultimo chiarimento su
Ho studiato solo lematrici di rotazione in AL che ruotano oggetti (cioè ruoto i vettori), mentre qui ruoto il sdr, perché il vettore velocità è lo stesso ma cambia solocome lo scompongo. Posso chiederti come si ricava tale matrice?
io conoscevo (che ruota il vettore)
\[
\begin{pmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos \alpha \end{pmatrix}
\]
Vorrei capire come si giunge alla tua.
Mi scuso se ho allungato un po' la discussione, però se non avessi chiesto qui e non avessi incontrato letue risposte sarei ancora pieno di mille dubbi. Prometto che capiti questi ultimi due dubbi non porrò altre domande su questo thread
Ti ringrazio ancora.
.CHiedo solo 2 cose:
1) Mi piacerebbe chiarire un ultimo aspetto che mi turba, ovvero il fatto che in effetti sia un sdr fisso anche quello polare. Cerco di spiegare quello che mi confonde.
Io ho studiato un esempio di sdr non inerziale che è (prendiamo caso semplice) un sdr in moto rotatorio rispetto a un sdr fisso (che chiamo laboratorio per comodità).
Gli assi di quello che ruota, ruotano appunto rispetto aquello fisso e devo quindi derivare anche i versori nella loro rotazione, procedento con la derivata seconda giungo a accelerazone centrifuga e di coriolis.
Passiamo al sdr polare, qui mi confonde questo: il vettore radiale che congiunge oggetto all'origine (mettiamo il chiodo a cui appendo il filo) ruota così come ruota anche la direzione circonferenziale! Quindi perché questo non è un sdr in rotazione (e quindi NON inerziale)? Noi lo trattiamo come sdr fisso (quello polare) però non risco bene a capire profondamente il perché in quanto vedendo dei versori ruotare mi immaginavo la nascita di forze apparenti (tipo centrifuga). Mi sfugge questa faccenda.
E' quindi più una domanda di interpretazione del fenomeno, perché ripeto a formule mi torna bene.
2) Volevo poi chiederti un ultimo chiarimento su
\[
\begin{pmatrix} \sin\alpha & -\cos\alpha \\ \cos\alpha & \sin \alpha \end{pmatrix}
\]
Ho studiato solo lematrici di rotazione in AL che ruotano oggetti (cioè ruoto i vettori), mentre qui ruoto il sdr, perché il vettore velocità è lo stesso ma cambia solocome lo scompongo. Posso chiederti come si ricava tale matrice?
io conoscevo (che ruota il vettore)
\[
\begin{pmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos \alpha \end{pmatrix}
\]
Vorrei capire come si giunge alla tua.
Mi scuso se ho allungato un po' la discussione, però se non avessi chiesto qui e non avessi incontrato letue risposte sarei ancora pieno di mille dubbi. Prometto che capiti questi ultimi due dubbi non porrò altre domande su questo thread
Ti ringrazio ancora.
"alticco":
1) Mi piacerebbe chiarire un ultimo aspetto che mi turba, [...]
Passiamo al sdr polare, qui mi confonde questo: il vettore radiale che congiunge oggetto all'origine (mettiamo il chiodo a cui appendo il filo) ruota così come ruota anche la direzione circonferenziale! Quindi perché questo non è un sdr in rotazione (e quindi NON inerziale)? Noi lo trattiamo come sdr fisso (quello polare) però non risco bene a capire profondamente il perché in quanto vedendo dei versori ruotare mi immaginavo la nascita di forze apparenti (tipo centrifuga). Mi sfugge questa faccenda.
Non capisco perché pensi che un sistema di riferimento polare debba essere mobile...
Col sistema cartesiano individui un punto con le due coordinate cartesiane $x$ e $y$ (facciamo sempre l'esempio 2D, ovviamente non ha importanza), mentre col sistema polare individui un punto tramite $r$ e $alpha$ (più comunemente si chiama $theta$ ho scelto di chiamarla $alpha$ per questo esempio specifico), tutto qui.
Ovvio che poi nello scrivere velocità e accelerazioni in termini di $v_r$ e $v_alpha$, e $a_r$ e $a_alpha$ bisogna fare attenzione alle direzioni ed è quello che abbiamo fatto con i conti che hai visto anche tu.
"alticco":
2) Volevo poi chiederti un ultimo chiarimento su
\[
\begin{pmatrix} \sin\alpha & -\cos\alpha \\ \cos\alpha & \sin \alpha \end{pmatrix}
\]
Ho studiato solo lematrici di rotazione in AL che ruotano oggetti (cioè ruoto i vettori), mentre qui ruoto il sdr, perché il vettore velocità è lo stesso ma cambia solocome lo scompongo. Posso chiederti come si ricava tale matrice?
io conoscevo (che ruota il vettore)
\[
\begin{pmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos \alpha \end{pmatrix}
\]
Vorrei capire come si giunge alla tua.
Non c'è differenza: la matrice che hai scritto tu ruota un vettore di $alpha$ in senso antiorario, o, in maniera equivalente, permette di scrivere le coordinate di un vettore rispetto ad un riferimento ruotato di $alpha$ in senso orario; quella che ho scritto io permette di scrivere il vettore rispetto ad un riferimento ruotato di $90-alpha$ in senso orario, o ruota il vettore di $90-alpha$ in senso antiorario.
Ok direi che anche per la matrice il dubbio è risolto. Ho visto che nel mentre hai già risposto ed ero giunto a questa conclusione. Grazie mille.
Questa invece è l'ultima parte che ancora mi sconquiffera. Diciamo che mi sembra rotante perche i versori "radiale" e "trasverso" (cioè quello tangente) mi pare che ruotino, quindi un sistema per cui i versori ruotano mi viene da immaginarlo rotante (esattamente come quando considero due sdr cartesiani uno in rotazione rispetto all'altro, dove le levelocità aggiuntive così come le accelerazioni, escono per derivazione di poisson dei versori che ruotano appunto). Quindi credo il problema sia proprio relativo alla mia comprensione del sdr in sé. Devo capire perché non ruoti se invece i loro versori ruotano.
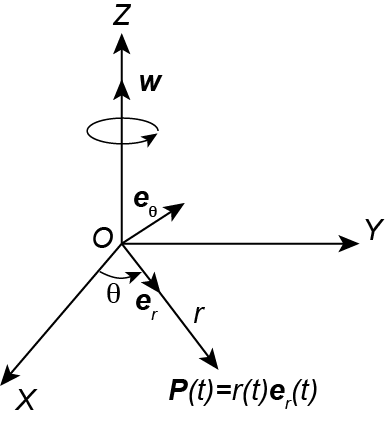
Forse una figura aiuta: $e_theta$ ed $e_r$ li vedo ortogonali e ruotare,un po' come fossero due versori che ruotano nel caso di rotazione di un sdr cartesiano rispetto a uno fisso da cui nascono le forze apparenti.
Volta per volta il punto P è individuato da un parametro r(t) che però ruota poiché il vettore r ruota.
Non so se mi sono spiegato meglio
PS: avevo cercato quella immagine su google e mi accorgo che appartiene al sito http://significatofisico.blogspot.com/2 ... ri_67.html che tra l'altro spiega esattamentr in modo più chiaro il mio dubbio, considerando le polari comeuna conseguenza di una rotazione e derivazione dei versori (se non fosse chiaro il mio scritto forse qui si legge meglio dovemi confondo).
"Faussone":
Non capisco perché pensi che un sistema di riferimento polare debba essere mobile...
Col sistema cartesiano individui un punto con le due coordinate cartesiane $x$ e $y$ (facciamo sempre l'esempio 2D, ovviamente non ha importanza), mentre col sistema polare individui un punto tramite $r$ e $alpha$ (più comunemente si chiama $theta$ ho scelto di chiamarla $alpha$ per questo esempio specifico), tutto qui.
Ovvio che poi nello scrivere velocità e accelerazioni in termini di $v_r$ e $v_alpha$, e $a_r$ e $a_alpha$ bisogna fare attenzione alle direzioni ed è quello che abbiamo fatto con i conti che hai visto anche tu.
Questa invece è l'ultima parte che ancora mi sconquiffera. Diciamo che mi sembra rotante perche i versori "radiale" e "trasverso" (cioè quello tangente) mi pare che ruotino, quindi un sistema per cui i versori ruotano mi viene da immaginarlo rotante (esattamente come quando considero due sdr cartesiani uno in rotazione rispetto all'altro, dove le levelocità aggiuntive così come le accelerazioni, escono per derivazione di poisson dei versori che ruotano appunto). Quindi credo il problema sia proprio relativo alla mia comprensione del sdr in sé. Devo capire perché non ruoti se invece i loro versori ruotano.
Forse una figura aiuta: $e_theta$ ed $e_r$ li vedo ortogonali e ruotare,un po' come fossero due versori che ruotano nel caso di rotazione di un sdr cartesiano rispetto a uno fisso da cui nascono le forze apparenti.
Volta per volta il punto P è individuato da un parametro r(t) che però ruota poiché il vettore r ruota.
Non so se mi sono spiegato meglio
PS: avevo cercato quella immagine su google e mi accorgo che appartiene al sito http://significatofisico.blogspot.com/2 ... ri_67.html che tra l'altro spiega esattamentr in modo più chiaro il mio dubbio, considerando le polari comeuna conseguenza di una rotazione e derivazione dei versori (se non fosse chiaro il mio scritto forse qui si legge meglio dovemi confondo).
"alticco":
Questa invece è l'ultima parte che ancora mi sconquiffera. Diciamo che mi sembra rotante perche i versori "radiale" e "trasverso" (cioè quello tangente) mi pare che ruotino, [....].
No quei versori non ruotano.
Il sistema di riferimento è fisso, semplicemente in un sistema cartesiano tu identifichi una posizione con $x$ e $y$, per esempio $x=1$ e $y=1$, mentre nel sistema polare identifichi lo stesso punto per esempio con $r=sqrt(2)$ $theta=pi/4 \equiv 45°$ (questa è la scelta che si fa normalmente per un sistema polare che è leggermente diversa da quella che ho fatto per il pendolo con l'angolo $alpha$, infatti l'angolo si può scegliere a partire da dove si vuole ovviamente).
Mettiamo poi che quel punto abbia velocità $dotx=1$ $doty=1$ in coordinate cartesiane, in coordinate polari la velocità sara $v_r=1$ $v_theta=0$, ma sia il sistema cartesiano che quello polare sono fermi.
Un altro punto potrebbe trovarsi nella posizione $x=1$ $y=0$ e muoversi con velocità $dotx=0$ $doty=1$ allora la posizione del punto in coordinate polari sarebbe $r=1$ $theta=0$ e la velocità $v_r=0$ $v_theta=1$ e così via.
EDIT
Nota che la velocità (e l'accelerazione) del punto in coordinate cartesiane non dipende dalla posizione del punto, mentre in coordinate polari sì, nel senso che se non sai la posizione del punto non puoi interpretare la velocità (o l'accelerazione) espressa nel riferimento polare, forse è questo che ti confonde....? Anche questo comunque non significa che il riferimento è rotante ovviamente. Prova a rifletterci da te, non credo posso dirti molto di più.
Ovvio che per un punto che ruota, come il pendolo appunto, è comodo, come abbiamo visto, lavorare in coordinate polari, oppure per un punto di cui si conosce il moto rispetto ad un sistema rotante può essere più comodo rappresentare il tutto in coordinate polari[nota]Vedi per esempio questa vecchia discussione in cui per scrivere le equazioni differenziali del moto nel sistema rotante è molto meglio lavorare in coordinate polari.[/nota], ma questo ultimo caso non significa che l'orientamento polare debba applicarsi solo ad un sistema di riferimento rotante (infatti abbiamo visto che per il pendolo il sistema è fisso appunto).
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo