Dubbi momento angolare e velocità angolare
Salve,
sto preparando l'esame di fisica generale ed ho un po' di dubbi riguardo questo esercizio:
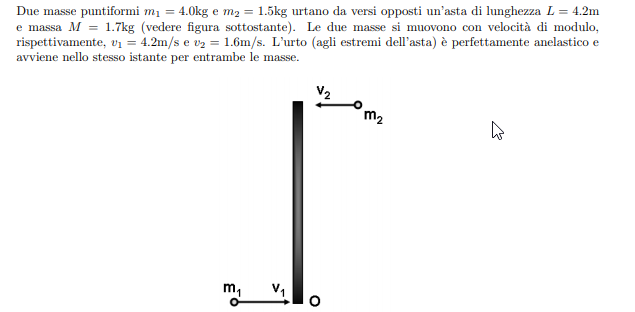
Il secondo punto di questo esercizio richiede di calcolare la velocità angolare del sistema subito dopo l'urto. Il primo dubbio è questo: non si dovrebbe conoscere qual è l'asse di rotazione attorno al quale ruota il sistema per calcolare la velocità angolare?
Questo punto inoltre viene risolto così:

Da qui il secondo dubbio: in questo modo quindi considera il sistema che ruota attorno al centro di massa? E se avessi considerato come polo un punto diverso dal centro di massa e mi fossi ricavato la velocità angolare allo stesso modo di quello fatto sopra, avrei ottenuto un risultato diverso?
Cioè, in generale, quando scrivo L = Iw, sto considerando come I il momento d'inerzia rispetto all'asse attorno a cui ruota il corpo rigido, e con w la velocità angolare attorno all'asse di rotazione?
sto preparando l'esame di fisica generale ed ho un po' di dubbi riguardo questo esercizio:

Il secondo punto di questo esercizio richiede di calcolare la velocità angolare del sistema subito dopo l'urto. Il primo dubbio è questo: non si dovrebbe conoscere qual è l'asse di rotazione attorno al quale ruota il sistema per calcolare la velocità angolare?
Questo punto inoltre viene risolto così:

Da qui il secondo dubbio: in questo modo quindi considera il sistema che ruota attorno al centro di massa? E se avessi considerato come polo un punto diverso dal centro di massa e mi fossi ricavato la velocità angolare allo stesso modo di quello fatto sopra, avrei ottenuto un risultato diverso?
Cioè, in generale, quando scrivo L = Iw, sto considerando come I il momento d'inerzia rispetto all'asse attorno a cui ruota il corpo rigido, e con w la velocità angolare attorno all'asse di rotazione?
Risposte
Intanto, il momento angolare si conserva se, come polo, si prende:
1. Un punto fisso.
2. Il centro di massa.
3. Un punto mobile avente, in ogni istante, velocità parallela al centro di massa.
Tipicamente, si prende il centro di massa. Prendere un altro polo, al netto di calcoli spesso più complicati, non farebbe alcuna differenza. Inoltre, la formula fondamentale della cinematica dei corpi rigidi:
è applicabile qualunque sia O. Tuttavia, poiché il moto del centro di massa è governato da tutte le forze esterne che agiscono sul corpo rigido, ciò che "balza all'occhio" è la rotazione rispetto al centro di massa. Solo per fare un esempio, si può considerare il moto di un'asta soggetta alla forza peso. In questo caso, ciò che balza all'occhio è la rotazione rispetto al centro di massa che si muove di moto parabolico. Più semplicemente, nell'esercizio proposto, visto che il sistema è isolato, ciò che balza all'occhio è la rotazione rispetto al centro di massa che si muove di moto rettilineo uniforme.
1. Un punto fisso.
2. Il centro di massa.
3. Un punto mobile avente, in ogni istante, velocità parallela al centro di massa.
Tipicamente, si prende il centro di massa. Prendere un altro polo, al netto di calcoli spesso più complicati, non farebbe alcuna differenza. Inoltre, la formula fondamentale della cinematica dei corpi rigidi:
$vecv_P=vecv_O+vec\omegaxx(P-O)$
è applicabile qualunque sia O. Tuttavia, poiché il moto del centro di massa è governato da tutte le forze esterne che agiscono sul corpo rigido, ciò che "balza all'occhio" è la rotazione rispetto al centro di massa. Solo per fare un esempio, si può considerare il moto di un'asta soggetta alla forza peso. In questo caso, ciò che balza all'occhio è la rotazione rispetto al centro di massa che si muove di moto parabolico. Più semplicemente, nell'esercizio proposto, visto che il sistema è isolato, ciò che balza all'occhio è la rotazione rispetto al centro di massa che si muove di moto rettilineo uniforme.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo