Corpi rigidi in rotazione
Salve, chiedo un aiuto per questo esercizio:
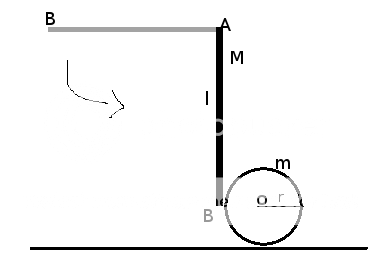
Un'asta AB sottile ed omogenea di massa M e lunga l, imperniata in A e libera di ruotare attorno ad un asse orizzontale per A, viene abbandonata con velocità nulla dalla posizione orizzontale. Quando raggiunge la posizione verticale l'estremo B urta una sfera all'altezza di O. La sfera ha massa m e raggio r.
a- Supposto l'urto perfettamente elastico determinare la velocità angolare dell'asta e la velocità della sfera immediatamente dopo l'urto.
b- Nel caso di urto completamente anelastico determinare la velocità angolare del sistema immediatamente dopo l'urto.
c- Spiegare perchè la sfera non rotola dopo l'urto anche se il piano orizzontale fosse scabro.
Io l'ho risolto così:
Lasciando cadere l'asta con velocità iniziale nulla si conserva l'energia meccanica $Mlg=1/6Ml^2\omega^2+mgl/2$ da cui $\omega=sqrt((3g)/l)$
Se l'urto è elastico si conserva l'energia cinetica prima e dopo l'urto $1/2I\omega^2+1/2mv^2=0$ da cui $v=sqrt((I\omega^2)/m)=sqrt((Mlg)/m)$
Se l'urto è anelastico i corpi restano attaccati dopo l'urto, l'energia non si conserva (per la presenza del vincolo in A)ma si conserva il momento angolare $I_(asta)\omega_(asta)=(I_(asta)+I_( Sfera))\omega_(sistema)$ da cui si ricava $\omega_(sistema)$.
Quello che non so è come trattare il momento di inerzia della sfera: so di dover usare Huygens-Steiner, ma non so come applicarlo... per la distanza dell'asse devo usare l'ipotenusa del triangolo che ha per cateti il raggio della sfera e la lunghezza dell'asta?
La risposta al punto c non la so, c'entra il fatto che la sfera è colpita all'altezza del centro di massa?
Ringrazio già da ora chi mi aiuterà.
Un'asta AB sottile ed omogenea di massa M e lunga l, imperniata in A e libera di ruotare attorno ad un asse orizzontale per A, viene abbandonata con velocità nulla dalla posizione orizzontale. Quando raggiunge la posizione verticale l'estremo B urta una sfera all'altezza di O. La sfera ha massa m e raggio r.
a- Supposto l'urto perfettamente elastico determinare la velocità angolare dell'asta e la velocità della sfera immediatamente dopo l'urto.
b- Nel caso di urto completamente anelastico determinare la velocità angolare del sistema immediatamente dopo l'urto.
c- Spiegare perchè la sfera non rotola dopo l'urto anche se il piano orizzontale fosse scabro.

Io l'ho risolto così:
Lasciando cadere l'asta con velocità iniziale nulla si conserva l'energia meccanica $Mlg=1/6Ml^2\omega^2+mgl/2$ da cui $\omega=sqrt((3g)/l)$
Se l'urto è elastico si conserva l'energia cinetica prima e dopo l'urto $1/2I\omega^2+1/2mv^2=0$ da cui $v=sqrt((I\omega^2)/m)=sqrt((Mlg)/m)$
Se l'urto è anelastico i corpi restano attaccati dopo l'urto, l'energia non si conserva (per la presenza del vincolo in A)ma si conserva il momento angolare $I_(asta)\omega_(asta)=(I_(asta)+I_( Sfera))\omega_(sistema)$ da cui si ricava $\omega_(sistema)$.
Quello che non so è come trattare il momento di inerzia della sfera: so di dover usare Huygens-Steiner, ma non so come applicarlo... per la distanza dell'asse devo usare l'ipotenusa del triangolo che ha per cateti il raggio della sfera e la lunghezza dell'asta?
La risposta al punto c non la so, c'entra il fatto che la sfera è colpita all'altezza del centro di massa?
Ringrazio già da ora chi mi aiuterà.
Risposte
up
ma non c'è nessuno che mi voglia aiutare?
non credo che sia un esercizio così complesso che nessuno di voi lo sappia risolvere... nessuno che voglia darmi una mano?
non credo che sia un esercizio così complesso che nessuno di voi lo sappia risolvere... nessuno che voglia darmi una mano?
Ciao lady, rispondo al tuo accorato appello, e mi riferisco al quesito 3 soltanto, che mi sembra quello che più ti lascia in dubbio ( i primi due, neanche li ho guardati, sono un pelandrone, scusami....)
Considera la palla un attimo dopo l'urto. Che cosa è successo nell'urto? È successo che per un brevissimo tempo $dt$ la palla ha ricevuto un impulso $F*dt = m *dv$ ( non lo voglio neanche sapere quanto vale $F$, ma dipende dai calcoli precedenti....), che fa variare la sua quantità di moto e cioè la sua velocità di $dv$. Ma immediatamente dopo l'urto, la Forza cessa di esistere sulla palla, che ha acquistato velocità, quindi energia cinetica! Come è questa velocità? È la velocità acquisita dal centro di massa della palla, parallela al piano.
Sappiamo che si può esprimere il momento angolare di un corpo rigido rispetto ad un polo fisso $O$ come somma di due termini : il momento angolare corrispondente al moto del cdm $C$ del corpo rigido più il momento angolare nel moto del corpo rispetto al suo cdm: questo secondo termine, esiste nel nostro caso immediatamente dopo l'urto?
Prendiamo un polo fisso $O$ sul piano, e scriviamo il momento angolare della palla rispetto ad $O$, nel modo più generale possibile come abbiamo detto prima :
$vecL = vecr\timesMvecv_c + vec(I_c\omega)$
dove $I_c$ è il momento di inerzia della palla rispetto ad un asse parallelo al piano e passante per il cdm.
Ora, sappiamo per la 2º eq Cardinale della Dianmica che si può avere variazione del momento angolare se agise un momento di forze esterne. Immediatamente dopo l'urto, avendo la palla acquistato la velocità $v_c$, esiste certamente il primo termine al secondo membro del momento. Ma qual è l'unica forza agente dopo l'urto sulla palla? È la forza di attrito col piano. Questa forza esiste, poiché il piano è scabro.
Però la retta di azione di questa forza passa per il polo $O$ che abbiamo assunto sul piano. Il momento della forza di attrito rispetto a questo polo dunque è zero.
Sulla palla (ripeto che stiamo parlando di una situazione ideale, e di quello che succede subito dopo l'urto) dopo l'urto non c'è alcun momento di forze esterne capace di indurre variazione del momento angolare iniziale.
(peso e reazione del piano si fanno equilibrio).
Quindi il momento angolare iniziale deve valere solo :
$vecL = vecr\timesMvecv_c $
il termine contenente $\omega$ è zero inizialmente. E per la conservazione di $vecL$, è zero anche per un po'.
Percio almeno inizialmente la palla striscia sul piano, e nello strisciare si consuma energia.
Sembra un nonsenso! Infatti la nostra comune esperienza qual è? È che la palla si mette a rotolare quasi subito: ma noi abbiamo a che fare con palle reali, deformabili, e piani anch'essi deformabili. E poi, un urto perfettamente centrato...sarà mai possibile?
Naturamente spero di non aver detto sciocchezze, nel qual caso qualcuno che mi corregge ci sarà senz'altro, vedrai.
Considera la palla un attimo dopo l'urto. Che cosa è successo nell'urto? È successo che per un brevissimo tempo $dt$ la palla ha ricevuto un impulso $F*dt = m *dv$ ( non lo voglio neanche sapere quanto vale $F$, ma dipende dai calcoli precedenti....), che fa variare la sua quantità di moto e cioè la sua velocità di $dv$. Ma immediatamente dopo l'urto, la Forza cessa di esistere sulla palla, che ha acquistato velocità, quindi energia cinetica! Come è questa velocità? È la velocità acquisita dal centro di massa della palla, parallela al piano.
Sappiamo che si può esprimere il momento angolare di un corpo rigido rispetto ad un polo fisso $O$ come somma di due termini : il momento angolare corrispondente al moto del cdm $C$ del corpo rigido più il momento angolare nel moto del corpo rispetto al suo cdm: questo secondo termine, esiste nel nostro caso immediatamente dopo l'urto?
Prendiamo un polo fisso $O$ sul piano, e scriviamo il momento angolare della palla rispetto ad $O$, nel modo più generale possibile come abbiamo detto prima :
$vecL = vecr\timesMvecv_c + vec(I_c\omega)$
dove $I_c$ è il momento di inerzia della palla rispetto ad un asse parallelo al piano e passante per il cdm.
Ora, sappiamo per la 2º eq Cardinale della Dianmica che si può avere variazione del momento angolare se agise un momento di forze esterne. Immediatamente dopo l'urto, avendo la palla acquistato la velocità $v_c$, esiste certamente il primo termine al secondo membro del momento. Ma qual è l'unica forza agente dopo l'urto sulla palla? È la forza di attrito col piano. Questa forza esiste, poiché il piano è scabro.
Però la retta di azione di questa forza passa per il polo $O$ che abbiamo assunto sul piano. Il momento della forza di attrito rispetto a questo polo dunque è zero.
Sulla palla (ripeto che stiamo parlando di una situazione ideale, e di quello che succede subito dopo l'urto) dopo l'urto non c'è alcun momento di forze esterne capace di indurre variazione del momento angolare iniziale.
(peso e reazione del piano si fanno equilibrio).
Quindi il momento angolare iniziale deve valere solo :
$vecL = vecr\timesMvecv_c $
il termine contenente $\omega$ è zero inizialmente. E per la conservazione di $vecL$, è zero anche per un po'.
Percio almeno inizialmente la palla striscia sul piano, e nello strisciare si consuma energia.
Sembra un nonsenso! Infatti la nostra comune esperienza qual è? È che la palla si mette a rotolare quasi subito: ma noi abbiamo a che fare con palle reali, deformabili, e piani anch'essi deformabili. E poi, un urto perfettamente centrato...sarà mai possibile?
Naturamente spero di non aver detto sciocchezze, nel qual caso qualcuno che mi corregge ci sarà senz'altro, vedrai.
[size=150]Sono appena tornato da un esame, dunque spero di aiutarti bene e di non dirti bischerate.[/size]
Sì. Immagino che a secondo membro tu volesi scrivere $M$... Questo subito prima dell'urto, però.
E io che ne so se non mi scrivi $I$ di chi eccetera?
Poi... Hai due incognite ($omega$ dell'asta e $v$ del cdm della sfera), quindi ti servono due equazioni. Io imporrei entrambe le conservazioni, ma non ho provato su carta dunque non so se basta e/o se funziona.
Direi di sì, avendo scelto $A$ come polo per la rotazione dell'intero sistema.
Ah, dire che "rimangono attaccate" è davvero poco scientifico. È migliore un "costituiscono un unico corpo in movimento".
Mmmh... Non vorrei direi una cavolata, ma possiamo (credo) supporre la forza esercitata nell'urto nel punto di contatto parallela al suolo. Se così fosse, se si vuole calcolare il suo momento $tau$ rispetto al centro di massa della sfera (poiché se ruota, essa ruoterà attorno a tale punto) esso risulta essere nullo. Dunque a causa di questa forza la sfera non ruoterà. Direi che, immediatamente dopo l'urto, questa è l'unica forza significativa in gioco (cioè, esiste un intorno temporale del momento dell'urto in cui l'attrito è trascurabile rispetto alla forza impulsiva dovuta all'urto), poiché l'attrito in quanto forza esterna è trascurabile durante l'urto, e, dunque, per un piccolo intervallo temporale dopo l'orto la sfera non ruoterà
Il tuo ragionamento, navigatore, ad occhio (e, dunque, probabilmente mi sbaglio), non mi convince perché, sempre ad occhio (quindi sempre potenzialmente mi trovo in errore), mi sembra decada se scegliamo un altro punto come polo, ad esempio il centro di massa.
Secondo me, ma potrei sbagliarmi, la risposta sta nella natura delle forze in gioco durante l'urto: esterna per l'attrito, e dunque trascurabile durante esso, interna per l'altra, che supporrei parallela al suolo, ma correggimi, navigatore, se sbaglio.
"ladidely":
Lasciando cadere l'asta con velocità iniziale nulla si conserva l'energia meccanica $Mlg=1/6Ml^2\omega^2+mgl/2$ da cui $\omega=sqrt((3g)/l)$
Sì. Immagino che a secondo membro tu volesi scrivere $M$... Questo subito prima dell'urto, però.
"ladidely":
Se l'urto è elastico si conserva l'energia cinetica prima e dopo l'urto $1/2I\omega^2+1/2mv^2=0$ da cui $v=sqrt((I\omega^2)/m)=sqrt((Mlg)/m)$
E io che ne so se non mi scrivi $I$ di chi eccetera?
Poi... Hai due incognite ($omega$ dell'asta e $v$ del cdm della sfera), quindi ti servono due equazioni. Io imporrei entrambe le conservazioni, ma non ho provato su carta dunque non so se basta e/o se funziona.
"ladidely":
Se l'urto è anelastico i corpi restano attaccati dopo l'urto, l'energia non si conserva (per la presenza del vincolo in A)ma si conserva il momento angolare $I_(asta)\omega_(asta)=(I_(asta)+I_( Sfera))\omega_(sistema)$ da cui si ricava $\omega_(sistema)$.
Quello che non so è come trattare il momento di inerzia della sfera: so di dover usare Huygens-Steiner, ma non so come applicarlo... per la distanza dell'asse devo usare l'ipotenusa del triangolo che ha per cateti il raggio della sfera e la lunghezza dell'asta?
Direi di sì, avendo scelto $A$ come polo per la rotazione dell'intero sistema.
Ah, dire che "rimangono attaccate" è davvero poco scientifico. È migliore un "costituiscono un unico corpo in movimento".
"ladidely":
La risposta al punto c non la so, c'entra il fatto che la sfera è colpita all'altezza del centro di massa?
Ringrazio già da ora chi mi aiuterà.
Mmmh... Non vorrei direi una cavolata, ma possiamo (credo) supporre la forza esercitata nell'urto nel punto di contatto parallela al suolo. Se così fosse, se si vuole calcolare il suo momento $tau$ rispetto al centro di massa della sfera (poiché se ruota, essa ruoterà attorno a tale punto) esso risulta essere nullo. Dunque a causa di questa forza la sfera non ruoterà. Direi che, immediatamente dopo l'urto, questa è l'unica forza significativa in gioco (cioè, esiste un intorno temporale del momento dell'urto in cui l'attrito è trascurabile rispetto alla forza impulsiva dovuta all'urto), poiché l'attrito in quanto forza esterna è trascurabile durante l'urto, e, dunque, per un piccolo intervallo temporale dopo l'orto la sfera non ruoterà
Il tuo ragionamento, navigatore, ad occhio (e, dunque, probabilmente mi sbaglio), non mi convince perché, sempre ad occhio (quindi sempre potenzialmente mi trovo in errore), mi sembra decada se scegliamo un altro punto come polo, ad esempio il centro di massa.
Secondo me, ma potrei sbagliarmi, la risposta sta nella natura delle forze in gioco durante l'urto: esterna per l'attrito, e dunque trascurabile durante esso, interna per l'altra, che supporrei parallela al suolo, ma correggimi, navigatore, se sbaglio.
E tutto il forum fa le congratulazioni a Giulio, che ha superato brillantemente l'esame!
È come avevo pensato io, e cioè che solo per un po' di tempo dopo l'urto il moto è soltanto traslatorio...la traccia del problema d'altronde dice : "dimostrare che la palla non ruota pur se il piano è scabro". Dunque mi sembrava opportuno richiamare qualche legge di conservazione : se è nullo inizialmente il momento angolare proprio (cioè rispetto al cdm), l'urto centrato non potrà modificarlo, e quindi la velocità angolare rimane nulla, e la palla trasla strisciando sul piano,almeno inizialmente, e strisciando perde energia.
È chiaro che in una situazione ideale, di piano e sfera perfettamente lisci, il moto dopo l'urto centrato sarebbe solo traslatorio, come una boccia liscissima lanciata senza imprimere rotazione sopra una liscissima superficie di un lago ghiacciato....quindi quello che dice il testo, e cioè che la palla non ruota anche se il piano è scabro, suggerisce che non c'è differenza, in questo caso, tra piano liscio e piano scabro....Giusta osservazione la tua, circa il momento angolare della forza di attrito rispetto al centro di massa, che non è certamente nullo...
Ma una cosa è certa: mentre è chiaro che la palla acquisisce nell'urto la "componente traslatoria" del momento angolare $M*v_c*r$, è anche chiaro che non acquisisce quella rotatoria, cioè $I_c*\omega$, almeno inizialmente, e cioè non ruota.
E questo mi suggerisce invece un'altra cosa: l'attrito iniziale è quello cinematico, non quello statico. La forza di attrito cinematico deve essere abbastanza consistente, non piccola, per superare l'attrito statico. Ma l'attrito cinematico consuma energia, la palla rallenta, e quindi in effetti c'è una variazione di $v_c$ e perciò anche della parte traslatoria $m*v_c*r$ del momento angolare...a un certo punto cessa il moto relativo tra palla e piano (lo strisciamento) e entra in gioco l'attrito statico : a questo punto, la sfera comincia a rotolare. Quindi la traccia dell'esercizio è un po' monca, secondo me....
Che ne pensi?
Mmmh... Non vorrei direi una cavolata, ma possiamo (credo) supporre la forza esercitata nell'urto nel punto di contatto parallela al suolo. Se così fosse, se si vuole calcolare il suo momento $tau$ rispetto al centro di massa della sfera (poiché se ruota, essa ruoterà attorno a tale punto) esso risulta essere nullo. Dunque a causa di questa forza la sfera non ruoterà. Direi che, immediatamente dopo l'urto, questa è l'unica forza significativa in gioco (cioè, esiste un intorno temporale del momento dell'urto in cui l'attrito è trascurabile rispetto alla forza impulsiva dovuta all'urto), poiché l'attrito in quanto forza esterna è trascurabile durante l'urto, e, dunque, per un piccolo intervallo temporale dopo l'orto la sfera non ruoterà
È come avevo pensato io, e cioè che solo per un po' di tempo dopo l'urto il moto è soltanto traslatorio...la traccia del problema d'altronde dice : "dimostrare che la palla non ruota pur se il piano è scabro". Dunque mi sembrava opportuno richiamare qualche legge di conservazione : se è nullo inizialmente il momento angolare proprio (cioè rispetto al cdm), l'urto centrato non potrà modificarlo, e quindi la velocità angolare rimane nulla, e la palla trasla strisciando sul piano,almeno inizialmente, e strisciando perde energia.
Il tuo ragionamento, navigatore, ad occhio (e, dunque, probabilmente mi sbaglio), non mi convince perché, sempre ad occhio (quindi sempre potenzialmente mi trovo in errore), mi sembra decada se scegliamo un altro punto come polo, ad esempio il centro di massa.
Secondo me, ma potrei sbagliarmi, la risposta sta nella natura delle forze in gioco durante l'urto: esterna per l'attrito, e dunque trascurabile durante esso, interna per l'altra, che supporrei parallela al suolo, ma correggimi, navigatore, se sbaglio.
È chiaro che in una situazione ideale, di piano e sfera perfettamente lisci, il moto dopo l'urto centrato sarebbe solo traslatorio, come una boccia liscissima lanciata senza imprimere rotazione sopra una liscissima superficie di un lago ghiacciato....quindi quello che dice il testo, e cioè che la palla non ruota anche se il piano è scabro, suggerisce che non c'è differenza, in questo caso, tra piano liscio e piano scabro....Giusta osservazione la tua, circa il momento angolare della forza di attrito rispetto al centro di massa, che non è certamente nullo...
Ma una cosa è certa: mentre è chiaro che la palla acquisisce nell'urto la "componente traslatoria" del momento angolare $M*v_c*r$, è anche chiaro che non acquisisce quella rotatoria, cioè $I_c*\omega$, almeno inizialmente, e cioè non ruota.
E questo mi suggerisce invece un'altra cosa: l'attrito iniziale è quello cinematico, non quello statico. La forza di attrito cinematico deve essere abbastanza consistente, non piccola, per superare l'attrito statico. Ma l'attrito cinematico consuma energia, la palla rallenta, e quindi in effetti c'è una variazione di $v_c$ e perciò anche della parte traslatoria $m*v_c*r$ del momento angolare...a un certo punto cessa il moto relativo tra palla e piano (lo strisciamento) e entra in gioco l'attrito statico : a questo punto, la sfera comincia a rotolare. Quindi la traccia dell'esercizio è un po' monca, secondo me....
Che ne pensi?
Credo di essere d'accordo, specie sul fatto che la traccia dell'esercizio non spiega molto bene cosa vuole, né le condizioni in cui le vuole. Comunque sì, mi trovo d'accordo sul fatto che, se il piano è scabro, non ruoterà solo per poco dopo l'urto per il motivo suesposto, in forma diversa, da entrambi.
Solo una cosa: mi piace molto poco la dicitura <<"componente traslatoria" del momento angolare>>, anche perché non ho ben chiaro cosa intendi.
Solo una cosa: mi piace molto poco la dicitura <<"componente traslatoria" del momento angolare>>, anche perché non ho ben chiaro cosa intendi.
prima di tutto vi ringrazio di avermi risposto.
in effetti ho sbagliato a scrivere tutta la formula...
comunque la ricavo da $Mlg=1/6Ml^2\omega^2+mgl^2$ no?
è quello dell'asta... non l'ho specificato perchè l'esercizio diceva subito che la sfera non ruota, quindi pensavo fosse non fraintendibile.
non si deve usare l'$\omega$ ricavata prima dalla conservazione dell'energia meccanica?
riguardo al terzo punto ho ancora un po' di confusione... scrivo quello che penso di aver capito, ditemi se è giusto: il momento angolare si calcola in generale come $L=rxxmv_c+I_c\omega$, in cui $rxxmv_c$ è data dalla forza impulsiva presente durante l'urto, quindi la sfera si muove di moto traslatorio, $I_c\omega=0$ invece, perchè dopo l'urto agisce solo la forza di attrito che ha momento nullo (non ho capito bene se si deve considerare la forza di attrito trascurabile o il suo momento nullo, in effetti...) quindi non ruota. Riguardo all'attrito poi mi servirebbe un chiarimento: ho studiato l'attrito statico, dinamico, viscoso, volvente ma non avevo mai sentito "attrito cinematico"... qualche parola in proposito?
scusate il mio pessimo linguaggio, giuro che d'ora in poi cercherò di utilizzare più adeguato, grazie anche per questo appunto
"giuliofis":
Sì. Immagino che a secondo membro tu volesi scrivere M... Questo subito prima dell'urto, però.
in effetti ho sbagliato a scrivere tutta la formula...
comunque la ricavo da $Mlg=1/6Ml^2\omega^2+mgl^2$ no?
"giuliofis":
E io che ne so se non mi scrivi I di chi eccetera?
è quello dell'asta... non l'ho specificato perchè l'esercizio diceva subito che la sfera non ruota, quindi pensavo fosse non fraintendibile.
"giuliofis":
Poi... Hai due incognite (ω dell'asta e v del cdm della sfera), quindi ti servono due equazioni. Io imporrei entrambe le conservazioni, ma non ho provato su carta dunque non so se basta e/o se funziona.
non si deve usare l'$\omega$ ricavata prima dalla conservazione dell'energia meccanica?
riguardo al terzo punto ho ancora un po' di confusione... scrivo quello che penso di aver capito, ditemi se è giusto: il momento angolare si calcola in generale come $L=rxxmv_c+I_c\omega$, in cui $rxxmv_c$ è data dalla forza impulsiva presente durante l'urto, quindi la sfera si muove di moto traslatorio, $I_c\omega=0$ invece, perchè dopo l'urto agisce solo la forza di attrito che ha momento nullo (non ho capito bene se si deve considerare la forza di attrito trascurabile o il suo momento nullo, in effetti...) quindi non ruota. Riguardo all'attrito poi mi servirebbe un chiarimento: ho studiato l'attrito statico, dinamico, viscoso, volvente ma non avevo mai sentito "attrito cinematico"... qualche parola in proposito?
"giuliofis":
Ah, dire che "rimangono attaccate" è davvero poco scientifico. È migliore un "costituiscono un unico corpo in movimento".
scusate il mio pessimo linguaggio, giuro che d'ora in poi cercherò di utilizzare più adeguato, grazie anche per questo appunto

"ladidely":
perchè dopo l'urto agisce solo la forza di attrito che ha momento nullo
Rispetto al centro di massa il suo momento è tutt'altro che nullo. Ma in un intorno temporale dell'urto l'attrito risulta a tutti gli effetti trascurabile.
"ladidely":
ho studiato l'attrito statico, dinamico, viscoso, volvente ma non avevo mai sentito "attrito cinematico"... qualche parola in proposito?
Cinetico, cinematico, dinamico... In sostanza, attrito legato al movimento traslatorio.
"giuliofis":
Cinetico, cinematico, dinamico... In sostanza, attrito legato al movimento traslatorio.
ah, ok, grazie.
"giuliofis":
Rispetto al centro di massa il suo momento è tutt'altro che nullo. Ma in un intorno temporale dell'urto l'attrito risulta a tutti gli effetti trascurabile.
ma perchè l'attrito risulta trascurabile? è dovuto al fatto che le forze impulsive che si sviluppano durante l'urto sono molto intense e perciò in un primo momento contano più queste che l'attrito?

Sì, è la definizione di urto. La trovi anche su Wikipedia.
grazie mille, per il terzo punto adesso è tutto chiaro.
per il secondo punto invece non mi è chiaro se devo impostare nuove equazioni o posso usare l'$\omega$ che avevo calcolato precedentemente.
per il secondo punto invece non mi è chiaro se devo impostare nuove equazioni o posso usare l'$\omega$ che avevo calcolato precedentemente.
Con "componente traslatoria del momento angolare" , che forse non è una espressione felice, intendevo dire la parte di momento angolare $vec((C- 0))\timesMvecv_c$ legata alla traslazione della palla con velocità $vecv_c$ del centro di massa, il cui modulo $Mv_cr$ rimane costante se la velocità $v_c$ del cdm è costante. L'altra parte $vec(I_c\omega)$ è quella legata al moto rotatorio attorno a un asse della palla perpendicolare al piano del foglio, che inizialmente è nulla.
Ma più ci penso, e più penso che questo esercizio è quanto meno impreciso, secondo me...
Ma più ci penso, e più penso che questo esercizio è quanto meno impreciso, secondo me...
"ladidely":
grazie mille, per il terzo punto adesso è tutto chiaro.
per il secondo punto invece non mi è chiaro se devo impostare nuove equazioni o posso usare l'$\omega$ che avevo calcolato precedentemente.
Quella calcolata precedentemente si riferisce al momento prima dell'urto (che ti serve), mentre a te interessa al momento successivo. Per la "seconda parte" del punto (a) prova ad impostare entrambe le conservazioni. Ti ripeto, però, che io non ho provato su carta. Ma, ad occhio, questa è la strada che tenterei io.
Non ce la faccio però a stare troppo dietro al forum in questi giorni.
Ma più ci penso, e più penso che questo esercizio è quanto meno impreciso, secondo me...
Concordo. E trovare esercizi imprecisi non sarebbe la prima volta.
Ho trovato questa esauriente dispensa sul web, che parla di rotolamento e strisciamento in termini rigorosamente matematici. Conosco l'autore, è uno in gamba.
http://www.ing.unitn.it/~siboni/dispenseMRvo/disco.pdf
http://www.ing.unitn.it/~siboni/dispenseMRvo/disco.pdf
ho rifatto tutti i calcoli, riscrivo tutto l'esercizio sperando che sia giusto:
l'asta è lasciata cadere con velocità nulla quindi per la conservazione dell'energia meccanica
$Mlg=1/6Ml^2\omega_i^2+Mgl/2$ da cui $\omega_i=sqrt(3g/l)$
se l'urto è elastico si conservano sia l'energia cinetica che il momento angolare
chiamando $I$ il momento angolare dell'asta
$\{(1/2I\omega^2+1/2mv^2=0),(I\omega_i=mrv+I\omega):}$
$\{(1/6Ml^2\omega^2+1/2mv^2=0),(1/3Ml^2\omega_i=mrv+1/3Ml^2\omega):}$
da cui, saltanto tutti i passaggi
${(\omega=(Ml^2\omega_i)/(3r^2+Ml^2)+-sqrt((Ml^2\omega_i)/(r^2+1/3Ml^2))),(v=1/3Ml^2(\omega_i-\omega)/(mr)):}$
se l'urto è totalmente anelastico si conserva solo il momento angolare, dopo l'urto la sfera e l'asta si muovono come un unico corpo e la sfera ruota attorno all'ipotenusa del triangolo che ha per cateti il raggio della sfera e l'asta.
chiamando $I_s$ il momento di inerzia della sfera
$1/3Ml^2\omega_i=(I+I_s)\omega_f$
$1/3Ml^2\omega_i={1/3Ml^2+[2/5mr^2+(l^2+r^2)m]}\omega_f$
da cui $\omega_f=(Ml^2\omega_i)/(3[(1/3M+m)l^2+7/5mr^2])$
ok, allora ti ringrazio per tutto il tempo che hai speso con il mio esercizio
ti ringrazio tanto, me la studierò come si deve
e sapere che l'esercizio è preso da un compito d'esame fa davvero molto piacere...](/datas/uploads/forum/emoji/eusa_wall.gif)
l'asta è lasciata cadere con velocità nulla quindi per la conservazione dell'energia meccanica
$Mlg=1/6Ml^2\omega_i^2+Mgl/2$ da cui $\omega_i=sqrt(3g/l)$
se l'urto è elastico si conservano sia l'energia cinetica che il momento angolare
chiamando $I$ il momento angolare dell'asta
$\{(1/2I\omega^2+1/2mv^2=0),(I\omega_i=mrv+I\omega):}$
$\{(1/6Ml^2\omega^2+1/2mv^2=0),(1/3Ml^2\omega_i=mrv+1/3Ml^2\omega):}$
da cui, saltanto tutti i passaggi
${(\omega=(Ml^2\omega_i)/(3r^2+Ml^2)+-sqrt((Ml^2\omega_i)/(r^2+1/3Ml^2))),(v=1/3Ml^2(\omega_i-\omega)/(mr)):}$
se l'urto è totalmente anelastico si conserva solo il momento angolare, dopo l'urto la sfera e l'asta si muovono come un unico corpo e la sfera ruota attorno all'ipotenusa del triangolo che ha per cateti il raggio della sfera e l'asta.
chiamando $I_s$ il momento di inerzia della sfera
$1/3Ml^2\omega_i=(I+I_s)\omega_f$
$1/3Ml^2\omega_i={1/3Ml^2+[2/5mr^2+(l^2+r^2)m]}\omega_f$
da cui $\omega_f=(Ml^2\omega_i)/(3[(1/3M+m)l^2+7/5mr^2])$
"giuliofis":
Non ce la faccio però a stare troppo dietro al forum in questi giorni.
ok, allora ti ringrazio per tutto il tempo che hai speso con il mio esercizio
"navigatore":
Ho trovato questa esauriente dispensa sul web, che parla di rotolamento e strisciamento in termini rigorosamente matematici. Conosco l'autore, è uno in gamba.
ti ringrazio tanto, me la studierò come si deve

"navigatore":
Ma più ci penso, e più penso che questo esercizio è quanto meno impreciso, secondo me...
e sapere che l'esercizio è preso da un compito d'esame fa davvero molto piacere...
](/datas/uploads/forum/emoji/eusa_wall.gif)


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo