Integrale con i residui e tangente

[xmaionx33]

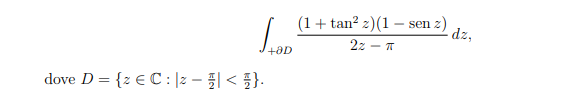
Ciao ragazzi , sto trovando difficoltà con questo esercizio non riesco a capire perchè pi/2 sia polo semplice e come si arriva a calcolare il residuo, la parte chi mi blocca è quella con la tangente non so proprio come trattarla, mi trovo che per il denominatore abbiamo in z=pi/2 un polo semplice e per (1-senz) z=pi/2 è uno zero di ordine 2 , ora come devo procedere con la tangente ?
questa la soluzione di wolfram:


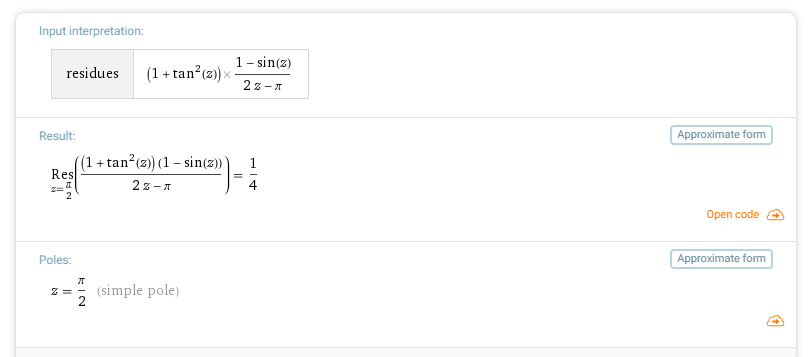
anche provando con pi/2 come polo semplice ( anche se non ho capito come si arriva) non capisco neanche come arriva a calcolarsi il residuo... grazie a chiunque riesca a farmelo capire , che ci sto sbattendo la testa da giorni

[Studente Anonimo]

Vale il seguente teorema:

Ipotesi

$lim_(z->z_0)(z-z_0)*f(z)=l ne 0$

Tesi

$[z=z_0]$ polo di ordine $1$ e residuo $l$

In questo caso:

$lim_(z->\pi/2)(z-\pi/2)*((1+tg^2z)(1-sinz))/(2z-\pi)=lim_(z->\pi/2)(z-\pi/2)*((1+sin^2z/cos^2z)(1-sinz))/(2(z-\pi/2))=$

$=lim_(z->\pi/2)(1-sinz)/(2cos^2z)=lim_(z->\pi/2)(1-sinz)/(2(1-sin^2z))=lim_(z->\pi/2)(1-sinz)/(2(1+sinz)(1-sinz))=lim_(z->\pi/2)1/(2(1+sinz))=1/4$