Studio della funzione $ f(x) = \frac{(-1)^{\lfloor x \rfloor}}{1+x} $
Salve a tutti
[ot]Come state? [/ot]
[/ot]
Come da titolo, sono qui oggi per discutere e/o ricevere consiglio riguardo questa funzione "antipatica".
Ricordo che $ \lfloor x \rfloor = \max \{ n \in \mathbb{Z} | n \leq x \} $.
Il dominio naturale risulta essere:
\[
\mathcal{D} = \mathbb{R} - \{-1 \}
\]
Ora, per quanto ne concerne i limiti, sapendo che $ (-1)^{-x} = (-1)^{x} $, si ha che
\[
- \frac{1}{1+x} \leq \frac{(-1)^{\lfloor x \rfloor}}{1+x} \leq \frac{1}{1+x}
\]
Pertanto, nel calcolo dei limiti, posso sfruttare il teorema dei carabinieri e $ \pm \frac{1}{1+x} $:
\[
\lim_{x \to \pm \infty} - \frac{1}{1+x} = \lim_{x \to \pm \infty} \frac{1}{1+x} = 0
\]
(ciò si poteva vedere pure ad occhio: alla fine l'unica cosa che può fare il numeratore è cambiare segno...)
\[
\lim_{x \to -1} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \lim_{x \to -1} \frac{(-1)^{\lfloor -1 \rfloor}}{0} = -\infty
\]
Per quanto ne concerne il segno, invece, quest'ultimo è determinato non solo dal segno del numeratore, ma da quello del denominatore. A causa di \lfloor x \rfloor, la funzione cambia segno per $ x $ intere: nell'intervallo $ (-\infty, 0) $, $ f $ è positiva negli intervalli $ (dispari, pari) $ di $ x $, mentre nell'intervallo $ (0, +\infty) $ è positiva negli intervalli $ (pari, dispari) $ di $ x $.
Dunque, di continuità e derivabilità in tutti i punti del dominio a coordinate intere non se ne parla nemmeno. Invece, $ f $ è continua in tutto il resto di $ \mathbb{D} $ in quanto somma, rapporto e composizione di funzioni elementari.
Ora, tutto quello che ho detto fin'ora sono intuizioni, che però non riesco a descrivere in matematichese. Naturalmente il Prof. non ci ha lasciato uno straccio di prova scritta o delucidazione in merito, e francamente mi aspetto anche che volesse solo due righe scritte.
Ma come dicono @pilloeffe e @gugo82, forse è meglio non fidarsi delle sole parole (i conti parlano).
Potete darmi una mano a mettere queste idee in chiaro?
P.S.: ecco un grafico di $ f $.
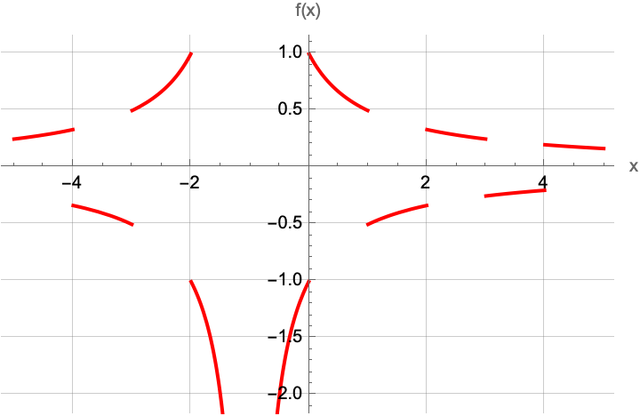
[ot]Come state?
Come da titolo, sono qui oggi per discutere e/o ricevere consiglio riguardo questa funzione "antipatica".
Ricordo che $ \lfloor x \rfloor = \max \{ n \in \mathbb{Z} | n \leq x \} $.
Il dominio naturale risulta essere:
\[
\mathcal{D} = \mathbb{R} - \{-1 \}
\]
Ora, per quanto ne concerne i limiti, sapendo che $ (-1)^{-x} = (-1)^{x} $, si ha che
\[
- \frac{1}{1+x} \leq \frac{(-1)^{\lfloor x \rfloor}}{1+x} \leq \frac{1}{1+x}
\]
Pertanto, nel calcolo dei limiti, posso sfruttare il teorema dei carabinieri e $ \pm \frac{1}{1+x} $:
\[
\lim_{x \to \pm \infty} - \frac{1}{1+x} = \lim_{x \to \pm \infty} \frac{1}{1+x} = 0
\]
(ciò si poteva vedere pure ad occhio: alla fine l'unica cosa che può fare il numeratore è cambiare segno...)
\[
\lim_{x \to -1} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \lim_{x \to -1} \frac{(-1)^{\lfloor -1 \rfloor}}{0} = -\infty
\]
Per quanto ne concerne il segno, invece, quest'ultimo è determinato non solo dal segno del numeratore, ma da quello del denominatore. A causa di \lfloor x \rfloor, la funzione cambia segno per $ x $ intere: nell'intervallo $ (-\infty, 0) $, $ f $ è positiva negli intervalli $ (dispari, pari) $ di $ x $, mentre nell'intervallo $ (0, +\infty) $ è positiva negli intervalli $ (pari, dispari) $ di $ x $.
Dunque, di continuità e derivabilità in tutti i punti del dominio a coordinate intere non se ne parla nemmeno. Invece, $ f $ è continua in tutto il resto di $ \mathbb{D} $ in quanto somma, rapporto e composizione di funzioni elementari.
Ora, tutto quello che ho detto fin'ora sono intuizioni, che però non riesco a descrivere in matematichese. Naturalmente il Prof. non ci ha lasciato uno straccio di prova scritta o delucidazione in merito, e francamente mi aspetto anche che volesse solo due righe scritte.
Ma come dicono @pilloeffe e @gugo82, forse è meglio non fidarsi delle sole parole (i conti parlano).
Potete darmi una mano a mettere queste idee in chiaro?
P.S.: ecco un grafico di $ f $.

Risposte
"ncant":
sapendo che $ (-1)^{-x} = (-1)^{x} $
Occhio che, quando \(x \in \mathbb{R} \setminus \mathbb{Z}\), \((-1)^x \) non è definita quando si studia analisi reale. Che significa \( (-1)^\sqrt{2} \)? Quindi, quella discussione si può fare come segue. Dato che per ogni \(x\in D\) risulta \(\lfloor x \rfloor \in \mathbb{Z} \) e quindi risulta \((-1)^{\lfloor x \rfloor} \in \{-1,1\} \), si ha: \[
0 \le \left|\frac{(-1)^{\lfloor x \rfloor}}{1+x}\right| = \frac{1}{|1+x|}
\]Il membro di destra tende a \(0\) per \(x \to \pm \infty\).
"ncant":
\[
\lim_{x \to -1} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \lim_{x \to -1} \frac{(-1)^{\lfloor -1 \rfloor}}{0} = -\infty
\]
A parte che c'è un errore di battitura (sostituisci e lasci la scrittura di limite), il valore del limite è giusto ma il procedimento per ottenerlo è logicamente sbagliato. Successivamente affermi correttamente che la funzione non è continua sugli interi, ma allora come ti permetti di sostituire alla funzione il valore su un intero per calcolarne il limite, che è proprio la definizione di continuità in quel punto intero? Riprova, distinguendo limite destro e sinistro e notando ad esempio che, se \(x \to -1^+\), allora puoi assumere \(-1 < x < 0 \) e quindi dedurre che \(\lfloor x \rfloor = -1\).
Il resto sul segno e sulla continuità/derivabilità lo puoi formalizzare considerando l'intervallo \([k,k+1)\) con \(k\in\mathbb{Z}\) arbitrario ed esplicitando il valore della funzione parte intera inferiore come ho fatto vedere nella discussione del limite: per ogni \(k \in \mathbb{Z}\), se \(k \le x < k+1\) allora \(\lfloor x \rfloor = k \).
Ultima nota: il grafico di \(f\), non un grafico di \(f\). Mica ce ne sono tanti
 .
.
Sorry per la grammatica, il copia incolla e gli orrori concettuali 
Quindi, se $ x \to -1^- $, posso assumere $ -2 < x < -1 $ e quindi dedurre che \( \lfloor x \rfloor = -2 \) ? E al quel punto posso scrivere:
\[
\lim_{x \to -1^-} f(x) = \lim_{x \to 1^-} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^2}{1-1} = -\infty
\]
\[
\lim_{x \to -1^+} f(x) = \lim_{x \to 1^+} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^{-1}}{1-1} = -\infty
\]
Spero di averci azzeccato...

"Mephlip":
Riprova, distinguendo limite destro e sinistro e notando ad esempio che, se \( x \to -1^+ \), allora puoi assumere \( -1 < x < 0 \) e quindi dedurre che \( \lfloor x \rfloor = -1 \).
Quindi, se $ x \to -1^- $, posso assumere $ -2 < x < -1 $ e quindi dedurre che \( \lfloor x \rfloor = -2 \) ? E al quel punto posso scrivere:
\[
\lim_{x \to -1^-} f(x) = \lim_{x \to 1^-} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^2}{1-1} = -\infty
\]
\[
\lim_{x \to -1^+} f(x) = \lim_{x \to 1^+} \frac{(-1)^{\lfloor x \rfloor}}{1+x} = \frac{(-1)^{-1}}{1-1} = -\infty
\]
Spero di averci azzeccato...
Esatto, a parte l'errore di battitura nell'ultimo limite da te scritto (dovrebbe essere \(x \to -1^+\)). A questo punto, se proprio vuoi scrivere \(1-1\), scrivi rispettivamente \(1-1^{-1}=0^-\) e \(1-1^+=0^+\) così si capisce come mai i limiti sono \(-\infty\)  .
.
Se vuoi conferme sul resto, scrivi pure e lo correggiamo.
 .
.Se vuoi conferme sul resto, scrivi pure e lo correggiamo.
"Mephlip":
Esatto, a parte l'errore di battitura nell'ultimo limite da te scritto
Oh mamma. Oggi sono peggio del mio prof quando scrive i quesiti/risposte dei compiti scritti...
"Mephlip":
Se vuoi conferme sul resto, scrivi pure e lo correggiamo.
Ok, grazie
Ora, se provo ad applicare lo stesso ragionamento per una qualsiasi $ x $ intera, dovrei anche essere in grado di verificare tutte le altre, vero?
Volessi proprio scegliere una qualsiasi $ k $ arbitraria:
\[
\lim_{x \to 2^-} f(x) = \frac{(-1)^1}{1+2} = - \frac{1}{3}; \qquad \lim_{x \to 2^+} f(x) = \frac{(-1)^2}{1+2} = \frac{1}{3}
\]
Non so però se è possibile trascrivere il segno di $ f $ in un'espressione, dato che prima l'ho detta a parole... Non penso che posso scrivere "pari" e "dispari".
Prego! Ragiona in generale. Considera \(k\in\mathbb{Z}\) arbitrario fissato e calcola:\[
\lim_{x \to k^+} f(x) \\
\lim_{x \to k^-} f(x)
\]Distinguendo \(k\) pari o \(k\) dispari. Fatto ciò, per l'arbitrarietà di \(k\in\mathbb{Z}\), hai il risultato su ogni intero.
\lim_{x \to k^+} f(x) \\
\lim_{x \to k^-} f(x)
\]Distinguendo \(k\) pari o \(k\) dispari. Fatto ciò, per l'arbitrarietà di \(k\in\mathbb{Z}\), hai il risultato su ogni intero.
Notazione strana, ma
\[
\lim_{x \to k_{\text{dispari}}^-} f(x) = \frac{(-1)^{k_{\text{dispari}} - 1}}{1 + k_{\text{dispari}}} = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{dispari}}} = \frac{1}{1 + k_{\text{dispari}}}; \;
\lim_{x \to k_{\text{dispari}}^+} f(x) = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{dispari}}} = - \frac{1}{1 + k_{\text{dispari}}}
\]
\[
\lim_{x \to k_{\text{pari}}^-} f(x) = \frac{(-1)^{k_{\text{pari}} - 1}}{1 + k_{\text{pari}}} = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{pari}}} = - \frac{1}{1 + k_{\text{pari}}}; \qquad
\lim_{x \to k_{\text{pari}}^+} f(x) = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{pari}}} = \frac{1}{1 + k_{\text{pari}}}
\]
\[
\lim_{x \to k_{\text{dispari}}^-} f(x) = \frac{(-1)^{k_{\text{dispari}} - 1}}{1 + k_{\text{dispari}}} = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{dispari}}} = \frac{1}{1 + k_{\text{dispari}}}; \;
\lim_{x \to k_{\text{dispari}}^+} f(x) = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{dispari}}} = - \frac{1}{1 + k_{\text{dispari}}}
\]
\[
\lim_{x \to k_{\text{pari}}^-} f(x) = \frac{(-1)^{k_{\text{pari}} - 1}}{1 + k_{\text{pari}}} = \frac{(-1)^{k_{\text{dispari}}}}{1 + k_{\text{pari}}} = - \frac{1}{1 + k_{\text{pari}}}; \qquad
\lim_{x \to k_{\text{pari}}^+} f(x) = \frac{(-1)^{k_{\text{pari}}}}{1 + k_{\text{pari}}} = \frac{1}{1 + k_{\text{pari}}}
\]
Sì, puoi anche alleggerire la notazione scrivendo \(k_{\text{p}}\) e \(k_{\text{d}}\). Dunque, cosa deduci da ciò?
E per la derivabilità? Sappiamo che la parte intera inferiore non è derivabile sugli interi perché, con lo stesso approccio del tuo ultimo messaggio, non è continua. Come dimostri la derivabilità della funzione parte intera inferiore in \(\mathbb{R}\setminus\mathbb{Z}\)?
E per la derivabilità? Sappiamo che la parte intera inferiore non è derivabile sugli interi perché, con lo stesso approccio del tuo ultimo messaggio, non è continua. Come dimostri la derivabilità della funzione parte intera inferiore in \(\mathbb{R}\setminus\mathbb{Z}\)?
Deduco che $ f $ non è di certo né continua né derivabile in tutti i punti del dominio a coordinate intere. Però è continua altrove (eccetto dove escluso dal dominio naturale), dato che, mentre $ \lfloor x \rfloor $ può restituire solo valori interi (per quanto da te affermato penso nel primo messaggio), il denominatore di $ f $ comunque lavora sui reali, dunque "c'è sempre una piccola variazione di$ f (x) $ quando $ x $ varia di poco" (o almeno, così dice il mio Prof, poi se è possibile formalizzarlo ancora di più, sarebbe molto meglio...).
Potrei rappresentare $ \lfloor x \rfloor $ come una serie
[asvg]xmin=-3;xmax=3;ymin=-3;ymax=3;
axes("");
stroke="red";
plot("0",0,1); plot("1",1,2);plot("2",2,3);plot("3",3,4);plot("-1",-1,0);plot("-2",-2,-1);plot("-3",-3,-2);plot("-4",-4,-3);[/asvg]
\[
\lfloor x \rfloor =\sum_{n=-\infty}^{+\infty} n\ [\text{u}(t-n)-\text{u}(t-n-1) ]
\]
(in cui [tex]$\text{u}(t)$[/tex] è il gradino unitario)
Ma lo trovo davvero poco intuitivo nel mio caso (poi boh...)
Mi verrebbe da dire che $ \lfloor x \rfloor $ abbia derivata prima nulla $ \forall x \in \mathbb{R} $, dato che in realtà la sua legge è quella serie.
Comunque la derivata di $ f $ è garantita (dove possibile, cioè non nelle coordinate intere e in $ x = -1 $) da teoremi analoghi a quelli delle funzioni continue che coinvolgono la somma, prodotto, composizione... di funzioni continue (tanto \lfloor x \rfloor restituisce solo valori interi...)
Potrei rappresentare $ \lfloor x \rfloor $ come una serie
[asvg]xmin=-3;xmax=3;ymin=-3;ymax=3;
axes("");
stroke="red";
plot("0",0,1); plot("1",1,2);plot("2",2,3);plot("3",3,4);plot("-1",-1,0);plot("-2",-2,-1);plot("-3",-3,-2);plot("-4",-4,-3);[/asvg]
\[
\lfloor x \rfloor =\sum_{n=-\infty}^{+\infty} n\ [\text{u}(t-n)-\text{u}(t-n-1) ]
\]
(in cui [tex]$\text{u}(t)$[/tex] è il gradino unitario)
Ma lo trovo davvero poco intuitivo nel mio caso (poi boh...)
Mi verrebbe da dire che $ \lfloor x \rfloor $ abbia derivata prima nulla $ \forall x \in \mathbb{R} $, dato che in realtà la sua legge è quella serie.
Comunque la derivata di $ f $ è garantita (dove possibile, cioè non nelle coordinate intere e in $ x = -1 $) da teoremi analoghi a quelli delle funzioni continue che coinvolgono la somma, prodotto, composizione... di funzioni continue (tanto \lfloor x \rfloor restituisce solo valori interi...)
Niente serie direi. Il punto è che non so/non ricordo se hai già dimostrato che \(\lfloor x \rfloor \) è continua in \(\mathbb{R}\setminus\mathbb{Z}\). Perché, se non lo hai fatto, non puoi usare i teoremi di regolarità per dedurre la continuità di \(f\), in quanto appunto non sai se il numeratore è continuo o no. Prova a dimostrarlo ora.
Stesso problema per la derivabilità: il ragionamento va bene, ma hai dimostrato che \(\lfloor x \rfloor\) è derivabile in \(\mathbb{R}\setminus\mathbb{Z}\)? Se no, prova a farlo ora.
Stesso problema per la derivabilità: il ragionamento va bene, ma hai dimostrato che \(\lfloor x \rfloor\) è derivabile in \(\mathbb{R}\setminus\mathbb{Z}\)? Se no, prova a farlo ora.
[ot]"Golden Sneer" parte in sottofondo.[/ot]
Sia $ k \in \mathbb{Z} $ e $ m \in (k, k + 1) $, si ha:
\[
\lim_{x \to m^+} ⌊x⌋ = \lim_{x \to m^-} ⌊x⌋ = ⌊m⌋
\]
(Es.: $ ⌊1,2⌋ = 1; ⌊1,19⌋ = 1; ⌊1,21⌋ = 1 $)
Sia $ k \in \mathbb{Z} $ e $ m \in (k, k + 1) $, si ha:
\[
\lim_{x \to m^+} ⌊x⌋ = \lim_{x \to m^-} ⌊x⌋ = ⌊m⌋
\]
(Es.: $ ⌊1,2⌋ = 1; ⌊1,19⌋ = 1; ⌊1,21⌋ = 1 $)
Sì, è vero, ma perché è vero? Devi usare un argomento \(\varepsilon\)-\(\delta_{\varepsilon}\) per dimostrarlo (o, eventualmente, teoremi). Altrimenti potrei contestare che sei andato a intuito con gli esempi o hai semplicemente sostituito.
Ci provo:
Sia $ n \in \mathbb{Z} $. Allora $ \lfloor n \rfloor = n$. Considerando invece $ x \in \mathbb{R} $, ne risulta che $ \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1 $.
Consideriamo l'intervallo aperto $ (n, n+1) $. Si ha:
\[ \forall x \in (n, n+1) : \lfloor x \rfloor = n \]
Ciò risulta in
\[ \forall x \in (n, n+1) : \lfloor x \rfloor - n = 0
\]
Ora, sia $ \varepsilon \in \mathbb{R}_{> 0} $ e sia $ \delta \in (n, n+1) $. Allora:
\[ \forall x \in (n, n+1) : n < x < n + \delta : \left| \lfloor x \rfloor - n \right| < \varepsilon \]
Cioè
\[
\lim_{x \to n^+} \lfloor x \rfloor = \lfloor n \rfloor = n
\]
Sia $ n \in \mathbb{Z} $. Allora $ \lfloor n \rfloor = n$. Considerando invece $ x \in \mathbb{R} $, ne risulta che $ \lfloor x \rfloor \leq x < \lfloor x \rfloor + 1 $.
Consideriamo l'intervallo aperto $ (n, n+1) $. Si ha:
\[ \forall x \in (n, n+1) : \lfloor x \rfloor = n \]
Ciò risulta in
\[ \forall x \in (n, n+1) : \lfloor x \rfloor - n = 0
\]
Ora, sia $ \varepsilon \in \mathbb{R}_{> 0} $ e sia $ \delta \in (n, n+1) $. Allora:
\[ \forall x \in (n, n+1) : n < x < n + \delta : \left| \lfloor x \rfloor - n \right| < \varepsilon \]
Cioè
\[
\lim_{x \to n^+} \lfloor x \rfloor = \lfloor n \rfloor = n
\]
Non abbiamo detto che la parte intera inferiore è discontinua sugli interi? Perché stai cercando di dimostrare la continuità su un intero generico? O vuoi fare altro e non ti sto seguendo?
Devi dimostrare la continuità in un arbitrario \(x_0 \in \mathbb{R}\setminus\mathbb{Z}\). L'idea che hai avuto nell'ultimo messaggio non è male, prova a riciclarla osservando che:\[
\mathbb{R}\setminus\mathbb{Z}\ = \bigcup_{k\in\mathbb{Z}} (k,k+1)
\]
Devi dimostrare la continuità in un arbitrario \(x_0 \in \mathbb{R}\setminus\mathbb{Z}\). L'idea che hai avuto nell'ultimo messaggio non è male, prova a riciclarla osservando che:\[
\mathbb{R}\setminus\mathbb{Z}\ = \bigcup_{k\in\mathbb{Z}} (k,k+1)
\]
"Mephlip":
Non abbiamo detto che la parte intera inferiore è discontinua sugli interi? Perché stai cercando di dimostrare la continuità su un intero generico? O vuoi fare altro e non ti sto seguendo?
https://proofwiki.org/wiki/Floor_Functi ... at_Integer
Un procedimento simile viene fatto qui. (pp. 5-6)
"Mephlip":
Devi dimostrare la continuità in un arbitrario \(x_0 \in \mathbb{R}\setminus\mathbb{Z}\). L'idea che hai avuto nell'ultimo messaggio non è male, prova a riciclarla osservando che:\[
\mathbb{R}\setminus\mathbb{Z}\ = \bigcup_{k\in\mathbb{Z}} (k,k+1)
\]
Una parola allora... dammi un po' di tempo e modifico questo messaggio.
Ma quella da te linkata è la continuità a destra. Una funzione è continua se e solo se è continua a destra e a sinistra; infatti, se fai lo stesso ragionamento a sinistra non funziona. Per farlo funzionare, devi considerare \(n-1\) anziché \(n\), quindi non è continua perché sono diversi i risultati che ottieni a destra e sinistra. Hai anche postato il grafico, è discontinua sugli interi.
Si consideri $ f(x) = \lfloor a \rfloor $.
Sia $ a \notin \mathbb{Z} $. Considerando $ \varepsilon > 0 $, sia $ \delta = \min \{ a - \lfloor a \rfloor, \lfloor a + 1 \rfloor - a \} $. Dato che $ a \notin \mathbb{Z} $, allora $ a \ne \lfloor a \rfloor $ e $ a \ne \lfloor a + 1 \rfloor $. Dunque, $ \delta > 0 $. Si noti che per tutte $ x $ che soddisfano $ | x - a | < \delta $, si ha che
\[
f(x) = \lfloor x \rfloor = \lfloor a \rfloor.
\]
Pertanto:
\[
| f(x) - f(a) | = | f(a) - f(a) | = 0 < \varepsilon
\]
da cui (si spera) si deduce che $ f $ è continua in $ a $.
Sia $ a \notin \mathbb{Z} $. Considerando $ \varepsilon > 0 $, sia $ \delta = \min \{ a - \lfloor a \rfloor, \lfloor a + 1 \rfloor - a \} $. Dato che $ a \notin \mathbb{Z} $, allora $ a \ne \lfloor a \rfloor $ e $ a \ne \lfloor a + 1 \rfloor $. Dunque, $ \delta > 0 $. Si noti che per tutte $ x $ che soddisfano $ | x - a | < \delta $, si ha che
\[
f(x) = \lfloor x \rfloor = \lfloor a \rfloor.
\]
Pertanto:
\[
| f(x) - f(a) | = | f(a) - f(a) | = 0 < \varepsilon
\]
da cui (si spera) si deduce che $ f $ è continua in $ a $.
Sì, va bene. L'idea intuitiva è sostanzialmente la seguente: essendo \(x_0 \notin\mathbb{Z}\) "c'è spazio" tra \(x_0\) e due interi consecutivi. Quindi, dato che \(x \to x_0\), a patto di restringere opportunamente la distanza tra \(x\) e \(x_0\) (ossia, a patto di prendere \(\delta_{\varepsilon}\) sufficientemente piccolo), si riesce a inserire \(x\) e \(x_0\) tra due interi consecutivi e dunque a far sì che abbiano la stessa parte intera inferiore (o superiore, infatti la dimostrazione per la parte intera superiore è identica). L'ipotesi che \(x_0 \notin\mathbb{Z}\) è fondamentale, perché altrimenti non importa quanto si riduca la distanza tra \(x\) e \(x_0\): non si riesce a metterli entrambi tra due interi consecutivi.
Per la derivabilità in \(\mathbb{R}\setminus\mathbb{Z}\)?
Per la derivabilità in \(\mathbb{R}\setminus\mathbb{Z}\)?
[ot]Ahhhhh... ho capito. Questo è il test d'ingresso per diventare un membro di Bourbaki 
(si scherza, gente!)[/ot]

(si scherza, gente!)[/ot]
[ot] In effetti, queste cose le prime volte che si vedono formalizzate sembrano roba aliena. Ma poi ci si fa l'abitudine.[/ot]
In effetti, queste cose le prime volte che si vedono formalizzate sembrano roba aliena. Ma poi ci si fa l'abitudine.[/ot]
 In effetti, queste cose le prime volte che si vedono formalizzate sembrano roba aliena. Ma poi ci si fa l'abitudine.[/ot]
In effetti, queste cose le prime volte che si vedono formalizzate sembrano roba aliena. Ma poi ci si fa l'abitudine.[/ot]
Sento che dovrei usare la solita formula per la derivabilità ma usando un generico $ x_0 \ne \mathbb{Z} $, ma mi sfugge...
Posso comprare una vocale?
Posso comprare una vocale?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo