Soluzione del limite...
Mi è capito un limite piuttosto strano nel senso che non so come risolverlo, non si può usare taylor e non credo nemmeno si possa fare niente con i limiti notevoli...
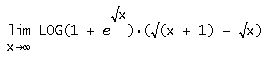
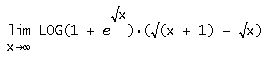
Risposte
Io ho provato a farlo calcolare a Derive, ma non mi
dà un risultato numerico: mi dice solo che calcolare
questo limite equivale a calcolare:

dà un risultato numerico: mi dice solo che calcolare
questo limite equivale a calcolare:

Non puoi usare Taylor perché il testo te lo impedisce o perché tu credi che non sia utile? Nel secondo caso invece...:
sqrt(x+1)-sqrt(x) = sqrt(x) * [ sqrt(1+1/x) - 1 ] =
e ora uso taylor al prim'ordine:
= sqrt(x) * [ 1 + 1/(2x) - 1 ] + ... = sqrt(x)/2x + ... = 1/(2*sqrt(x)) + ...
e ora il limite è semplice.
[con l'esponenziale ti puoi comportare nello stesso modo]
sqrt(x+1)-sqrt(x) = sqrt(x) * [ sqrt(1+1/x) - 1 ] =
e ora uso taylor al prim'ordine:
= sqrt(x) * [ 1 + 1/(2x) - 1 ] + ... = sqrt(x)/2x + ... = 1/(2*sqrt(x)) + ...
e ora il limite è semplice.
[con l'esponenziale ti puoi comportare nello stesso modo]
Come risultato ho
lim x-->inf. = 1/{2*[ln(2)+ln(5)]}
lim x-->inf. = 0,2171472409516259138255644594583
Ciao, Ermanno
lim x-->inf. = 1/{2*[ln(2)+ln(5)]}
lim x-->inf. = 0,2171472409516259138255644594583
Ciao, Ermanno
io dicevo che non si può usare taylor, perchè il limite non era tendente a zero, e quindi non sapevo come centrarlo... cioè mi spiegate come mai poi esce tendente a zero ?
...sqrt(x) * [ sqrt(1+1/x) - 1 ]...
1/x tende a 0 se x tende a infinito. Quindi posso espandere in serie di taylor sqrt(1+1/x). Ovvero, prendi la funzione sqrt(1+y) ed espandila in serie di taylor, poi sostituisci y=1/x.
1/x tende a 0 se x tende a infinito. Quindi posso espandere in serie di taylor sqrt(1+1/x). Ovvero, prendi la funzione sqrt(1+y) ed espandila in serie di taylor, poi sostituisci y=1/x.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo