Integrale improprio con Teorema dei residui
\[ \int_{\gamma_1} f(z) dz + \int_{\gamma_3} f(z) dz = (1- e^{2a \pi i}) \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx \]Salve a tutti, sto cercando invano di venire a capo di questo integrale:
$$
\int_{-\infty}^{+\infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx
\;\;\;\,\,\,\,\,\,\,
a \in (0,2)
$$
Cerco di calcolarlo col Teorema dei residui, sembrandomi convergente, per i valori detti di $a$ .
Allora considero la funzione complessa:
$$
f(z) = \frac{e^{az}}{e^{2z} - e^z +1}
$$
e la integro sulla frontiera del rettangolo
$$
D = \{ z \in \mathbb{C} \,\,\, t.c. \,\,\, -R \leq Re(z) \leq +R , \,\,\, 0 \leq Im(z) \leq 2\pi \}
$$
L'unico polo della funzione, appartenente a D, mi sembra essere $z = e^{i \frac{\pi}{3}}$ .
E' un polo del primo ordine e ne calcolo il residuo:
$$
Res(f ; e^{i \frac{\pi}{3}}) = \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) }
$$
Ora studio l'integrale complesso.
$$
\int_{+ \partial D} f(z) dz =
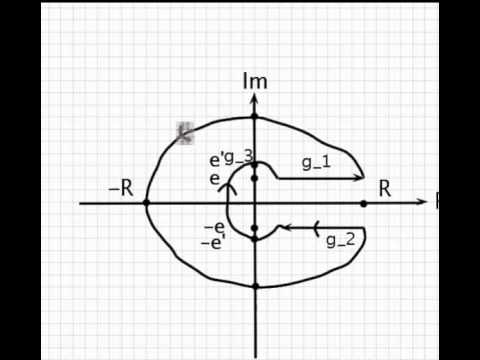
\int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz + \int_{\gamma_3} f(z) dz + \int_{\gamma_4} f(z) dz = \\
\int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx +
\int_0^{2\pi} \frac{e^{a(R+it)}}{e^{2(R+it)} - e^{R+it} +1} dt +
\int_{-R}^{+R} \frac{e^{a(x+2\pi i)}}{e^{2(x+2\pi i)} - e^{x+2\pi i} +1} dx -
\int_0^{2\pi} \frac{e^{a(-R+it)}}{e^{2(-R+it)} - e^{-R+it} +1} dt +
$$
Chiamando $X = \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx$ e tenendo presente che $e^{2k \pi i} = 1$ per $\k \in \mathbb{Z}$ , si ha che:
$$
\int_{-R}^{+R} \frac{e^{a(x+2\pi i)}}{e^{2(x+2\pi i)} - e^{x+2\pi i} +1} dx \,\, = \,\, -(e^{2a \pi i}) \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
Quindi si ha:
$$
\int_{\gamma_1} f(z) dz + \int_{\gamma_3} f(z) dz = (1- e^{2a \pi i}) \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
Utilizzando le disuguaglianze triangolari e altri trucchetti si dimostra che, per $R \rightarrow + \infty$ si ha:
$$
\int_{\gamma_2} f(z) dz = \int_{\gamma_4} f(z) dz = 0
$$
Per il teorema dei residui abbiamo
$$
2 \pi i \,\,Res(f ; e^{i \frac{\pi}{3}}) = \int_{+ \partial D} f(z) dz =
\int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz + \int_{\gamma_3} f(z) dz + \int_{\gamma_4} f(z) dz
$$
Al tendere di $R$ a $+ \infty$ si ha, dunque:
$$
2 \pi i \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) } =
(1- e^{2a \pi i}) \int_{- \infty}^{+ \infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
E qui incominciano i problemi:
1) per $a=1$ , essendo sempre $e^{2k \pi i} = 1$ , per $\k \in \mathbb{Z}$, il secondo membro dell'ultima uguaglianza sarebbe nullo, e ciò contrasta col primo membro, che sarebbe uguale a $ \pi 2 / \sqrt{3}$ !
2) Anche tralasciando questo primo problema, per gli altri valori di $a$ si ha che
$$
I = \int_{- \infty}^{+ \infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx = 2 \pi i \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) (1- e^{2a \pi i}) }
$$
che, facendo i conti, non è reale per ogni valore di $a$.
Dove sbaglio?
$$
\int_{-\infty}^{+\infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx
\;\;\;\,\,\,\,\,\,\,
a \in (0,2)
$$
Cerco di calcolarlo col Teorema dei residui, sembrandomi convergente, per i valori detti di $a$ .
Allora considero la funzione complessa:
$$
f(z) = \frac{e^{az}}{e^{2z} - e^z +1}
$$
e la integro sulla frontiera del rettangolo
$$
D = \{ z \in \mathbb{C} \,\,\, t.c. \,\,\, -R \leq Re(z) \leq +R , \,\,\, 0 \leq Im(z) \leq 2\pi \}
$$
L'unico polo della funzione, appartenente a D, mi sembra essere $z = e^{i \frac{\pi}{3}}$ .
E' un polo del primo ordine e ne calcolo il residuo:
$$
Res(f ; e^{i \frac{\pi}{3}}) = \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) }
$$
Ora studio l'integrale complesso.
$$
\int_{+ \partial D} f(z) dz =
\int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz + \int_{\gamma_3} f(z) dz + \int_{\gamma_4} f(z) dz = \\
\int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx +
\int_0^{2\pi} \frac{e^{a(R+it)}}{e^{2(R+it)} - e^{R+it} +1} dt +
\int_{-R}^{+R} \frac{e^{a(x+2\pi i)}}{e^{2(x+2\pi i)} - e^{x+2\pi i} +1} dx -
\int_0^{2\pi} \frac{e^{a(-R+it)}}{e^{2(-R+it)} - e^{-R+it} +1} dt +
$$
Chiamando $X = \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx$ e tenendo presente che $e^{2k \pi i} = 1$ per $\k \in \mathbb{Z}$ , si ha che:
$$
\int_{-R}^{+R} \frac{e^{a(x+2\pi i)}}{e^{2(x+2\pi i)} - e^{x+2\pi i} +1} dx \,\, = \,\, -(e^{2a \pi i}) \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
Quindi si ha:
$$
\int_{\gamma_1} f(z) dz + \int_{\gamma_3} f(z) dz = (1- e^{2a \pi i}) \int_{-R}^{+R} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
Utilizzando le disuguaglianze triangolari e altri trucchetti si dimostra che, per $R \rightarrow + \infty$ si ha:
$$
\int_{\gamma_2} f(z) dz = \int_{\gamma_4} f(z) dz = 0
$$
Per il teorema dei residui abbiamo
$$
2 \pi i \,\,Res(f ; e^{i \frac{\pi}{3}}) = \int_{+ \partial D} f(z) dz =
\int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz + \int_{\gamma_3} f(z) dz + \int_{\gamma_4} f(z) dz
$$
Al tendere di $R$ a $+ \infty$ si ha, dunque:
$$
2 \pi i \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) } =
(1- e^{2a \pi i}) \int_{- \infty}^{+ \infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx
$$
E qui incominciano i problemi:
1) per $a=1$ , essendo sempre $e^{2k \pi i} = 1$ , per $\k \in \mathbb{Z}$, il secondo membro dell'ultima uguaglianza sarebbe nullo, e ciò contrasta col primo membro, che sarebbe uguale a $ \pi 2 / \sqrt{3}$ !
2) Anche tralasciando questo primo problema, per gli altri valori di $a$ si ha che
$$
I = \int_{- \infty}^{+ \infty} \frac{e^{ax}}{e^{2x} - e^x +1} dx = 2 \pi i \frac{e^{ai\frac{\pi}{3}}}{e^{i \frac{\pi}{3}} ( e^{i \frac{\pi}{3}} - e^{-i \frac{\pi}{3}} ) (1- e^{2a \pi i}) }
$$
che, facendo i conti, non è reale per ogni valore di $a$.
Dove sbaglio?
Risposte
Non ho avuto il tempo di provare a fare il conto esplicito di tutto, ma ho notato che al denominatore hai
\[\frac{1}{e^{2x}-e^{x}+1} =\frac{1}{e^{x}(e^{x}+e^{-x}-1)}=\frac{1}{e^x(2\cosh{x}-1)}\]
quindi hai un polo sul cammino sull'asse reale per \(\cosh{x}=\frac{1}{2}\)
Ti consiglierei quindi di fare un taglio lungo l'asse reale e integrare con un percorso alla pacman
così eviti la singolarità, però trovi solo l'integrale tra \(0\) e \(\infty\), per l'altra parte basta fare un secondo integrale uguale solo con il taglio lungo l'asse negativo.
Domani che ho tempo prova a fare tutto l'esercizio comunque
\[\frac{1}{e^{2x}-e^{x}+1} =\frac{1}{e^{x}(e^{x}+e^{-x}-1)}=\frac{1}{e^x(2\cosh{x}-1)}\]
quindi hai un polo sul cammino sull'asse reale per \(\cosh{x}=\frac{1}{2}\)
Ti consiglierei quindi di fare un taglio lungo l'asse reale e integrare con un percorso alla pacman
così eviti la singolarità, però trovi solo l'integrale tra \(0\) e \(\infty\), per l'altra parte basta fare un secondo integrale uguale solo con il taglio lungo l'asse negativo.
Domani che ho tempo prova a fare tutto l'esercizio comunque
Ma il coseno iperbolico assume il suo valore minimo per $x = 0$ , e lì vale 1, quindi non può mai essere uguale ad $1/2$ .
Infatti hai ragione,scusa non ci avevo fatto caso subito, poi quando ho rifatto il conto con calma me ne sono accorto.
Facendo il conto con il lemma del grande cerchio si ottiene
\[I(a)=\int ... dx=2 \pi \frac{e^{(a-1)i \frac{\pi}{3}}}{\sqrt{3}}\]
Però per \(a=1\), sostituendo \(z=e^x\) trovi una primitiva e il risultato dovrebbe essere \(I(1)=\frac{2}{3}\frac{2\pi}{\sqrt{3}} \), quel \(\frac{2}{3}\) overall non compare però nel calcolo con il teorema dei residui.
Provo a fare in qualche altro modo, cambiando percorso magari
Facendo il conto con il lemma del grande cerchio si ottiene
\[I(a)=\int ... dx=2 \pi \frac{e^{(a-1)i \frac{\pi}{3}}}{\sqrt{3}}\]
Però per \(a=1\), sostituendo \(z=e^x\) trovi una primitiva e il risultato dovrebbe essere \(I(1)=\frac{2}{3}\frac{2\pi}{\sqrt{3}} \), quel \(\frac{2}{3}\) overall non compare però nel calcolo con il teorema dei residui.
Provo a fare in qualche altro modo, cambiando percorso magari
Ho effettuato la sostituzione $z=e^x$ e l'integrale divente da 0 a infinito, integarando su un cammino alla packman ottieni
$$I(a)=\frac{2 \pi}{\sqrt{3}} \frac{\sin(\frac{2}{3}(a-1)\pi)}{\sin((a-1)\pi)}$$
$$I(a)=\frac{2 \pi}{\sqrt{3}} \frac{\sin(\frac{2}{3}(a-1)\pi)}{\sin((a-1)\pi)}$$


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo