Integrale con valore assoluto
Salve ragazzi,
sto preparando l'esame di Analisi Matematica e purtroppo sono incappato in un integrale, del cui svolgimento il mio libro riporta direttamente un passaggio che non riesco a giustificare che è il seguente:
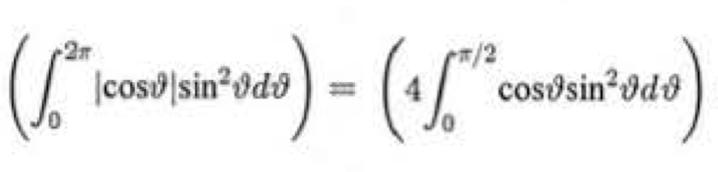
Nello specifico noto che elimina il valore assoluto dimezzando per ben due volte l'intervallo di integrazione, così da ritrovarsi nell'intervallo [0,pi/2] in cui il coseno è sicuramente positivo, tuttavia non mi è chiaro come arrivare a dimostrare che possa spezzare questo specifico integrali in 4 uguali sommabili, anche perché vedo quel sen^2 che mi complica ulteriormente la comprensione della cosa (come faccio a dire che ciò che sto facendo per il coseno sia valido anche per il seno)?
Grazie mille!
sto preparando l'esame di Analisi Matematica e purtroppo sono incappato in un integrale, del cui svolgimento il mio libro riporta direttamente un passaggio che non riesco a giustificare che è il seguente:
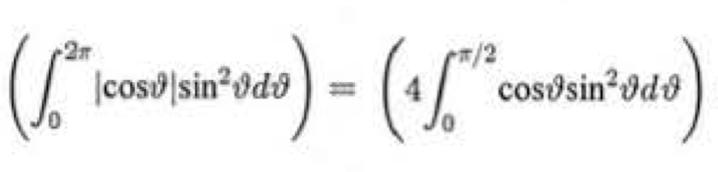
Nello specifico noto che elimina il valore assoluto dimezzando per ben due volte l'intervallo di integrazione, così da ritrovarsi nell'intervallo [0,pi/2] in cui il coseno è sicuramente positivo, tuttavia non mi è chiaro come arrivare a dimostrare che possa spezzare questo specifico integrali in 4 uguali sommabili, anche perché vedo quel sen^2 che mi complica ulteriormente la comprensione della cosa (come faccio a dire che ciò che sto facendo per il coseno sia valido anche per il seno)?
Grazie mille!
Risposte
Ciao Matheeus,
Capisco che sono i tuoi primi messaggi, ma dovresti cercare di evitare di postare foto ed invece scrivere le formule come prescritto dal regolamento. Stavolta te lo faccio io, con preghiera di modificare di conseguenza il tuo OP.
$(\int_0^{2\pi} |cos\theta| sin^2\theta \text{d}\theta) = (4 \int_0^{\pi/2} cos\theta sin^2\theta \text{d}\theta) $
Quanto alla questione che hai posto, spezzerei il primo integrale in $4$, cioè, omettendo per comodità la funzione integranda
$int_0^{2\pi} = \int_0^{\pi/2} + \int_{pi/2}^{\pi} + \int_{\pi}^{(3\pi)/2} + \int_{(3\pi)/2}^{2\pi} $
Con opportuni cambiamenti di variabile dovresti riuscire a dimostrare che gli ultimi 3 integrali sono uguali al primo considerando che per la definizione di modulo o valore assoluto si ha:
$|cos\theta| = {(cos\theta \text{ se } cos\theta \ge 0 \iff 0 \le \theta \le \pi/2 \vv (3\pi)/2 \le \theta < 2\pi),(- cos\theta \text{ se } cos\theta < 0 \iff \pi/2 < \theta \le \pi \vv \pi < \theta < (3\pi)/2):} $
Comunque il tuo libro ha ragione e si ha:
$(\int_0^{2\pi} |cos\theta| sin^2\theta \text{d}\theta) = (4 \int_0^{\pi/2} cos\theta sin^2\theta \text{d}\theta) = 4/3 $
Capisco che sono i tuoi primi messaggi, ma dovresti cercare di evitare di postare foto ed invece scrivere le formule come prescritto dal regolamento. Stavolta te lo faccio io, con preghiera di modificare di conseguenza il tuo OP.
$(\int_0^{2\pi} |cos\theta| sin^2\theta \text{d}\theta) = (4 \int_0^{\pi/2} cos\theta sin^2\theta \text{d}\theta) $
$(\int_0^{2\pi} |cos\theta| sin^2\theta \text{d}\theta) = (4 \int_0^{\pi/2} cos\theta sin^2\theta \text{d}\theta) $
Quanto alla questione che hai posto, spezzerei il primo integrale in $4$, cioè, omettendo per comodità la funzione integranda
$int_0^{2\pi} = \int_0^{\pi/2} + \int_{pi/2}^{\pi} + \int_{\pi}^{(3\pi)/2} + \int_{(3\pi)/2}^{2\pi} $
Con opportuni cambiamenti di variabile dovresti riuscire a dimostrare che gli ultimi 3 integrali sono uguali al primo considerando che per la definizione di modulo o valore assoluto si ha:
$|cos\theta| = {(cos\theta \text{ se } cos\theta \ge 0 \iff 0 \le \theta \le \pi/2 \vv (3\pi)/2 \le \theta < 2\pi),(- cos\theta \text{ se } cos\theta < 0 \iff \pi/2 < \theta \le \pi \vv \pi < \theta < (3\pi)/2):} $
Comunque il tuo libro ha ragione e si ha:
$(\int_0^{2\pi} |cos\theta| sin^2\theta \text{d}\theta) = (4 \int_0^{\pi/2} cos\theta sin^2\theta \text{d}\theta) = 4/3 $


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo