Esercizio: Convergenza integrali
Salve ragazzi, ho un problema che mi sta' facendo impazzire. Premetto che sono ormai un po' di anni che nn affronto problemi di matematica "pura", percui non tutti i concetti sono limpidi nella mia mente.
Oggi non sono riuscito a dimostrare che il seguente integrale converge:
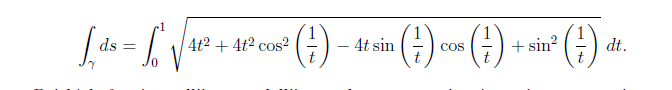
Devo dimostrare che il limite per x->0+ dell'integrale esiste ed è finito giusto?
Grazie
Oggi non sono riuscito a dimostrare che il seguente integrale converge:
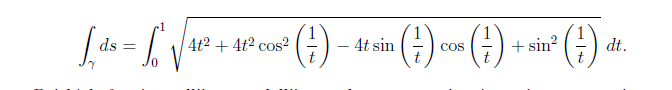
Devo dimostrare che il limite per x->0+ dell'integrale esiste ed è finito giusto?
Grazie
Risposte
Credo che se il problema sia la convergenza, si possa usare questo stratgemma qui sotto (t. Bernoulli)
[tex]\sqrt{4t^2+4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)} \leqslant \sqrt{4t^2}+\sqrt{4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)}[/tex]
[tex]\sqrt{4t^2+4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)} \leqslant 2t + \left [ 2t\ cos\left (\frac{1 }{t} \right )-sin\left (\frac{1 }{t} \right) \right ][/tex]
Rimpicciolisci i caratteri sennò la formula può uscire dallo schermo.
[tex]\sqrt{4t^2+4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)} \leqslant \sqrt{4t^2}+\sqrt{4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)}[/tex]
[tex]\sqrt{4t^2+4tcos^2\left (\frac{1 }{t} \right)-4t^2cos\left (\frac{1 }{t} \right)sin\left (\frac{1 }{t} \right)+sin^2\left (\frac{1 }{t} \right)} \leqslant 2t + \left [ 2t\ cos\left (\frac{1 }{t} \right )-sin\left (\frac{1 }{t} \right) \right ][/tex]
Rimpicciolisci i caratteri sennò la formula può uscire dallo schermo.
Quindi il tutto si riduce a vedere il limite della membro in basso. Ok, mi è abbastanza chiaro il ragionamento. Ma poi:
$ lim_(x -> 0+) 2t + sqrt(2tcos(1/t) - sin(1/t)) $
Come si risolve? Diciamo che il problema sono 1 po' i limiti, più che altro.
Grazie
$ lim_(x -> 0+) 2t + sqrt(2tcos(1/t) - sin(1/t)) $
Come si risolve? Diciamo che il problema sono 1 po' i limiti, più che altro.
Grazie
A me pare che tu debba dimostrare che la curva $ul(phi)(t)=(2t,2tcos(1/t)-sin(1/t))$, è/non è rettificabile.
E sinceramente io cercherei altre vie per farlo, piuttosto che pigliare l'integrale della lunghezza della curva e far vedere che è finito/infinito.
Ps: Quinzio quale disuguaglianza avresti usato per fare quelle maggiorazioni?
Pps: pensandoci bene è quasi ovvio che quella curva non sia rettificabile e che di conseguenza l'integrale non converga.
E sinceramente io cercherei altre vie per farlo, piuttosto che pigliare l'integrale della lunghezza della curva e far vedere che è finito/infinito.
Ps: Quinzio quale disuguaglianza avresti usato per fare quelle maggiorazioni?
Pps: pensandoci bene è quasi ovvio che quella curva non sia rettificabile e che di conseguenza l'integrale non converga.
Veramente la soluzione dice che la curva è rettificabile. Aspetta lo posto tutto:
E, una volta determinato ds, il ragionamento del prof è questo:
Come fa' a dire che la funzione è limitate per t->0+??
E, una volta determinato ds, il ragionamento del prof è questo:
Come fa' a dire che la funzione è limitate per t->0+??
Sì sono un idiota, non ho fatto la derivata della parametrizzazione -.-'
Comunque sì in teoria si fa anche così, che è limitata è vero perchè anche se l'integranda non ammette limite i suoi valori non superano una certa costante, quindi puoi utilizzare la monotonia dell'integrale come ha fatto il tuo professore e concludere che quell'integrale improprio converge (dal di sotto lo minori con lo $0$ perchè l'integranda è a segno costante positivo).
Comunque sì in teoria si fa anche così, che è limitata è vero perchè anche se l'integranda non ammette limite i suoi valori non superano una certa costante, quindi puoi utilizzare la monotonia dell'integrale come ha fatto il tuo professore e concludere che quell'integrale improprio converge (dal di sotto lo minori con lo $0$ perchè l'integranda è a segno costante positivo).
"Giuly19":
(dal di sotto lo minori con lo $0$ perchè l'integranda è a segno costante positivo).
(( vero. Grazie 
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo