Equazione con radici complesse

[luca7111]

Ciao a tutti! Sto cercando di risolvere un'equazione con radici complesse, in teoria è semplicissima ma c'è un errore che non riesco proprio a trovare, sicuramente stupido.
L'equazione è $z^4 + z^2 + 1 = 0$, ho posto $y = z^2$ e ho risolto l'equazione di secondo grado, ottenendo $y = -1/2 + sqrt(3)/2 i$ e $y = -1/2 - sqrt(3)/2 i$. Per trovare le soluzioni di z ho usato la formula di De Moivre, che mi dà i seguenti risultati:
$z_1 = e^(i pi/6) = sqrt(3)/2 + i/2$
$z_1 = e^(i pi 7/6) = -sqrt(3)/2 - i/2$
$z_1 = e^(-i pi/6) = sqrt(3)/2 - i/2$
$z_1 = e^(-i pi 7/6) = -sqrt(3)/2 + i/2$
Il problema è che secondo WolframAlpha queste soluzioni sono sbagliate, anzi sono le soluzioni dell'equazione $z^4 - z^2 + 1 = 0$. Cosa c'è che non va?
Grazie in anticipo!

[walter.ruggeri.3]

Risolviamo insieme l'equazione, passo per passo, in modo che tu possa trovare l'errore

Data $z^4+z^2+1=0$, effettuiamo (come tu hai suggerito) la sostituzione $y=z^2$, e otteniamo:

$y^2+y+1 = 0$

Risolviamo quest'equazione: si ha $ Delta = -3 < 0 $ (come ci potevamo aspettare, vista la richiesta del testo), e dunque tutte le soluzioni dell'equazione sono complesse, e precisamente sono:

$ y = (-1 +- sqrt(-3))/2 = (-1 +- isqrt(3))/2 = -1/2 +- sqrt(3)/2i $

Come sappiamo dalla nostra sostituzione, a ciascuna di queste soluzioni corrispondono due valori di $z$. Determiniamo questi valori: iniziamo con $ y = -1/2 + sqrt(3)/2i $ , e riscriviamolo in forma trigonometrica (che, ti ricordo, è del tipo $z = rho(costheta+isintheta)$ con $rho = sqrt(x^2 + y^2)$ e $costheta = x/rho ^^ sintheta = y/rho$): si ha $rho = sqrt((-1/2)^2 + (sqrt3/2)^2) = 1$ ed inoltre $ { ( costheta = -1/2 ),( sintheta = sqrt3/2 ):} $ , e cioè $theta = 2/3pi$; il nostro numero è pertanto
$y=cos(2/3pi)+isin(2/3pi)$
A questo punto, per calcolarne la radice quadrata, ci avvaliamo della (già da te citata) formula di De Moivre, dalla quale, ti ricordo, si ricava l'espressione $ sqrt(y) = sqrtrho(cos((theta + 2kpi)/2) + isin((theta + 2kpi)/2)) $, con $k = 0, 1$.
Applichiamo questa formula:

$k = 0 rArr sqrt(y) = sqrt1(cos(1/3pi) + isin(1/3pi)) = 1/2 + sqrt3/2i$

$k = 1 rArr sqrt(y) = sqrt1(cos(4/3pi) + isin(4/3pi)) = -1/2 - sqrt3/2i$


E così abbiamo già trovato due delle soluzioni; potremmo anche fermarci qui, perchè un noto teorema ci assicura che le altre due soluzioni sono le coniugate di queste due, ma per completezza ripetiamo il ragionamento già visto, applicandolo questa volta ad $ y = -1/2 - sqrt(3)/2i $. In questo caso, in forma goniometrica, otteniamo $ y = cos(4/3pi)+isin(4/3pi) $, e l'applicazione della formula sopra evidenziata ci permette di determinare le due soluzioni cercate:

$k = 0 rArr sqrt(y) = sqrt1(cos(2/3pi) + isin(2/3pi)) = -1/2 + sqrt3/2i$

$k = 1 rArr sqrt(y) = sqrt1(cos(5/3pi) + isin(5/3pi)) = 1/2 - sqrt3/2i$

E con questo, il nostro esercizio può dirsi concluso

Spero che una simile trattazione ti possa aiutare a chiarire i tuoi dubbi

[luca7111]

Ok, grazie mille, ma come ti sei ricavato quel $\theta = 4/3 pi$? Perché non prendere $\theta = pi/3$?

[RenzoDF]

"luca711":Ok, grazie mille, ma come ti sei ricavato quel $\theta = 4/3 pi$? Perché non prendere $\theta = pi/3$?

Quando cerchi l'argomento di un numero complesso con parte reale negativa dall' arcotangente del rapporto fra parte immaginaria e reale, devi ricordare di sommare (o sottrarre) 180° all'angolo ottenuto; l'arcotangente ti fornirà infatti un angolo nel primo quadrante con parte reale e immaginaria entrambe negative o positive e un angolo nel quarto quadrante per entrambi i casi di segni discordi, nel tuo caso quindi

$\theta=\pi/3+\pi=(4\pi)/3$

[walter.ruggeri.3]

"luca711":Ok, grazie mille, ma come ti sei ricavato quel $\theta = 4/3 pi$? Perché non prendere $\theta = pi/3$?

Guarda la circonferenza goniometrica:



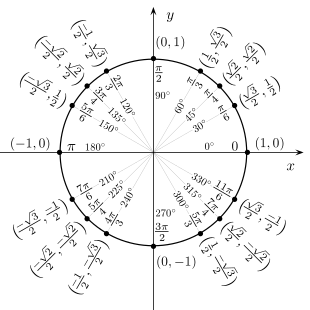
Noi sappiamo, dato che il nostro numero complesso è, in forma algebrica, $-1/2-sqrt3/2i$, che in forma goniometrica abbiamo $rho = sqrt((-1/2)^2+(-sqrt3/2)^2) = 1$, e dunque $ { ( costheta = x/rho = -1/2 ),( sintheta = y/rho = -sqrt3/2 ):} $. Ora, quale angolo della circonferenza goniometrica ha questo seno e questo coseno?