Dal grafico alla formula
Salve a tutti.
Avrei un problema presumo piuttosto banale per voi, e quindi se mi date una dritta ve ne sarei grato.
Il "dilemma" è questo: se ho un grafico di una funzione, come posso ricavare la formula matematica che soddisfi le caratteristiche?
In pratica il problema mi dice di tracciare una funzione da 0 a + infinito con codomimio anch'esso da zero a più infinito che sia strettamente decrescente e che il limite per x che tende a + infinito sia zero e che la la sua f ' (0) = 3.
Io il grafico l'ho disegnato tutto sul primo quadrante che parte da sopra e che scende con concavità verso l'alto fino a dove si annulla la sua derivata e poi la faccio scendere ancora concavità verso il basso scnde scende fino ad arrivare all'asse x senza però mai toccarlo.
Scusate se non allego il grafico ma ho difficoltà ad inserirlo e quindi capisco che può essere difficoltoso da parte vostra capire come ho tracciato la funzione.
Ma quello lo potrei rivedere.
Quello che invece non riesco a capire come devo procedere (guardando il grafico) per trovare la formula matematica che lo rappresenta.
Come si fa in generale?
Scusate se ho incasinato un pò le cose, ma conto sulla vostra intuizione.
Ringrazio anticipatamente per ogni vostra eventuale risposta.
Avrei un problema presumo piuttosto banale per voi, e quindi se mi date una dritta ve ne sarei grato.
Il "dilemma" è questo: se ho un grafico di una funzione, come posso ricavare la formula matematica che soddisfi le caratteristiche?
In pratica il problema mi dice di tracciare una funzione da 0 a + infinito con codomimio anch'esso da zero a più infinito che sia strettamente decrescente e che il limite per x che tende a + infinito sia zero e che la la sua f ' (0) = 3.
Io il grafico l'ho disegnato tutto sul primo quadrante che parte da sopra e che scende con concavità verso l'alto fino a dove si annulla la sua derivata e poi la faccio scendere ancora concavità verso il basso scnde scende fino ad arrivare all'asse x senza però mai toccarlo.
Scusate se non allego il grafico ma ho difficoltà ad inserirlo e quindi capisco che può essere difficoltoso da parte vostra capire come ho tracciato la funzione.
Ma quello lo potrei rivedere.
Quello che invece non riesco a capire come devo procedere (guardando il grafico) per trovare la formula matematica che lo rappresenta.
Come si fa in generale?
Scusate se ho incasinato un pò le cose, ma conto sulla vostra intuizione.
Ringrazio anticipatamente per ogni vostra eventuale risposta.
Risposte
In quale punto si annulla la derivata? La funzione è davvero strettamente decrescente?
in sintesi hai $f : [0,+infty) -> (0,+infty) text( tale per cui ) f'(x)<=0 text( da qualche parte), lim_(x->+infty) = 0, f'(0) = 3$
ti direi di scrivere un po' meglio i dati.... dove è negativa la derivata? in $(0,+infty)$? Sei sicuro che non sia $f(0) = 3$ anzichè $f'(0) = 3$?
quanto a trovare la funzione, non credo ce ne sia una sola... comunque in generale risalire dal grafico all'espressione analitica di una funzione è difficile e spesso non fattibile, tranne quando riesci a ricondurti a funzioni "standard" tipo $x^n, e^x, ln(x), sin(x)$ e via dicendo... controlla tutti i dati e scrivili decentemente, così magari riusciremo ad aiutarti
ti direi di scrivere un po' meglio i dati.... dove è negativa la derivata? in $(0,+infty)$? Sei sicuro che non sia $f(0) = 3$ anzichè $f'(0) = 3$?
quanto a trovare la funzione, non credo ce ne sia una sola... comunque in generale risalire dal grafico all'espressione analitica di una funzione è difficile e spesso non fattibile, tranne quando riesci a ricondurti a funzioni "standard" tipo $x^n, e^x, ln(x), sin(x)$ e via dicendo... controlla tutti i dati e scrivili decentemente, così magari riusciremo ad aiutarti
Ok... non ho l'esercizio davanti.
Stasera lo rivedrò meglio.
In ogni caso grazie vivamente per il tempo dedicatomi e scusate per come ho scritto sul forum.
La prossima volta cercherò di scrivere meglio.
Grazie ancora... vi disturbero
Stasera lo rivedrò meglio.
In ogni caso grazie vivamente per il tempo dedicatomi e scusate per come ho scritto sul forum.
La prossima volta cercherò di scrivere meglio.
Grazie ancora... vi disturbero
Scusami poll89 hai perfettamente ragione.
Ho rivisto l'esercizio:
f: $ [0,+oo ]rarr [0, +oo ] $ che sia continua e monotona strettamente decrescente, tale che f(0) = 3 e $ lim_(x -> +oo ) f(x) = 0 $
Ho rivisto l'esercizio:
f: $ [0,+oo ]rarr [0, +oo ] $ che sia continua e monotona strettamente decrescente, tale che f(0) = 3 e $ lim_(x -> +oo ) f(x) = 0 $
io ho tracciato un grafico del genere:
Direi che assomiglia molto a questo grafico, no? direi quindi che $3/(e^x)$ rispetta tutte le condizioni del problema, quindi puoi ben prenderla come funzione cercata.
Ora, io ci sono arrivato giusto perchè ho visto mille volte il grafico di $e^(-x)$ e quindi l'ho riconosciuto. Ci sono sicuramente altre funzioni che rispettano queste condizioni, però non conosco un algoritmo per determinarle esattamente. Per me bisogna solo andare ad esperienza in questi casi, e disegnare il grafico aiuta molto a riconoscere la presenza di funzioni "standard", come appunto $e^(-x)$.
direi quindi che $3/(e^x)$ rispetta tutte le condizioni del problema, quindi puoi ben prenderla come funzione cercata.Ora, io ci sono arrivato giusto perchè ho visto mille volte il grafico di $e^(-x)$ e quindi l'ho riconosciuto. Ci sono sicuramente altre funzioni che rispettano queste condizioni, però non conosco un algoritmo per determinarle esattamente. Per me bisogna solo andare ad esperienza in questi casi, e disegnare il grafico aiuta molto a riconoscere la presenza di funzioni "standard", come appunto $e^(-x)$.
grazie tante per l'aiuto.
Mi sei stato veramente utile.
Di nuovo grazie.
Mi sei stato veramente utile.
Di nuovo grazie.
Buongiorno, visto la grande disponibilità vorrei approfittare:
Non riesco a capire perchè non mi fa inserire le formule.
Comunque vediamo se mi riesco a far capire:
l'esercizio mi chiede di disegnare il grafico di una funzione con dominio (da - infinito a + infinito) e codominio in R che sia continua, monotono strettamente crescente e tale che f(0) = 2 , il limite per x che tende a - infinito sia = ad 1 ed il limite di x che tende a + infinito sia = a 3.
Io l'ho disegnata come riportato nel file allegato sopra (ma non so se sia corretto).
Comunque il mio problema principale resta sempre quello di scrivere la relativa formula matematica che descrive tale funzione.
Mi scuso per non aver editato le formule ma non capisco perchè non me li fa inserire e ringrazio anticipatamente per ogni eventuale vostra risposta.
Comunque vediamo se mi riesco a far capire:
l'esercizio mi chiede di disegnare il grafico di una funzione con dominio (da - infinito a + infinito) e codominio in R che sia continua, monotono strettamente crescente e tale che f(0) = 2 , il limite per x che tende a - infinito sia = ad 1 ed il limite di x che tende a + infinito sia = a 3.
Io l'ho disegnata come riportato nel file allegato sopra (ma non so se sia corretto).
Comunque il mio problema principale resta sempre quello di scrivere la relativa formula matematica che descrive tale funzione.
Mi scuso per non aver editato le formule ma non capisco perchè non me li fa inserire e ringrazio anticipatamente per ogni eventuale vostra risposta.
Una funzione il cui grafico somiglia a quello che hai postato è l'arcotangente:
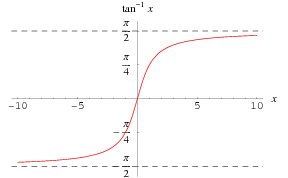
tuttavia ti rendi conto che ha come asintoti orizzontali $y=\frac{\pi}{2}$ e $y=-\frac{\pi}{2}$ e non passa per il punto $(0;2)$ ma per $(0;0)$. Vediamo come modificare la funzione arctan x in modo da soddisfare i requisiti richiesti.
Per prima cosa potremmo traslare il grafico verso l'alto aggiungendo 2 alla legge della funzione:
$$
y=2+\arctan x
$$
poi dobbiamo "restringerla" un po' in modo che abbia come asintoti le rette $y=3$ e $y=1$, questo è possibile farlo determinando $k$ in modo che la funzione $y=2+k\cdot \arctan x$ abbia tali rette come asintoti, cioè troviamo $k$ in modo che
$\lim_{x\rightarrow+\infty}(2+k\cdot \arctan x)=3$ e $\lim_{x\rightarrow-\infty}(2+k\cdot \arctan x)=1$ da cui
$\lim_{x\rightarrow+\infty}(2+k\cdot \arctan x)=2+k\frac{\pi}{2}$ allora $2+k\frac{\pi}{2}=3 iff k=\frac{2}{\pi}$
$\lim_{x\rightarrow-\infty}(2+k\cdot \arctan x)=2-k\frac{\pi}{2}$ allora $2-k\frac{\pi}{2}=1 iff k=\frac{2}{\pi}$.
Quindi il valore di $k$ cercato è $\frac{2}{\pi}$ allora la funzione da te cercata è $y=2+\frac{2}{\pi}arctan x$
tuttavia ti rendi conto che ha come asintoti orizzontali $y=\frac{\pi}{2}$ e $y=-\frac{\pi}{2}$ e non passa per il punto $(0;2)$ ma per $(0;0)$. Vediamo come modificare la funzione arctan x in modo da soddisfare i requisiti richiesti.
Per prima cosa potremmo traslare il grafico verso l'alto aggiungendo 2 alla legge della funzione:
$$
y=2+\arctan x
$$
poi dobbiamo "restringerla" un po' in modo che abbia come asintoti le rette $y=3$ e $y=1$, questo è possibile farlo determinando $k$ in modo che la funzione $y=2+k\cdot \arctan x$ abbia tali rette come asintoti, cioè troviamo $k$ in modo che
$\lim_{x\rightarrow+\infty}(2+k\cdot \arctan x)=3$ e $\lim_{x\rightarrow-\infty}(2+k\cdot \arctan x)=1$ da cui
$\lim_{x\rightarrow+\infty}(2+k\cdot \arctan x)=2+k\frac{\pi}{2}$ allora $2+k\frac{\pi}{2}=3 iff k=\frac{2}{\pi}$
$\lim_{x\rightarrow-\infty}(2+k\cdot \arctan x)=2-k\frac{\pi}{2}$ allora $2-k\frac{\pi}{2}=1 iff k=\frac{2}{\pi}$.
Quindi il valore di $k$ cercato è $\frac{2}{\pi}$ allora la funzione da te cercata è $y=2+\frac{2}{\pi}arctan x$
Ti ringrazio tantissimo.
mmm?
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo