Piccolo problema con gli insiemi

[Lando1]

ho un bel esercizietoo da fare
S è l'insieme di tutti i numeri naturali senza divisori quadrati
T è l'insieme dei numeri naturali con esattametnte tre fattori primi
U è l'insieme dei numeri naturali minori o uguali a 100

Domande:

A)
Cos'è l'intersezione dei 3 insiemi?

B)
è vero che (A intersecato B) unito C = (A unito C) intersecato (B unito C)?


Secondo me la risposta alla prima domanda è: insime vuoto!

Volendo scrivere simbolicamenter l'insieme S e l'insieme T come si può fare?

[Nidhogg]

[Lando1]

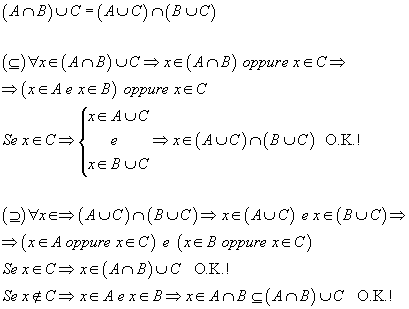
ciao! Grazie mille per la risposta: una domanda: cosa sono i due simboli che hai usati all'inizio della terza e della quinta riga?

[Nidhogg]

Sono i simboli dell'inclusione larga. Quando si dimostra un'uguaglianza fra insiemi, si dimostrano sempre le due inclusioni. La prima riguarda l'inclusione del primo insieme nel secondo, mentre la seconda il contrario. Ho usato quei simboli proprio per indicare dove inizia la dimostrazione della prima inclusione e dove inizia la dimostrazione della seconda. Spero di esserti stato di aiuto. Per altre delucidazioni chiedi pure.

[Lando1]

Ottimo leonardo! Ti ringrazio!
E per l'altre domande? la A e l'ultima relativa a come esprimere simbolicamente gli insiemi?

[Nidhogg]

Voglio essere sicuro di una cosa: ma dicendo "senza divisori quadrati", che intendi?

[Lando1]

È una bella domanda: me la sono posta anch'io e anche i mie compagni! eheh
Sul testo ci sta scritto proprio come te l'ho scritto io! Non ne so di più!

[Nidhogg]

Le risposte a questa domanda sostanzialmente sono due. La prima è che dicendo che un numero naturale non ha divisori quadrati, esso non ha divisori quadrati perfetti a meno che 1, e questo numero è denominato quadrato-libero. (Ad esempio 30=2*3*5, non ha divisori quadrati perfetti, mentre 60=2^2*3*5, ha un quadrato perfetto (4) come divisore). La seconda è: per ogni numero naturale n, l'insieme di tutti i divisori positivi di n forma un reticolo distributivo se scriviamo a <= b per a divide b. Questo reticolo è un'algebra booleana se e soltanto se per ogni n non vi sono divisori quadrati. Il più piccolo elemento,che in generale indichiamo con lo 0, in questa algebra booleana è il numero naturale 1; mentre l'elemento che usualmente indichiamo con l'1 in questi insiemi è l'elemento "n". Sinceramente penso sia più indicata la prima risposta visto l'esercizio. Comunque se puoi dirmi in che ambito state affrontando questi problemi, ti potrei essere di maggior aiuto.

[Lando1]

Noi per il momento abbiamo ripassato solamente un po' di logica matematica e gli insiemi e i concetti principali di funzione!

Una altro favore: ho provato a dimostrare una cosa, ma non sono riuscito ad arrivare fino in fondo! Come dimostreresti queso?

[Nidhogg]

[Principe2]

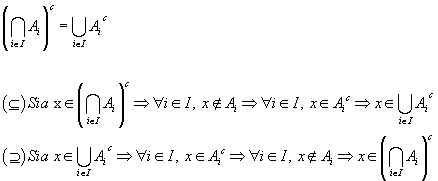
concordo con la definizione di Leonardo e con la denominazioen di "quadrato libero" o "libero da quadrati", dall'inglese "square-free"...

[Lando1]

Ragazzi i primi giorni di università sono veramente duri! Cmq i problemi persistono! Mi poteste aiutare a risolvere questo? (possibilmente spiegandomi un in maniera dettagliata la soluzione!) Grazie infinite, non so come farei senza di voi!