Trigonometria: dominio, codominio in disequazione

[Mr.Mazzarr]

Argomento trattato con un altro utente in un altro topic, ho pensato di aprirne uno singolare utile non solo a me.
Il topic è incentrato sulle funzioni trigonometrico, sul loro dominio e codominio e quindi come '' giostrarsi '' in casi di disequazione e campi d'esistenza.

Partiamo col scrivere le funzioni trigonometri con rispettivo dominio e codominio:

$y=sin x$: $R rarr [-1, 1]$
$y=cos x$: $R rarr [-1, 1]$
$y=tan x$: $R-{pi/2 + kpi} rarr R$

$y=arcsin x$: $[-1, 1] rarr [-pi/2, pi/2]$
$y=arccos x$: $[-1, 1] rarr [0, pi]$
$y=arctan x$: $(-oo, +oo) rarr (-pi/2, pi/2)$

Ora. Una omand:

- Come si osservano le funzioni trigonometriche in un caso di disequazione? Prendiamo, ad esempio, il campo d'esistenza di:

$log(arcsin(x+1))$

Essendo argomento del logaritmo, bisogna porre $arcsin(x+1) > 0$. Ed essendo argomento dell'arcoseno, bisogna porre $-1 < x < 1$. Sul secondo è molto semplice lavorare, ma sul primo che discorso devo fare?

[minomic]

Prendiamo $log[arcsin(x+1)]$. Devono valere ${(-1 <= x+1 <= 1), (arcsin(x+1) > 0):}$ (avevi dimenticato il $+1$).
Concentriamoci sulla seconda: l'arcoseno di $x+1$ è definito come quell'angolo (tra $-pi/2$ e $pi/2$) che ha come seno $x+1$. Chiedersi quando l'arcoseno è positivo significa quindi chiedersi quando questo angolo è positivo, ovvero compreso tra $0$ e $pi/2$. Questo significa che il suo seno sarà compreso tra $0$ e $1$, ma il suo seno, per la definizione che abbiamo appena dato, è proprio $x+1$ quindi il sistema diventa ${(-1 <= x+1 <= 1), (0 < x+1 <= 1):}$.

[burm87]

Sul secondo non bisogna porre $-1<=x+1<=1$?

Per quanto riguarda il primo invece credo sia sufficiente porre $0

Cita

Segnala

[Mr.Mazzarr]

"minomic":Prendiamo $log[arcsin(x+1)]$. Devono valere ${(-1 <= x+1 <= 1), (arcsin(x+1) > 0):}$ (avevi dimenticato il $+1$).
Concentriamoci sulla seconda: l'arcoseno di $x+1$ è definito come quell'angolo (tra $-pi/2$ e $pi/2$) che ha come seno $x+1$. Chiedersi quando l'arcoseno è positivo significa quindi chiedersi quando questo angolo è positivo, ovvero compreso tra $0$ e $pi/2$. Questo significa che il suo seno sarà compreso tra $0$ e $1$, ma il suo seno, per la definizione che abbiamo appena dato, è proprio $x+1$ quindi il sistema diventa ${(-1 <= x+1 <= 1), (0 < x+1 <= 1):}$.

L'arcoseno esiste tra $-1$ e $1$ e il suo codominio è $]-pi/2, pi/2[$. Così, possiamo dire che quando lavoro sull'argomento tengo conto del Dominio e quando lavoro su tutta la funzione tengo conto del Codominio?

[minomic]

"Mr.Mazzarr":possiamo dire che quando lavoro sull'argomento tengo conto del Dominio e quando lavoro su tutta la funzione tengo conto del Codominio?

Direi di sì.

[Mr.Mazzarr]

Molto bene

Una disequazione del tipo:

$arcsen(x+1) > 2$

Come si risolve?

[burm87]

Non ha soluzioni, avendo detto che l'arcoseno ha codominio $[−π/2,π/2]$ non potrà mai essere $>2$.

[minomic]

Esatto burm87.
Faccio un esempio risolvibile: $arcsin(x+1) > 1$.
Quel $1$ rappresenta un angolo in radianti, e tra $-pi/2$ e $pi/2$ il seno è crescente, quindi $x+1 > sin 1 rArr x > sin 1 - 1$.

[Mr.Mazzarr]

Mmm capito.

Ho incontrato una situazione un po' particolare..

$cos^2x > 1/2$

$cosx < -(sqrt(2))/2 uu cosx > (sqrt(2))/2$

Ora, ho analizzato singolarmente le disequazioni...

1. $cosx > -(sqrt(2))/2$

Dato che si lavora sugli archi per il passaggio a radianti, ho considerato quell'arco in cui il valore del coseno è inferiore a $-(sqrt(2))/2$. Ovvero l'arco che va da $3/4 pi$ a $5/4 pi$. Ed ho quindi scritto:

$3/4 pi + 2kpi < x < 5/4 pi + 2kpi$

2. $cosx < (sqrt(2))/2$

Anche qui ho fatto il discorso precedente, ho considerato l'arco del coseno nei punti inferiori a quel valore. Ovvero l'arco che va da $pi/4$ a $-pi/4$. Quindi ho scritto:

$1/4 pi + 2kpi < x < -1/4 pi + 2kpi$


Volevo sapere: E' esatto?

[minomic]

L'idea è giusta anche se poi hai fatto confusione tra maggiore e minore:
1. $cos x < -sqrt2/2 rArr 3/4 pi + 2k pi < x < 5/4 pi + 2k pi$
2. $cos x > sqrt2/2 rArr -pi/4 + 2k pi < x < pi/4 + 2k pi$

[Mr.Mazzarr]

Ma dato che la circonferenza trigonometrica va osservata in senso antiorario, il $pi/4$ in questo caso è l'inizio dell'arco da considerare mentre $-pi/4$ è la fine, no?

[minomic]

"Mr.Mazzarr":Ma dato che la circonferenza trigonometrica va osservata in senso antiorario, il $pi/4$ in questo caso è l'inizio dell'arco da considerare mentre $-pi/4$ è la fine, no?

Eh no, altrimenti prendi la parte sbagliata di circonferenza! Proprio perchè va osservata in senso antiorario sono partito da $-pi/4$ e sono arrivato a $pi/4$.
Ricorda che gli angoli con coseno maggiore di $sqrt2/2$ sono quelli che stanno "a destra" rispetto agli angoli con coseno uguale a $sqrt2/2$.

[Mr.Mazzarr]

Mmm il ragionamento di base l'ho anche capito, solo che se io vado da $-pi/4$ in su incontro $2pi$ e non $0$. No?

P.s.
Io all'esame non avrò le tabelle con me, perciò mino ti chiedo due cose:
- Qual è la formula per il calcolo dell'angolo in radianti ?
- Secondo te c'è un metodo per memorizzare al meglio la circonferenza trigonometrica ?

[Zero87]

"Mr.Mazzarr":- Qual è la formula per il calcolo dell'angolo in radianti ?

Se tu intendi da gradi a radianti, la formula più semplice, secondo me, è quella che ti ha suggerito gio73 non ricordo dove. Cioè, basta fare una semplice proporzione:
sai che $\pi$ (in radianti) equivale a $180^o$ (o che $2\pi$ è uguale a $360^0$, non importa)

allora metti su la proporzione:
$180^o$:$\pi$=$\text{angolo in gradi}$:$\text{angolo in radianti}$
poi uno dei due angoli lo conosci e per l'altro risolvi la proporzione.

PS.
Spero che non ti offenda questo post nell'english corner (sarebbe offensivo solo se odiassi il calcio... ma neanche il quel caso!)
viewtopic.php?f=25&t=109203&p=722354#p722354

[Mr.Mazzarr]

Si mi riferivo a quella formula.

Ti ho risposto in quel topic, non mi sono affatto offeso solo che non avevo letto il post!

[Zero87]

"Mr.Mazzarr":Ti ho risposto in quel topic, non mi sono affatto offeso solo che non avevo letto il post!

Ho pensato... Metti caso che odia il calcio e pensa che sia offensivo paragonare un calciatore ad un cestista... Intendevo che la mia era solo un'innocente somiglianza, per questo te l'ho detto!
(Un po' ci ho azzeccato dato che hai detto che Kobe plays the best sport in the world )

[Mr.Mazzarr]

In effetti odio il calcio, eccetto il Napoli per cui provo un amore viscerale. Ma qui siamo OT.

Tornando IT.
Quando mi trovo di fronte a disequazioni del tipo

$tg^2x > 1$

Mi conviene sempre portare nella forma $tgx = (senx)/cosx$ ??

[minomic]

No, ti conviene dire che $tan^2 x > 1$ equivale a $tan x < -1 vv tan x > 1$ e risolvere da qui.

[Zero87]

"Mr.Mazzarr":In effetti odio il calcio, eccetto il Napoli per cui provo un amore viscerale. Ma qui siamo OT.

[size=85]Il tuo nick, infatti, mi suonava familiare (in ambito del Napoli)...[/size]

Comunque

"Mr.Mazzarr":Tornando IT.
Quando mi trovo di fronte a disequazioni del tipo

$tg^2x > 1$

Mi conviene sempre portare nella forma $tgx = (senx)/cosx$ ??

Io, personalmente, penso che il modo migliore sia
$tg^2 (x)-1>0$
e fare uno studio del segno "vecchio stile". In questo caso, se vuoi farlo "sbrigativo", puoi porre $tg(x)=t$ e studiare $t^2-1>0$ per poi riportarti alla tangente una volta trovato l'intervallo.

Comunque, in generale, il metodo dipende dai casi. Personalmente, però, se va la fattorizzazione, mi rimane semplice lo studio del segno (ma questa è un'opinione personale).

EDIT.
minomic ha risposto in contemporanea e ha detto quello che ho detto anche io (anche se lui ha esposto direttamente la soluzione sottointendendo il $tg^2(x)-1>0$).

buon fine settimana, forumisti

[Mr.Mazzarr]

In quel caso la $t$ va posta agli estremi:

$t < -1$ $uu$ $t > 1$

Pongo la tangente e la studio.
Ma come si studia la tangente sulla circonferenza trigonometrica? Oppure non la posso studiare da lì e devo solo cavarmela un po' a mente con i valori in radianti?

[minomic]

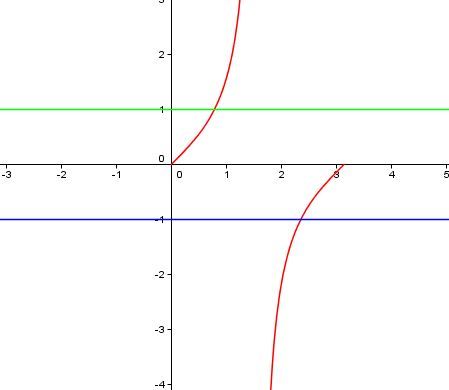
Esiste un metodo per studiare la tangente direttamente sulla circonferenza ma personalmente non me lo ricordo mai e lo ritengo poco comodo. Invece suggerisco di prendere direttamente il grafico della tangente tra $0$ e $pi$ ed analizzare le zone che ci interessano.

Noi vogliamo i valori esterni a $+- 1$ quindi le parti sotto la retta blu o sopra la verde. I punti di intersezione tra il grafico della tangente e le due rette sono $x= +- pi/4$, quindi la nostra soluzione sarà $x in (pi/4, pi/2) uu (pi/2, 3/4pi)$ più ovviamente la periodicità della tangente, cioè $k pi$.