Ricavare x

[jhs1]

Buongiorno, purtroppo le mie conoscenze di matematica derivate dall'ITIS di qualche ventennio fà sono un po' arrugginite.
Ho trovato in un libro che sto leggendo questa equazione (la riporto esattamente come è scritta sul libro e in forma più leggibile):
S=KA(B-C)((1-3XC/A)^(1-2/X)-1)/D^2/(2-X)

$S=KA(B-C)((1-3XC/A)^(1-2/X)-1)/D^2/(2-X)$
dati S,K,A,B,C,D vorrei ricavare X.
Il mio problema è che avendo l'incognita sia nella base,nell'esponente, e nell'ultima parentesi, non riesco a ricavarla.
Potreste darmi un aiuto?

[moccidentale]

.

[jhs1]

Certo, l'unico esempio che ho con me ora è questo che riporta i seguenti valori per l'equazione:
A=4370 B=1500 C=954 D=3000 K= 1158 e X=0.5 da cui risulta S=303.5. Per quanto riguarda i valori di X, vale sempre il vincolo: X>0
Eventualmente più tardi quando rientro controllo nel libro.

[moccidentale]

.

[jhs1]

Non sono molto pratico a scrivere le formule al PC, non riesco a scriverla bene;
$S=KA(B-C){(1-\frac(3XC)(A))^(1-2/X)-1}$
il tutto diviso per $D^2$ e poi diviso ancora per $(2-X)$
Sostituendo con i dati sopra S dovrebbe risultare corretto approssimando i decimali.

[moccidentale]

.

[jhs1]

Hai perfettamente ragione, ho sbagliato io a copiare il risultato negli appunti!! Il risultato che riporta il libro è 468.2, in linea con quanto hai calcolato tu.

[pistacios]

Scusate se mi infilo in mezzo

Ad esempio, ciò accade anche in un'equazioncina del tipo: \[
e^x-x-2=0
\]

Per curiosità, come posso capire quando in effetti non è esplicitabile in funzioni elementari (in modo inequivocabile)? Aka come ti è venuto quell'esempietto? Perché se ci penso mi rimane una tavola bianca e non mi vengono idee (o se mi vengono non ho la certezza che non sia in effetti esplicitabile ma non sia io capace)

[Faussone]

"pistacios":Per curiosità, come posso capire quando in effetti non è esplicitabile in funzioni elementari (in modo inequivocabile)? Aka come ti è venuto quell'esempietto? Perché se ci penso mi rimane una tavola bianca e non mi vengono idee (o se mi vengono non ho la certezza che non sia in effetti esplicitabile ma non sia io capace)

Non è che ci sia una regola, provi a ricavare $x$ e te ne rendi conto, un buon indizio è quando appaiono funzioni non algebriche trascendenti (come esponenziali, logaritmi ecc).

Comunque se si vuole ricavare la $x$ quando quella $S=0$ allora credo non ci siano soluzioni nei numeri reali[nota]Nei reali la funzione esiste solo per $x

Cita

Segnala

[jhs1]

"Faussone":[quote="pistacios"]Per curiosità, come posso capire quando in effetti non è esplicitabile in funzioni elementari (in modo inequivocabile)? Aka come ti è venuto quell'esempietto? Perché se ci penso mi rimane una tavola bianca e non mi vengono idee (o se mi vengono non ho la certezza che non sia in effetti esplicitabile ma non sia io capace)

Non è che ci sia una regola, provi a ricavare $x$ e te ne rendi conto, un buon indizio è quando appaiono funzioni non algebriche trascendenti (come esponenziali, logaritmi ecc).

Comunque se si vuole ricavare la $x$ quando quella $S=0$ allora credo non ci siano soluzioni nei numeri reali[nota]Nei reali la funzione esiste solo per $x No, X non può mai essere 0 e nemmeno S. A me interessa ricavare X dati gli altri coefficienti, che sono sempre maggiori di 0.
Nell'esempio S=468.146 (il testo approssima a 468.2).

[moccidentale]

.

[Faussone]

"jhs":
No, X non può mai essere 0 e nemmeno S. A me interessa ricavare X dati gli altri coefficienti, che sono sempre maggiori di 0.
Nell'esempio S=468.146 (il testo approssima a 468.2).

Ah ok, avevo frainteso.

[pistacios]

un buon indizio è quando appaiono funzioni non algebriche trascendenti (come esponenziali, logaritmi ecc).

Sisi, questo è verissimo ma non è sufficiente (diciamo che è vero tendenzialmente). Quindi mi aveva incuriosito come torvare un controesempio furbo come ha fatto sellacolle.

[axpgn]

"sellacollesella":e applicando il metodo più semplice in assoluto, ossia il metodo di bisezione, abbiamo:

[*:hgzgry9u] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.001,0.764]\) e \(c = 0.3823\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.3823,0.764]\) e \(c = 0.5729\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.3823,0.5729]\) e \(c = 0.4776\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.4776,0.5729]\) e \(c = 0.5252\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.4776,0.5252]\) e \(c = 0.5014\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.4776,0.5014]\) e \(c = 0.4895\);

[/*:m:hgzgry9u]
[*:hgzgry9u] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.4895,0.5014]\) e \(c = 0.4954\);[/*:m:hgzgry9u][/list:u:hgzgry9u]
e così via finché ci si ritiene soddisfatti dall'approssimazione: \(X \approx 0.500\).

oppure se non sei sellacollesella puoi usare Wolfram Alpha

[jhs1]

"sellacollesella":[quote="jhs"]Il risultato che riporta il libro è 468.2, in linea con quanto hai calcolato tu.

Ottimo! Assodato ciò, tornando all'equazione che avevi scritto in modo corretto sin dal principio: \[
\underbrace{S - \frac{KA(B-C)}{D^2(2-X)}\left[\left(1-\frac{3C}{A}X\right)^{1-\frac{2}{X}}-1\right]}_{f(X)} = 0
\] affinché abbia senso nel campo dei numeri reali dobbiamo imporre: \[
1 - \frac{3C}{A}X > 0
\] e tenendo conto che tutti i parametri sono positivi, tra cui \(X>0\), porta a scrivere: \[
0 < X < \frac{A}{3C} = 1.5269.
\] Pertanto, tenuto conto che:

[*:35fek1lo] \(f\) è continua in \((0,1.5269)\);

[/*:m:35fek1lo]
[*:35fek1lo] \(\begin{aligned}\lim_{X \to 0^+}\end{aligned} f(X) > 0\);

[/*:m:35fek1lo]
[*:35fek1lo] \(\begin{aligned}\lim_{X \to 1.5269^-}\end{aligned} f(X) < 0\);[/*:m:35fek1lo][/list:u:35fek1lo]
il teorema degli zeri assicura che \(f\) abbia almeno uno zero in tale intervallo e considerando anche il fatto
che \(f\) è monotona decrescente allora lo zero è unico e può essere approssimato con un metodo a piacere.

In particolare, dato che agli estremi \(f\) può essere valutata solo al limite, ci riduciamo all'intervallo: \[
[a,b] := [0.001, 1.526]
\quad \quad \Rightarrow \quad \quad
c := \frac{a+b}{2} = 0.764
\] e applicando il metodo più semplice in assoluto, ossia il metodo di bisezione, abbiamo:



[*:35fek1lo] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.001,0.764]\) e \(c = 0.3823\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.3823,0.764]\) e \(c = 0.5729\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.3823,0.5729]\) e \(c = 0.4776\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.4776,0.5729]\) e \(c = 0.5252\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.4776,0.5252]\) e \(c = 0.5014\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)<0\) allora \([a,b]=[0.4776,0.5014]\) e \(c = 0.4895\);

[/*:m:35fek1lo]
[*:35fek1lo] dato che \(f(a)f(c)>0\) allora \([a,b]=[0.4895,0.5014]\) e \(c = 0.4954\);[/*:m:35fek1lo][/list:u:35fek1lo]
e così via finché ci si ritiene soddisfatti dall'approssimazione: \(X \approx 0.500\).



"pistacios":Per curiosità, come posso capire quando in effetti non è esplicitabile in funzioni elementari?


Non conosco alcuna regola generale, tant'è che anche l'equazioncina che ho proposto come esempio ha soluzione reale esprimibile in forma chiusa, ma coinvolgendo la funzione W di Lambert non ne ho tenuto conto, non essendo nella cerchia delle cosiddette funzioni elementari a cui solitamente si fa riferimento.

In linea di principio, l'obiettivo è quello di ricondursi ad un sistema di equazioni polinomiali per le quali, perlomeno numericamente, risulta sempre possibile determinarne tutte le soluzioni in campo complesso; in caso contrario le cose si fanno mooolto più complicate e occorre capire di volta in volta come uscirne vivi. [/quote]
devo studiarmi il tutto, per ora è un po' oltre le mie conoscenze..
Essendo che vorrei scrivere del codice per risolverla, ed ho dato un occhio a come altri hanno risolto il problema, capisco perchè non hanno tentato di risolvere l'equazione, ma per ci sono arrivati per iterazioni partendo da un valore noto aumentando o diminuendo X fino ad arrivare ad un valore vicino e accettabile..

Ricontrollando il testo mi sono accorto di un paio di dettagli che non avevo riportato negli appunti:
X può essere anche <0 (negativo) ma non 0. Mentre gli altri valori sono tutti sempre positivi e maggiori di 0.

[moccidentale]

.

[axpgn]

"sellacollesella":Ma, volendo, si può fare a meno di scrivere righe di codice e usare un foglio Excel;

... che funziona benissimo per cose del genere, cinque minuti e hai finito ...

[moccidentale]

.

[axpgn]

Ma tu sei troppo raffinato , hai ricostruito in Excel quello che avresti fatto con un programma; io sarei stato molto ma molto più brutale: una volta individuato l'intervallo, si immette la formula, la si ricopia cento volte, si inserisce l'incognita da un estremo all'altro dell'intervallo con passi di un centesimo e casomai si raffina rimpicciolendo l'intervallo e il passo; l'unica finezza la legenda con le variabili come hai fatto tu.

Cordialmente, Alex

[moccidentale]

.

[utente__medio11]

"axpgn":Ma tu sei troppo raffinato , hai ricostruito in Excel quello che avresti fatto con un programma; io sarei stato molto ma molto più brutale: una volta individuato l'intervallo, si immette la formula, la si ricopia cento volte, si inserisce l'incognita da un estremo all'altro dell'intervallo con passi di un centesimo e casomai si raffina rimpicciolendo l'intervallo e il passo;

Io avrei fatto ancora prima:







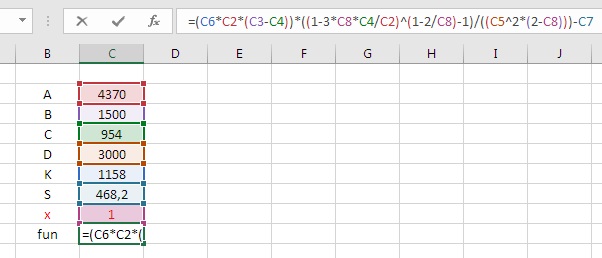
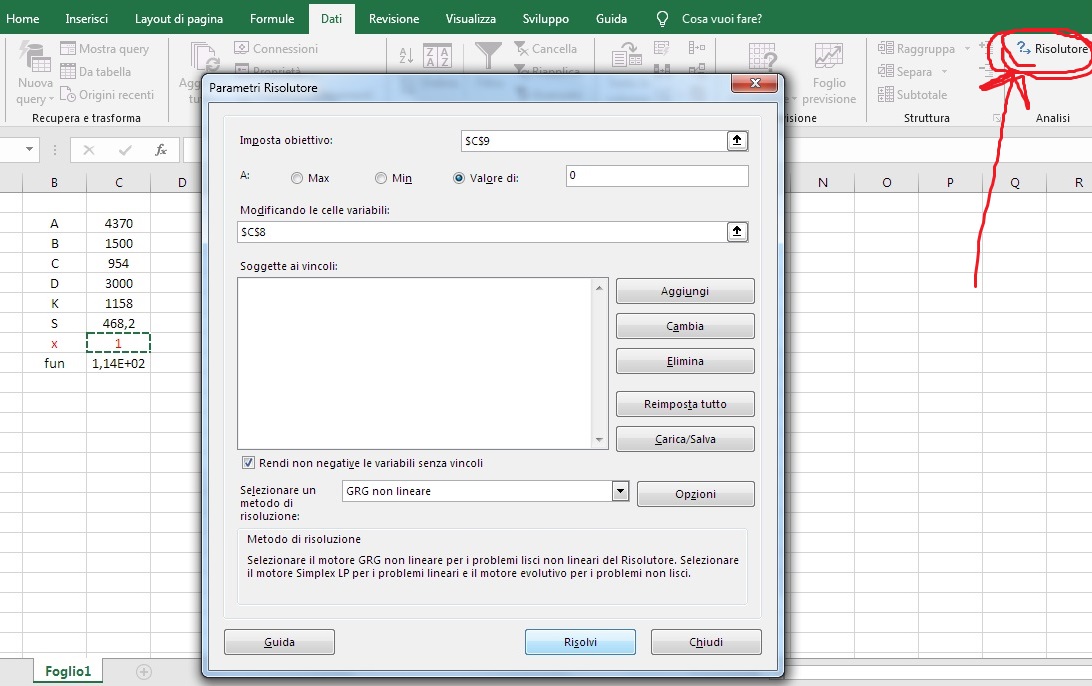
Una volta che si vuole usare excel, tanto vale farlo fino in fondo!