Radice quadrata
Scusate, ma nn riesco proprio a capire come si arriva a questa soluzione
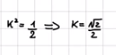
che venga uguale mi sta bene, ma perchè scriverlo in questa forma e come? grazie
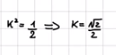
che venga uguale mi sta bene, ma perchè scriverlo in questa forma e come? grazie
Risposte
$K^2=1/2$
$K=sqrt(1/2)$
$K=1/sqrt2$
$K=1/sqrt2*sqrt2/sqrt2$
$K=sqrt2/2$
$K=sqrt(1/2)$
$K=1/sqrt2$
$K=1/sqrt2*sqrt2/sqrt2$
$K=sqrt2/2$
thanks
Innanzitutto credo che il problema sia più adatto alla sezione secondaria di secondo grado; dubito che alle medie si facciano le equazioni di secondo grado.
In ogni caso rispondo al "perché scriverlo in quella forma":
$K^2=1/2$ é un' equazione e come tale devi risolverla. É come scrivere $2x=1$; devi trovare il valore della x.
Per quanto riguarda la razionalizzazione devi fidarti del fatto che lasciare un numero irrazionale a denominatore é un po' un casino (ce ne accorgeremo più avanti), per questo é meglio toglierlo moltiplicando per uno. I tipi di razionalizzazione sono quattro.
Credo inoltre che tu abbia commesso un errore: prima dell'$1/2$ avresti dovuto mettere il $+-$.
Se hai dei dubbi non esitare a farti sentire!
In ogni caso rispondo al "perché scriverlo in quella forma":
$K^2=1/2$ é un' equazione e come tale devi risolverla. É come scrivere $2x=1$; devi trovare il valore della x.
Per quanto riguarda la razionalizzazione devi fidarti del fatto che lasciare un numero irrazionale a denominatore é un po' un casino (ce ne accorgeremo più avanti), per questo é meglio toglierlo moltiplicando per uno. I tipi di razionalizzazione sono quattro.
Credo inoltre che tu abbia commesso un errore: prima dell'$1/2$ avresti dovuto mettere il $+-$.
Se hai dei dubbi non esitare a farti sentire!
Uno dei problemi che mi ha accompagnato durante il liceo è il considerare le equazioni troppo meccanicamente. Me ne sono accorto troppo tardi e, anche se utenti sicuramente più esperti di me ti hanno fornito una risposta, voglio cercare di farti ragionare in un modo che senza dubbio ti sarà utile. Considera l'equazione come un'uguaglianza: tutto quello che è a sinistra dell'uguale deve essere uguale a tutto quello che è a destra dell'uguale affinché questa uguaglianza sia soddisfatta. Perciò con cos'altro puoi soddisfare l'uguaglianza \(\displaystyle k^2=1/2 \) ? Se al posto di scrivere \(\displaystyle k^2 \) vuoi scrivere \(\displaystyle k \) a sinistra dell'uguaglianza per fare sì che l'uguaglianza sia ancora la stessa a sinistra si dovrà trovare qualcosa che elevato al quadrato sarà uguale a \(\displaystyle k^2 \) . Guarda caso, se elevi al quadrato la radice quadrata di \(\displaystyle 1/2 \) , ottieni proprio \(\displaystyle 1/2 \). Quindi \(\displaystyle k= \) \(\displaystyle \sqrt[2]{1/2} \) Per quanto riguarda il resto hanno ragione gli altri utenti.
Il ragionamento é buono, però dimentichi anche tu il $-sqrt(1/2)$.
Per molto tempo mi chiedevo come si facesse lo stesso ragionamento con $2/π * ∫ sinπ/4(2^5 + 2)/sqrt(2(1 - x^2)) dx = 17$, ad esempio (l'ho inventato, tanto per scrivere qualcosa di complicato); ma la logica mi ha fatto capire col tempo che una volta intuito il concetto primitivo, lo si può estendere nella maniera più ampia possibile, senza doverne necessariamente comprendere l'integritá.
Per molto tempo mi chiedevo come si facesse lo stesso ragionamento con $2/π * ∫ sinπ/4(2^5 + 2)/sqrt(2(1 - x^2)) dx = 17$, ad esempio (l'ho inventato, tanto per scrivere qualcosa di complicato); ma la logica mi ha fatto capire col tempo che una volta intuito il concetto primitivo, lo si può estendere nella maniera più ampia possibile, senza doverne necessariamente comprendere l'integritá.
Sì, hai ragione. Quel messaggio in effetti era più che altro un modo per prendere familiarità con il MathJax. Quella che ho fornito io comunque è una delle soluzioni, era tanto per fare un esempio, a questo livello didattico si può ragionare in questo modo con tranquillità. Magari più avanti cessa di essere utile. Il problema è che io, personalmente, sono arrivato ai test di ingresso universitari senza aver questo concetto chiaro in mente, ma magari facevo più attenzione a non fare l'errore che ho fatto adesso, con grosso sforzo di tipo mnemonico.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo