Problemi che hanno come modello la parabola

[Miranda1313]

Ciao a tutti, potete darmi una mano con questa problema :"Un ponte su un fiume è formato da una sola arcata parabolica. Il ponte è lungo 80 m ed il punto centrale dell'arcata parabolica è posto ad un'altezza di 20 m rispetto all'acqua. Stabilisci quale può essere l'altezza di un'imbarcazione che naviga a 30 m dal centro del fiume, perché riesca a passare sotto il ponte".
Risultato: Inferiore a 8,75 m.
Grazie mille in anticipo.

[Lo_zio_Tom]

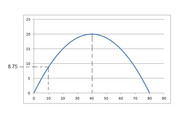
Il ponte in questione puoi vederlo come una parabola con i rami rivolti verso il basso che interseca l'origine del tuo sistema cartesiano e quindi una parabola di equazione

[math]y=a x^{2}+bx[/math]

Fai un disegno e te ne rendi conto subito....disegni una parabola con i rami rivolti verso il basso e che interseca l'origine degli assi. In base alle informazioni dell'esercizio, il vertice avrà coordinate

[math](40;20)[/math]

e la barca dovrà passare sotto al ponte ad una distanza di 10 metri da una delle due intersezione con le ascisse (ovvero a 30 metri dall'ascissa del vertice).



(cliccami per ingrandirmi)



Ricordando le coordinate del vertice e ricordando inoltre che nel nostro caso

[math]c=0[/math]

, basta metterle a sistema ottenendo

[math]\begin{cases}-\frac{b}{2a}=40\\-\frac{b^{2}}{4a}=20\end{cases}[/math]

Risolvi il sistema in

[math](a;b)[/math]

e trovi subito l'equazione richiesta:

[math]y=-\frac{x^{2}}{80}+x[/math]

A questo punto hai finito: altezza massima della barca è il punto di ordinata corrispondente all'ascissa

[math]x=10[/math]

oppure all'ascissa

[math]x=70[/math]

, come preferisci

In entrambi i casi, sostituendo nell'equazione della parabola, trovi

[math]y=8.75[/math]

[Miranda1313]

Grazie di cuore!