Problema Geometria Analitica Semplicissimo
Abbiamo un triangolo rettangolo ISOSCELE ABC che ha x estremi A(-1, 2) e B(3, -4). Determinare il terzo vertice C
le 2 condizioni sono
AB^2 = AC^2 + BC^2
AC = BC
Mi esce solo 1 risultato C(-2, -3)
..l'altro no...
le 2 condizioni sono
AB^2 = AC^2 + BC^2
AC = BC
Mi esce solo 1 risultato C(-2, -3)
..l'altro no...
Risposte
l'altro punto ha coordinate (4,1) basta che intersechi la retta per A parallela a BC con quella per B parallela ad AC
Se il punto C che hai trovato è giusto allora l'altro puoi calcolarlo così
ciao:yes
Se il punto C che hai trovato è giusto allora l'altro puoi calcolarlo così
ciao:yes
e lo so ke C(4,1)..dopo ke m'è uscita l'equazione di 2° grado con l'incognita y m sn usciti 2 valori: -3 e -5/13..quando sostituivo alla x -5|13 nn usciva..
Utilizzando la seconda condizione ottieni che la prima diventa: AB^2= 2AC^2
se chiami con x,y le coordinate di C ti viene fuori l'equazione di un cerchio di raggio AB^2 mezzi e centro in A.
Questo vuol dire che i punti C si trovano sul cerchio, ma dobbiamo individuarli (parlo al plurale perché son due i punti).
Sarebbe conveniente disegnare un cerchio con sopra i punti A e B.
Adesso se si guarda il disegno si capisce che il punto C lo trovo intersecando l'asse del segmento AB con la circonferenza.
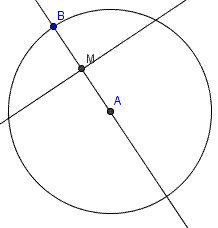
L'asse del segmento è la retta che passa per il suo punto medio. La scelgo perché sò che il triangolo deve essere isoscele. Quindi l'altezza tracciata dal vertice C cade sul punto medio del segmento AB.
L'intersezione della retta con il cerchio da come risultato i due punti cercati.
se il prof ha usato altri criteri scrivili sotto. Quello che ho messo io mi sembra il più semplice.
ciao:beer
se chiami con x,y le coordinate di C ti viene fuori l'equazione di un cerchio di raggio AB^2 mezzi e centro in A.
26=(x+1)^2+(y-2)^2
Questo vuol dire che i punti C si trovano sul cerchio, ma dobbiamo individuarli (parlo al plurale perché son due i punti).
Sarebbe conveniente disegnare un cerchio con sopra i punti A e B.
Adesso se si guarda il disegno si capisce che il punto C lo trovo intersecando l'asse del segmento AB con la circonferenza.
L'asse del segmento è la retta che passa per il suo punto medio. La scelgo perché sò che il triangolo deve essere isoscele. Quindi l'altezza tracciata dal vertice C cade sul punto medio del segmento AB.
L'intersezione della retta con il cerchio da come risultato i due punti cercati.
se il prof ha usato altri criteri scrivili sotto. Quello che ho messo io mi sembra il più semplice.
ciao:beer
no ancora non l'abbiamo corretto ma abbiamo sempre usato metodi semplici senza dilungarsi in futilità...
cmq cerco d rifarlo con calma, sai ormai è sfida xsonale..
cmq grazie 1000 x l'attenzione e x la pazienza :) :)
cmq cerco d rifarlo con calma, sai ormai è sfida xsonale..
cmq grazie 1000 x l'attenzione e x la pazienza :) :)
Questa discussione è stata chiusa
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo