Esercizio mediana

[mombe1]

Buongiorno a tutti. Vi riporto un esercizio di statistica descrittiva che non mi risulta molto chiaro. Questo il testo:

In una seriazione a classi di intervallo la mediana occupa il 32° posto e si trova all'interno della classe 10-25 avente come frequenza cumulata 41. Sapendo che la frequenza cumulata della classe precedente è 29, la mediana ha valore 13,75. Perché?

Dal fatto che la mediana occupi il 32° posto, ho dedotto che la popolazione è composta da 63 elementi. La frequenza della classe 10-25 risulta essere di 41-29 = 12.
Da qui non riesco a proseguire...

Grazie a chi vorrà aiutarmi!

[Lo_zio_Tom]

Con $F$ indico la distribuzione cumulata delle frequenze

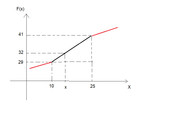
$(F(25)-F(10))/(25-10)=(32-F(10))/(x-10)$

$(41-29)/(25-10)=(32-29)/(x-10)$

risolvi in $x$ e trovi appunto $x=13.75$


spiegazione:

Dato che la distribuzione è per classi, ciò significa che la distribuzione cumulata è una spezzata. Ho indicato con il segmento in nero la parte di spezzata nota dai dati ed in rosso una eventuale possibile distribuzione del fenomeno (non ci interessa per il problema).
Sappiamo che la mediana coincide con il cumulato 32 e quindi non resta che calcolare l'ascissa $x$ in figura. (senza ricopiare la formula della retta che passa per due punti assegnati osservo che in triangoli simili il rapporto fra i cateti è costante....)

(click sull'immagine per ingrandire)

"mombe":
Dal fatto che la mediana occupi il 32° posto, ho dedotto che la popolazione è composta da 63 elementi.

In generale questo è falso!