Dubbio disequazione logaritmica
Ciao,
non riesco a risolvere la seguente disequazione.
\(\displaystyle 2ln (x) - 3 < (2ln (x) + 3)/ln(x) \)
La soluzione sarebbe:
\(\displaystyle 0 < 1/ \sqrt(e) V 1 < x < e^3 \)
Di seguito i miei passaggi.
Riscrivo la disequazione in questa forma:
\(\displaystyle ln (x)^2 - ln(e)^3 < (2ln (x) + 3ln(e))/ln(x) \)
\(\displaystyle ln (x)^2 - ln(e)^3 < (ln (x)^2 + ln(e)^3)/ln(x) \)
moltiplicando entrambi i membri per \(\displaystyle ln (x) \)
avremo:
\(\displaystyle ln (x)^3 - ln(x) ln(e)^3 < ln (x)^2 + ln(e)^3 \)
\(\displaystyle ln (x)^3 - ln(x) ln(e)^3 - ln (x)^2 - ln(e)^3 < 0 \)
ovvero
\(\displaystyle ln (x)^3 - 3 ln(x) - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle ln (x)^3 - ln(x)^3 - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle - ln (x)^2 < ln(e)^3 \)
\(\displaystyle ln (x)^2 > ln(e)^3 \)
\(\displaystyle ln (x)^2 - ln(e)^3 > 0 \)
\(\displaystyle ln (x)^2 > ln(e)^3 \)
la base del logaritmo è > 0
si mette a sistema:
1. \(\displaystyle (x) > 0 \)
2. \(\displaystyle ln (x)^2 > ln(e)^3 \)
sto procedendo bene?
non riesco a risolvere la seguente disequazione.
\(\displaystyle 2ln (x) - 3 < (2ln (x) + 3)/ln(x) \)
La soluzione sarebbe:
\(\displaystyle 0 < 1/ \sqrt(e) V 1 < x < e^3 \)
Di seguito i miei passaggi.
Riscrivo la disequazione in questa forma:
\(\displaystyle ln (x)^2 - ln(e)^3 < (2ln (x) + 3ln(e))/ln(x) \)
\(\displaystyle ln (x)^2 - ln(e)^3 < (ln (x)^2 + ln(e)^3)/ln(x) \)
moltiplicando entrambi i membri per \(\displaystyle ln (x) \)
avremo:
\(\displaystyle ln (x)^3 - ln(x) ln(e)^3 < ln (x)^2 + ln(e)^3 \)
\(\displaystyle ln (x)^3 - ln(x) ln(e)^3 - ln (x)^2 - ln(e)^3 < 0 \)
ovvero
\(\displaystyle ln (x)^3 - 3 ln(x) - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle ln (x)^3 - ln(x)^3 - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle - ln (x)^2 - ln(e)^3 < 0 \)
\(\displaystyle - ln (x)^2 < ln(e)^3 \)
\(\displaystyle ln (x)^2 > ln(e)^3 \)
\(\displaystyle ln (x)^2 - ln(e)^3 > 0 \)
\(\displaystyle ln (x)^2 > ln(e)^3 \)
la base del logaritmo è > 0
si mette a sistema:
1. \(\displaystyle (x) > 0 \)
2. \(\displaystyle ln (x)^2 > ln(e)^3 \)
sto procedendo bene?
Risposte
Banalmente, poni t=lnx. Otterrai una disequazione razionale fratta, che risolta ti fornirà: t<-1/2 v 0
Azz hai ragione, c'ho perso 2 settimane a capirlo 
"giamar":
moltiplicando entrambi i membri per \(\displaystyle ln (x) \)
Attenzione, in una disequazione non puoi moltiplicare ambo i membri a cuor leggero perché se moltiplichi ambo i membri per una quantità negativa devi cambiare il verso della disequazione.
Nelle disequazioni in genere si raccoglie, si fa il mcm e si porta tutto in uno dei due membri per fare lo studio del segno.
Mi sembrava doveroso fare questa specifica - a prescindere dal metodo risolutivo impiegato.
Grazie ragazzi!
Un dubbio:
la disequazione di secondo grado ha come risultato
\(\displaystyle -1/2 < t < 3 \)
quindi \(\displaystyle X < e^3 \) e \(\displaystyle X > 1/ \sqrt (e) \)
non mi torna \(\displaystyle X < 1/ \sqrt (e) \)
la disequazione di secondo grado ha come risultato
\(\displaystyle -1/2 < t < 3 \)
quindi \(\displaystyle X < e^3 \) e \(\displaystyle X > 1/ \sqrt (e) \)
non mi torna \(\displaystyle X < 1/ \sqrt (e) \)
@giamar, mi dispiace dirlo ma non hai la più pallida idea di come approcciare questi problemi.
La disequazione è di una banalità imbarazzante (per uno che ha come obiettivo un esame di Analisi all'Università). Quindi, il consiglio che ti posso dare è abbandonare gli esercizi e metterti a studiare profondamente la teoria.....poi ovviamente fai ciò che ti pare e che ritieni più opportuno.
Testo[nota]anche se si tratta di logaritmi naturali viene più comodo usare sempre la notazione $log$...tanto si usano sempre quelli...[/nota]:
$2logx-3<(2logx+3)/(logx)$
La PRIMA COSA DA FARE....e che non hai fatto, se non solo parzialmente ed alla fine... è indicare le condizioni di esistenza....ovvero
${{: ( x>0 ),( x !=1 ) :}$
fatto questo (mettiamo la condizione nel cassetto e la tireremo fuori alla fine....)
non servono tutti quei passaggi che continui a fare ogni volta (senza peraltro ragionare sul problema) ma si porta tutto al membro di sinistra così, facendo come sempre il mcm e sommando i vari addendi:
$(2log^2 x-5logx-3)/(logx)<0$
(nota che non ho eliminato il denominatore perché è una disequazione....)
ora studiamo separatamente il segno del numeratore e del denominatore[nota]indico con la riga continua l'intervallo dove il numeratore (N) oppure il denominatore (D) risultano maggiori di zero mentre con quella tratteggiata dove essi risultano minori di zero[/nota]:
(click per ingrandire)
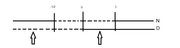
ora vedi bene che, affinché il rapporto sia minore di zero, i due intervalli in cui la disequazione è verificata sono quelli dove ci ho messo la freccia (come peraltro ti è già stato detto sopra)....ovvero:
$logx<-1/2$
e
$0
ora tiriamo fuori anche la condizione iniziale dal cassetto, risolviamo in x i due intervalli trovati ed otteniamo la soluzione
$(0
fine
La disequazione è di una banalità imbarazzante (per uno che ha come obiettivo un esame di Analisi all'Università). Quindi, il consiglio che ti posso dare è abbandonare gli esercizi e metterti a studiare profondamente la teoria.....poi ovviamente fai ciò che ti pare e che ritieni più opportuno.
Testo[nota]anche se si tratta di logaritmi naturali viene più comodo usare sempre la notazione $log$...tanto si usano sempre quelli...[/nota]:
$2logx-3<(2logx+3)/(logx)$
La PRIMA COSA DA FARE....e che non hai fatto, se non solo parzialmente ed alla fine... è indicare le condizioni di esistenza....ovvero
${{: ( x>0 ),( x !=1 ) :}$
fatto questo (mettiamo la condizione nel cassetto e la tireremo fuori alla fine....)
non servono tutti quei passaggi che continui a fare ogni volta (senza peraltro ragionare sul problema) ma si porta tutto al membro di sinistra così, facendo come sempre il mcm e sommando i vari addendi:
$(2log^2 x-5logx-3)/(logx)<0$
(nota che non ho eliminato il denominatore perché è una disequazione....)
ora studiamo separatamente il segno del numeratore e del denominatore[nota]indico con la riga continua l'intervallo dove il numeratore (N) oppure il denominatore (D) risultano maggiori di zero mentre con quella tratteggiata dove essi risultano minori di zero[/nota]:
(click per ingrandire)
ora vedi bene che, affinché il rapporto sia minore di zero, i due intervalli in cui la disequazione è verificata sono quelli dove ci ho messo la freccia (come peraltro ti è già stato detto sopra)....ovvero:
$logx<-1/2$
e
$0
ora tiriamo fuori anche la condizione iniziale dal cassetto, risolviamo in x i due intervalli trovati ed otteniamo la soluzione
$(0
fine
tommik seguirò sicuramente i tuoi consigli. Il problema è che ho abbandonato da diversi anni (più di 20 ormai) la materia e sto cercando di riprendere, non senza qualche difficoltà (in primis il tempo a disposizione). Quello che per voi può essere banale, per me non lo è, ma non mollo. 


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo