Calcolo derivata
Ciao a tutti, non riesco a calcolare questa derivata prima:
$y=(6x+4)(1-x^3)$
io ho fatto così: $y'=6(1-x^3)+(6x+4)(-3x^2)$ ---->$y'=6-6x^3+(-18x^3-12x^2)$ ----->$y'=-24x^3-12x^2+6$
che infatti è lo stesso risultato che mi danno tutti i calcolatori di derivate online. ad es.: https://www.wolframalpha.com/input/?i=d ... 1-x%5E3%29
ovviamente ho applicato la formula (regola di derivazione): $y = f(x) ∙ g(x) = f'(x) ∙ g(x) + g'(x) ∙ f(x)$
Invece sul libro mi esce un altro risultato:
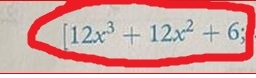
$y=(6x+4)(1-x^3)$
io ho fatto così: $y'=6(1-x^3)+(6x+4)(-3x^2)$ ---->$y'=6-6x^3+(-18x^3-12x^2)$ ----->$y'=-24x^3-12x^2+6$
che infatti è lo stesso risultato che mi danno tutti i calcolatori di derivate online. ad es.: https://www.wolframalpha.com/input/?i=d ... 1-x%5E3%29
ovviamente ho applicato la formula (regola di derivazione): $y = f(x) ∙ g(x) = f'(x) ∙ g(x) + g'(x) ∙ f(x)$
Invece sul libro mi esce un altro risultato:
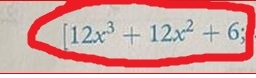
Risposte
Sei sicuro di aver scritto correttamente il testo?
La soluzione del libro è la derivata di $ y=(6x+4)(1+x^3) $,
quella che hai scritto tu è correttamente quella di $ y=(6x+4)(1-x^3) $
La soluzione del libro è la derivata di $ y=(6x+4)(1+x^3) $,
quella che hai scritto tu è correttamente quella di $ y=(6x+4)(1-x^3) $
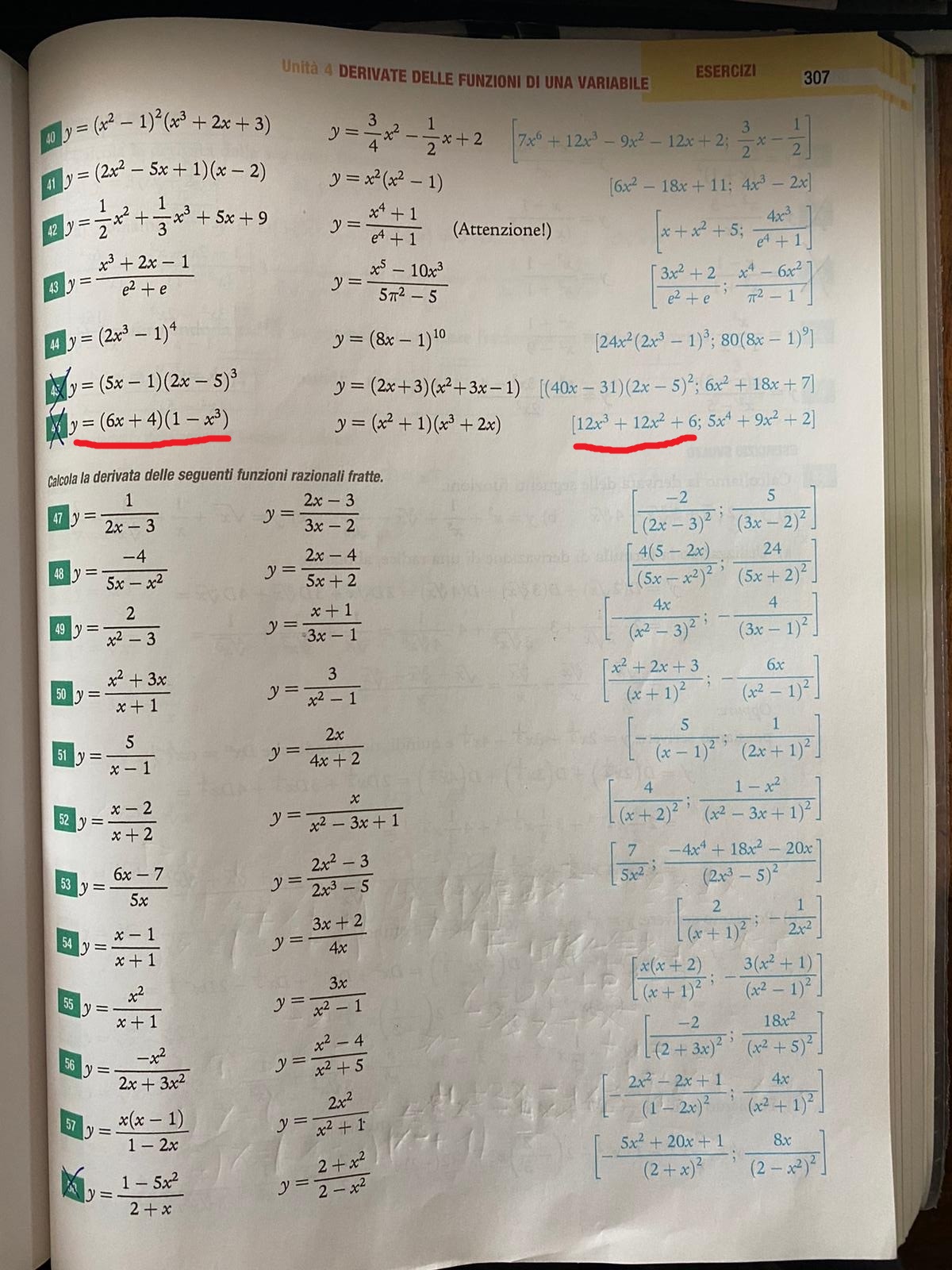
ciao, grazie per la risposta. ti posto direttamente la foto del libro (sottolineato in rosso):

Facciamo la controprova facendo il prodotto, tanto per completezza.
$f(x)=(6x+4)(1-x^3)=6x+4-6x^4-4x^3=-6x^4-4x^3+6x+4$
da cui $f'(x)=-24x^3-12x^2+6$
Perché l'ho fatto visto che ci eravate arrivati? Beh, anche per esercizio personale.
$f(x)=(6x+4)(1-x^3)=6x+4-6x^4-4x^3=-6x^4-4x^3+6x+4$
da cui $f'(x)=-24x^3-12x^2+6$
Perché l'ho fatto visto che ci eravate arrivati? Beh, anche per esercizio personale.
cheppalle sti errori nei libri di matematica...ne ho già trovati diversi su vari testi...non li sopporto


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo