Aiuto urgente sistema parabola retta scuola superiori

[dolalala04]

ciao! scusatemi se vi stresso, ma io e le parabole non andiamo d'accordo... qualcuno potrebbe spiegarmi e\o svolgermi questo esercizio? si tratta di un sistema parabola retta.
l'esercizio chiede di rappresentare algebricamente e graficamente il seguente sistema..
Y= x alla seconda + 2x -1
e parallela alla retta di equazione 2x + y +1 =0

[Yuri.Nardi]

ciao dolalala04 ,

se vuoi ti faccio un richiamo alla teoria della parabola:
definizione di parabola: e' l luogo geometrico dei punti del piano equidistanti da un punto fisso detto fuoco e da una retta detta direttrice.

l'espressione generalizzata della parabola:
Y=a*X^2+b*X+c
dove a,b e c sono dei coefficienti che possono essere costanti o parametrici.
osservazione 1:
se a e' positiva, allora la parabola e' rivolta verso l'alto
se a e' negativa, allora la parabola e' rivolta verso il basso

la parabola puo' anche essere rivolta verso destra o verso sinistra ma a quel punto non si tratta piu' di una funzione dato che per ogni X si associano due distinte Y e si esprime come:
X=a*Y^2+b*Y+c

tornando alla definizione di parabola e all'espressione della funzione generalizzata in X, ci sono elementi geometrici notevoli che la caratterizzano:
1)fuoco: F=(-b/(2*a);(1-(b^2-4*a*c))/(4*a))
2)vertice: V=(-b/(2*a);-(b^2-4*a*c)/(4*a))
3)direttrice: y=-(1+(b^2-4*a*c))/(4*a))
4)asse di simmetria: X=-b/(2*a)

passando all'esercizio, nella rappresentazione delle due funzioni rappresentiamo tutte le proprieta' della parabola (anche se non tutte sono necessarie per la sua rappresentazione grafica) e rappresentiamo la retta (soprattutto u punti di intersezione con la parabola)

le due funzioni sono:
(parabola) Y=X^2+2*X-1
(retta) Y=-2*X-1

a=1
b=2
c=-1

che se sostituite nelle definizioni si ha:
F(-1,-7/4)
V(-1,-2)
y=-9/4 (direttrice)
x=-1 (asse di simmetria)

zeri della parabola per la rappresentazione grafica (ricordo che sqrt[argomento] indica la radice quadrata dell'argomento):
X^2+2*X-1=0
X1=-1+sqrt[2] (punto A(-1+sqrt[2],0))
X2=-1-sqrt[2] (punto B(-1-sqrt[2],0))

punti di intersezione della parabola con la retta (sono 2 , M e N):
X^2+2*X-1=-2*X-1
che risolvendo restituisce 2 risultati:
M(-4,7)
N(0,-1)


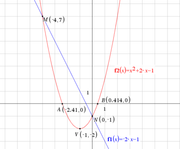
le parallele alla retta Y=-2*X-1 e' un fascio di rette che hanno tutte la stessa pendenza:
Y=-2*X+q

se intersechiamo la parabola con il fascio di rette, ricavo una infinita coppia di punti. I due punti collasseranno in un'unico punto per la retta del fascio tangente alla parabola:
X^2+2*X-1=-2*X+q
che risolvendo:
X1=-2+sqrt[q+5]
X2=-2-sqrt[q+5]

sostituendo X1 e X2 nell'equazione della parabola ricavo la generica coppia di punti:
K(-2+sqrt[q+5],-2*sqrt[q+5]+q+4)
Q(-2-sqrt[q+5],2*sqrt[q+5]+q+4)


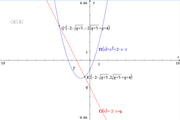
la retta del fascio tangente alla parabola si ricava imponendo X1=X2:
-2+sqrt[q+5]=-2-sqrt[q+5]
q=-5 (che e' anche la q minima possibile)
Y=-2*X-5

punto di tangenza:
T(-2,-1)


Buona esercitazione :D