Salve a tutti mi potete aiutare con un problema di geometria per favore

[12aby]

Calcola il perimetro di un trapezio isoscele sapendo che la somma e la differenza delle basi sono rispettivamente 160 dm e 44 dm e che il lato obliquo é 1/3 della base maggiore.

La risposa deve essere 228 dm
Grazie a tutti buone vacanze

[tiscali]

Ciao, 12aby!

C'è qualcosa in particolare che non hai capito del problema?

[12aby]

Ciao tiscali non ho capito bene come iniziare il problema e che cosa fare con il 1/3 del lato obliquo
Mi puoi aiutare

[tiscali]

Allora, anzitutto inserisco un'immagine del trapezio isoscele, in modo che possa spiegarti più agevolmente i vari procedimenti:




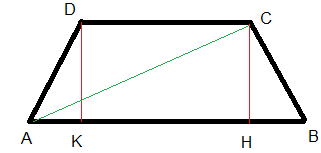
Abbiamo le due basi, maggiore e minore (rispettivamente AB e DC). La loro somma e la loro differenza misurano rispettivamente 160 dm e 44 dm. Uno dei due lati obliqui, poniamo AD, è

[math]\frac{1}{3}[/math]

di AB. Ora, conoscendo la somma e la differenza tra le due basi, possiamo facilmente calcolare le loro dimensioni con una semplice operazione:

[math]AB = \frac{(AB + DC) + (AB - DC)}{2} = \frac{160 + 44}{2} = \frac{204}{2} = 102 dm[/math]

[math]DC = \frac{(AB + DC) - (AB - DC)}{2} = \frac{160 - 44}{2} = 58 dm[/math]

Ora, poiché il lato obliquo è pari a

[math]\frac{1}{3}[/math]

di AB, possiamo determinare la sua misura dividendo semplicemente per 3 la base maggiore:

[math]AD = \frac{AB}{3} \to \frac{102}{3} = 34 dm[/math]

Possiamo procedere col calcolo del perimetro:


P = AB + DC + AD + CB = 102 + 58 + 34 + 34 = 228 dm



Spero sia tutto chiaro.

[12aby]

Grazie Tiscali per tutto e la spiegazione