Variabile aleatoria con pdf nota

[MrEngineer]

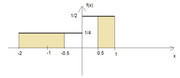
Sia $X$ una variabile aleatoria la cui pdf è quella in figura:

Sia inoltre $Y = X^2$. Determinare:
1) il valore atteso di $X$;
2) la varianza di $X$;
3) la probabilità che $|X| > 0.5$;
4) la media di $Y$;
5) la probabilità che $Y > 0$.

[Risoluzione]

Innanzitutto per calcolare il valore di $k$ tengo conto del fatto che:

$ int_(-oo)^(+oo) f_x (x) dx = 1 $ da cui si ottiene $k = 1/4$.
1) Noto il valore di $k$ trovo tramite definizione che il valore medio $\eta_x = -1/4$;

2) Trovo che la varianza $\sigma_x^2 = 37/48$;

3) $|X| > 0.5$ equivale a dire $x < -0.5 \vee x > 0.5$. Tutto questo si traduce nella probabilità $P(x < -1/2 \vee x>1/2)$ = $ int_(-2)^(-1/2) f_X(x) dx + [1 - int_(-2)^(1/2)f_X(x)dx] $ ???

[Lo_zio_Tom]

prima che butti tanto tempo nell'esercizio (che definire banale è già una sopravvalutazione) ti faccio notare che

- per il punto 1) bastava imporre le aree dei rettangoli pari a uno: $2k+2k=1 rarr k=1/4$

- per il punto 3) idem con patate...è il valore delle aree colorate: $mathbb{P}[|X|>0.5]=1/2*1/2+3/2*1/4=5/8$




- per i valori di sintesi di $Y=X^2$ non serve calcolare la pdf di $Y$ ma basta ricordare, ad esempio, che $mathbb{E}[Y]=int_mathcal(D)x^2f(x)dx$
(e quindi se hai calcolato la varianza[nota]della quale non ho controllato la correttezza del risultato[/nota] hai anche già calcolato la media di $Y$)

- il punto 5) è fantastico.....ti chiede la probabilità che $X^2$ sia maggiore di zero....

[MrEngineer]

sisi lo so per carità scomodare gli integrali per calcolare l'area di un rettangolino è superfluo ma l'ho fatto solo per capirci meglio e riportare le definizioni precise.

Avrei solo una domanda un pò stupida sul punto 3. L'area del rettangolino di sinistra che hai colorato è ok, l'area del rettangolino di destra inizialmente l'avevo pensata anche io. Tuttavia, ho scritto (credo, forse) una stupidaggine perchè, se la cdf rappresenta la probabilità che $X<=x$ e se la cdf stessa è l'integrale della pdf, in questo caso $P(X>1/2)$ non equivale a dire $1 - P(X<1/2)$?

Edit: ho calcolato sia tramite il complementare $1-P(X<1/2)$ sia tramite le aree dei rettangolini che mi hai gentilmente fornito e confermo il risultato di $5/8$.

Potevo quindi considerare direttamente anche l'area del rettangolo di base $|1-1/2|$ e altezza $2k$??

4) la media di $Y$ risulta pari a $5/6$ (che, se i miei calcoli sono corretti, sarebbe il valore quadratico medio della variabile $X$).

5) la probabilità che $Y>0$ vale $1$ tranne se $X = 0$???