Trasformazione variabile aleatoria uniforme
Scusami se continuo in questo topic, ma non mi sembra il caso di aprirne un altro, vorrei solo fare una domanda veloce.Il testo dell'esercizio è:
Se $X$ è la variabile aleatoria uniforme sull'intervallo [-1,2], caratterizzare la variabile aleatoria $Y=|X|$ e disegnare il grafico della sua funzione di densità di probabilità.
Cosa intende con "caratterizzare la variabile aleatoria" ?
Se $X$ è la variabile aleatoria uniforme sull'intervallo [-1,2], caratterizzare la variabile aleatoria $Y=|X|$ e disegnare il grafico della sua funzione di densità di probabilità.
Cosa intende con "caratterizzare la variabile aleatoria" ?
Risposte
a me invece pare proprio il caso. Ogni esercizio vuole un topic a sé. Non è una mia fisima ma serve per tenere in ordine la stanza. Gli esercizi che postate, una volta risolti, rimangono come know-how di tutti; inserendo un topic ogni esercizio se ne facilita la ricerca, mentre mettere più esercizi in un topic unico non fa altro che aumentare la confusione....e poi a me piace di più così, e dato che la Stanza la gestisco io.....cortesemente fate come dico io..... 
Ciò premesso, ti sta chiedendo di calcolare la distribuzione della nuova variabile aleatoria.
PS: usare la formuletta del Gelli va bene, ma anche un pizzico di ragionamento non guasterebbe....
a conti fatti, la CDF della nuova variabile ti dovrebbe venire così:
$F_Y(y)={{: ( 0 , ;y<0),( 2/3y , ;0<=y<1 ),( (y+1)/3 ,;1<=y<2 ),( 1 , ;y>=2 ) :}$
Ciò premesso, ti sta chiedendo di calcolare la distribuzione della nuova variabile aleatoria.
PS: usare la formuletta del Gelli va bene, ma anche un pizzico di ragionamento non guasterebbe....
a conti fatti, la CDF della nuova variabile ti dovrebbe venire così:
$F_Y(y)={{: ( 0 , ;y<0),( 2/3y , ;0<=y<1 ),( (y+1)/3 ,;1<=y<2 ),( 1 , ;y>=2 ) :}$
Va bene scusami per l'errore, credevo fosse superfluo aprirne un altro  .
.
Con distribuzione della nuova variabile aleatoria intendi la sua CDF (funzione di distribuzione cumulativa)?
 .
.Con distribuzione della nuova variabile aleatoria intendi la sua CDF (funzione di distribuzione cumulativa)?
Potresti mostrarmi in che modo l'hai risolto?
mmhhh si dai....ma per spiegarlo devo fare un grafico...attendi qualche minuto (è più lungo da spiegare che da fare....)
Prima di tutto disegni il grafico della funzione di Trasformazione
(cliccami per ingrandirmi)
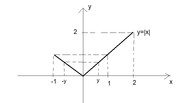
la prima cosa da osservare è che il supporto della variabile $Y$ (l'immagine della funzione di trasformazione) è $S_Y in [0;2]$
ma come vedi, nell'intervallo $y in [0;1]$ la trasformazione non è monotona mentre nell'intervallo residuo la distribuzione della $Y$ è la stessa di quella della $X$ (lì la trasformazione è $Y=X$)
ora per la parte non monotona usando la definzione di CDF hai che
$F_Y(y)=mathbb{P}[Y<=y]=mathbb{P}[-y<=X<=y]=F_X(y)-F_X(-y)=(y+1)/3-(-y+1)/3=2/3y$
dato che la $X$ è una uniforme in $[-1;2]$ e quindi ha come CDF la seguente $F_X(x)=(x+1)/3$
fine.
PS: se usi la funzione "cerca" troverai centinaia e centinaia di esercizi sulle trasformazioni (alcuni anche molto articolati) in questo forum, tutti completamente risolti e commentati (diverse centinaia da me)
Prima di tutto disegni il grafico della funzione di Trasformazione
(cliccami per ingrandirmi)

la prima cosa da osservare è che il supporto della variabile $Y$ (l'immagine della funzione di trasformazione) è $S_Y in [0;2]$
ma come vedi, nell'intervallo $y in [0;1]$ la trasformazione non è monotona mentre nell'intervallo residuo la distribuzione della $Y$ è la stessa di quella della $X$ (lì la trasformazione è $Y=X$)
ora per la parte non monotona usando la definzione di CDF hai che
$F_Y(y)=mathbb{P}[Y<=y]=mathbb{P}[-y<=X<=y]=F_X(y)-F_X(-y)=(y+1)/3-(-y+1)/3=2/3y$
dato che la $X$ è una uniforme in $[-1;2]$ e quindi ha come CDF la seguente $F_X(x)=(x+1)/3$
fine.
PS: se usi la funzione "cerca" troverai centinaia e centinaia di esercizi sulle trasformazioni (alcuni anche molto articolati) in questo forum, tutti completamente risolti e commentati (diverse centinaia da me)
Con il tuo ragionamento mi risulta abbastanza chiaro.. ho provato invece a utilizzare la solita formula per il calcolo della pdf della variabile aletoria $Y$ ma mi sto perdendo tra i calcoli.
Come al solito ho $f_{Y}(y)=\sum_{i} f_{X}(x_{i})/|g'(x_{i})|$. Allora risolvo l'equazione $y = |x|$ ottenendo
$x=-y$ se $y<0$ , $x=y$ se $y>0$. Inoltre $|g'(x)|=1$. Allora sia per $y>0$ che per $y<0$ ho che $f_{Y}(y)=f_{X}(x_{i})$ cioè
$f_{Y}(y)= 1/3$ se $y$ o $-y$ $in [-1,2]$, $f_{Y}(y)= 0$ altrove. Ovviamente questo risultato è sbagliato. Dove commetto l'errore procedendo in questo modo?
Come al solito ho $f_{Y}(y)=\sum_{i} f_{X}(x_{i})/|g'(x_{i})|$. Allora risolvo l'equazione $y = |x|$ ottenendo
$x=-y$ se $y<0$ , $x=y$ se $y>0$. Inoltre $|g'(x)|=1$. Allora sia per $y>0$ che per $y<0$ ho che $f_{Y}(y)=f_{X}(x_{i})$ cioè
$f_{Y}(y)= 1/3$ se $y$ o $-y$ $in [-1,2]$, $f_{Y}(y)= 0$ altrove. Ovviamente questo risultato è sbagliato. Dove commetto l'errore procedendo in questo modo?


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo