Statistica campionaria e media campionaria
Ciao a tutti,
non capisco un concetto teorico che riguarda la media campionaria.
Riporto il testo nello spazio sottostante, al seguito del quale esporrò i miei dubbi.
Consiglio di leggere il Nota-Bene in fondo prima di rispondere.
" - Data una popolazione $H$ costituita da individui adulti, è possibile considerare una qualsiasi grandezza numerica di interesse, come reddito annuale, statura, età, ecc.
-Siano $X_1, X_2, ... , X_n$ un campione di dati estratto da questa popolazione.
-I valori numerici associati a ciascuno degli elementi del campione sono variabili aleatorie indipendenti ed identicamente distribuite.
-Denotiamo con $mu$ la media e con $sigma^2$ la loro varianza.
-Definiamo la media campionaria come $bar(X)= 1/n sum_i (X_i)$"
Domande
1) Non riesco a capire, nella pratica, chi siano i vari $X_1, X_2, ..., X_n$.
Fino ad ora ero stato abituato a chiamare con tali nomi le variabili aleatorie, quindi ad esempio
$X_1 =$ numero di persone più alte di un metro e ottanta
$X_2=$ numero di persone con età inferiore a 20 anni
ecc.
Ma questo non avrebbe alcun senso perché, nell'applicare la definizione di media campionaria, scriverei
$text(età+statura+...+ecc) /n$
Qualcuno sarebbe in grado di fare un esempio per chiarire questo mio dubbio?
2) "I valori numerici associati a ciascuno degli elementi del campione sono variabili aleatorie indipendenti ed identicamente distribuite."
Come prima: ma i valori numerici non sono semplicemente dati?
Come può il singolo dato, ad esempio
$text(altezza di Pippo)= 1,80m$
essere una variabile aleatoria?
N.B. Questi miei dubbi sono nati dopo che ho letto ciò che è stato scritto sul valore atteso della media campionaria, ovvero
$E[bar(X)]= (E[X_1] + E[X_2] + E[X_3] + ... + E[X_n] )/n$
Come possono i vari $X_i$ essere dei semplici dati, se poi vado a calcolare il valore atteso di $X_i$ ???
Grazie a chiunque sia in grado di aiutarmi
non capisco un concetto teorico che riguarda la media campionaria.
Riporto il testo nello spazio sottostante, al seguito del quale esporrò i miei dubbi.
Consiglio di leggere il Nota-Bene in fondo prima di rispondere.
" - Data una popolazione $H$ costituita da individui adulti, è possibile considerare una qualsiasi grandezza numerica di interesse, come reddito annuale, statura, età, ecc.
-Siano $X_1, X_2, ... , X_n$ un campione di dati estratto da questa popolazione.
-I valori numerici associati a ciascuno degli elementi del campione sono variabili aleatorie indipendenti ed identicamente distribuite.
-Denotiamo con $mu$ la media e con $sigma^2$ la loro varianza.
-Definiamo la media campionaria come $bar(X)= 1/n sum_i (X_i)$"
Domande
1) Non riesco a capire, nella pratica, chi siano i vari $X_1, X_2, ..., X_n$.
Fino ad ora ero stato abituato a chiamare con tali nomi le variabili aleatorie, quindi ad esempio
$X_1 =$ numero di persone più alte di un metro e ottanta
$X_2=$ numero di persone con età inferiore a 20 anni
ecc.
Ma questo non avrebbe alcun senso perché, nell'applicare la definizione di media campionaria, scriverei
$text(età+statura+...+ecc) /n$
Qualcuno sarebbe in grado di fare un esempio per chiarire questo mio dubbio?
2) "I valori numerici associati a ciascuno degli elementi del campione sono variabili aleatorie indipendenti ed identicamente distribuite."
Come prima: ma i valori numerici non sono semplicemente dati?
Come può il singolo dato, ad esempio
$text(altezza di Pippo)= 1,80m$
essere una variabile aleatoria?
N.B. Questi miei dubbi sono nati dopo che ho letto ciò che è stato scritto sul valore atteso della media campionaria, ovvero
$E[bar(X)]= (E[X_1] + E[X_2] + E[X_3] + ... + E[X_n] )/n$
Come possono i vari $X_i$ essere dei semplici dati, se poi vado a calcolare il valore atteso di $X_i$ ???
Grazie a chiunque sia in grado di aiutarmi
Risposte
iniziamo ad entrare nell'Inferenza...secondo me devi passare oltre, studiare un po' poi ne riparliamo....siamo ovviamente qui ad aiutarti.
Tanto per iniziare
Abbiamo una popolazione (una cosa astratta) che si distribuisce in un determinato modo, ad esempio la popolazione è distribuita come una Gaussiana di media ignota e varianza 1.
Vogliamo fare inferenza su quel parametro che non conosciamo. A questo punto facciamo degli esperimenti ed estraiamo un campione casuale. Il campione estratto si chiama
$X_1,...,X_n$
per le ipotesi fatte sul campionamento casuale, ogni $X_i$ ha la stessa distribuzione della popolazione $X$ e tutti gli elementi del campione sono fra loro indipendenti.
Tale campione darà origine ad una determinata realizzazione[nota]di solito si scrive in minuscolo per non confondere il numero con il numero aleatorio[/nota]
$(x_1,...,x_n)$
Questa realizzazione sì è una n-upla numerica.
Sul campione possiamo analizzare alcune funzioni, cioè delle statistiche, ad esempio la media empirica, cioè campionaria: $bar(X)_n=1/n SigmaX$
ed usare il dato ottenuto sulla realizzazione osservata della media empirica per dare delle stime sulla media ignota della popolazione
ecc ecc
Hai ragione....i vari $X_i$ sono tutti numeri aleatori tramite i quali si calcolano "stimatori" che avranno una loro manifestazione numerica (stima)
^^^^^^^^^^^^^^^^^
Esempio:
Consideriamo la produzione di viti di un certo diametro da un certo macchinario. E' noto (supponiamo) che il diametro delle viti ha una distribuzione normale di media $mu$ e varianza $sigma^2$.
Nessuno conoscerà mai il diametro esatto delle viti perché tale diametro varia, magari anche di pochissimo, ma varia.
Questa è la popolazione $X~N(mu;sigma^2)$
per capirci qualche cosa estraiamo un campione casuale di $n$ viti prodotte, ad esempio 1000 viti.
Per le ipotesi fatte (che vanno opportunamente definite con apposite procedure sul campionamento casuale affinché siano soddisfatte) il diametro di ogni vite estratta sarà una variabile casuale ed avrà la stessa distirbuzione $X_i~N(mu;sigma^2)$; inoltre tutte le $X_i$ sono fra loro stocasticamente indipendenti.
Facendo dei ragionamenti su alcune funzioni campionarie[nota]che sono anche loro variabili aleatorie, essendo funzioni di $n$ numeri aleatori[/nota], ad esempio media e varianza campionarie, $bar(X)_n$ e $S_n^2$ si posso ottenere informazioni utili per avere una stima sui parametri ignoti.
Quindi il campione casuale $(X_1,....,X_1000)$ è una n-upla di numeri (aleatori). Tali numeri avranno la loro manifestazione numerica che darà origine ad una stima (un numero) che usiamo per validare determinate ipotesi fatte a priori, ad esempio, sul vero diametro delle viti prodotte.
^^^^^^^^^^^^^^^^^
Ti cerco un'ottima dispensa davvero ben fatta che ti chiarirà tutto
EDIT:
questa
E' un riassunto fatto davvero molto bene...
Tanto per iniziare
Abbiamo una popolazione (una cosa astratta) che si distribuisce in un determinato modo, ad esempio la popolazione è distribuita come una Gaussiana di media ignota e varianza 1.
Vogliamo fare inferenza su quel parametro che non conosciamo. A questo punto facciamo degli esperimenti ed estraiamo un campione casuale. Il campione estratto si chiama
$X_1,...,X_n$
per le ipotesi fatte sul campionamento casuale, ogni $X_i$ ha la stessa distribuzione della popolazione $X$ e tutti gli elementi del campione sono fra loro indipendenti.
Tale campione darà origine ad una determinata realizzazione[nota]di solito si scrive in minuscolo per non confondere il numero con il numero aleatorio[/nota]
$(x_1,...,x_n)$
Questa realizzazione sì è una n-upla numerica.
Sul campione possiamo analizzare alcune funzioni, cioè delle statistiche, ad esempio la media empirica, cioè campionaria: $bar(X)_n=1/n SigmaX$
ed usare il dato ottenuto sulla realizzazione osservata della media empirica per dare delle stime sulla media ignota della popolazione
ecc ecc
"anonymous_58f0ac":
Come possono i vari $X_i$ essere dei semplici dati, se poi vado a calcolare il valore atteso di $X_i$ ???
Hai ragione....i vari $X_i$ sono tutti numeri aleatori tramite i quali si calcolano "stimatori" che avranno una loro manifestazione numerica (stima)
^^^^^^^^^^^^^^^^^
Esempio:
Consideriamo la produzione di viti di un certo diametro da un certo macchinario. E' noto (supponiamo) che il diametro delle viti ha una distribuzione normale di media $mu$ e varianza $sigma^2$.
Nessuno conoscerà mai il diametro esatto delle viti perché tale diametro varia, magari anche di pochissimo, ma varia.
Questa è la popolazione $X~N(mu;sigma^2)$
per capirci qualche cosa estraiamo un campione casuale di $n$ viti prodotte, ad esempio 1000 viti.
Per le ipotesi fatte (che vanno opportunamente definite con apposite procedure sul campionamento casuale affinché siano soddisfatte) il diametro di ogni vite estratta sarà una variabile casuale ed avrà la stessa distirbuzione $X_i~N(mu;sigma^2)$; inoltre tutte le $X_i$ sono fra loro stocasticamente indipendenti.
Facendo dei ragionamenti su alcune funzioni campionarie[nota]che sono anche loro variabili aleatorie, essendo funzioni di $n$ numeri aleatori[/nota], ad esempio media e varianza campionarie, $bar(X)_n$ e $S_n^2$ si posso ottenere informazioni utili per avere una stima sui parametri ignoti.
Quindi il campione casuale $(X_1,....,X_1000)$ è una n-upla di numeri (aleatori). Tali numeri avranno la loro manifestazione numerica che darà origine ad una stima (un numero) che usiamo per validare determinate ipotesi fatte a priori, ad esempio, sul vero diametro delle viti prodotte.
^^^^^^^^^^^^^^^^^
Ti cerco un'ottima dispensa davvero ben fatta che ti chiarirà tutto
EDIT:
questa
E' un riassunto fatto davvero molto bene...
Ti ringrazio innanzitutto per la risposta.
Posto uno screen shot del testo da te consigliato

Osservando la prima equazione penso ciò:
Ma quindi nella statistica campionaria le $X_i $ sono semplicemente i dati e non più delle variabili aleatorie e la media campionaria non è altro che una semplice media aritmetica dei dati?
Mi confermi ciò?
Forse sono un po' arrogante nel pemsare questo, ma mi sembra che le mie perplessità nascono anche a causa della confusione di notazione nella materia.
Posto uno screen shot del testo da te consigliato

Osservando la prima equazione penso ciò:
Ma quindi nella statistica campionaria le $X_i $ sono semplicemente i dati e non più delle variabili aleatorie e la media campionaria non è altro che una semplice media aritmetica dei dati?
Mi confermi ciò?
Forse sono un po' arrogante nel pemsare questo, ma mi sembra che le mie perplessità nascono anche a causa della confusione di notazione nella materia.
ripeto:
La popolazione ha una determinata distribuzione $X~ F_(X)(x)$
nota che ho scritto $X$ maiuscolo al pedice mentre $x$ minuscolo fra parentesi.
Ciò in quanto con la lettera maiuscola si indicano le variabili mentre con la lettera minuscola le REALIZZAZIONI di tali variabili.
Se per ragioni che ora ti sembrano oscure, si estrae un campione casuale da $X$, chiamiamo tale campione
$(X_1,...,X_n)$
questo è un vettore di variabili aleatorie, e tutte le n variabili sono indipendenti ed hanno la stessa distribuzione di $X$
la media campionaria, cioè la media aritmetica di tali variabili, è anch'essa è una variabile, essendo trasfomazione di n variabili aleatorie...
Tutte le variabili avranno le loro manifestazioni numeriche....che indichiamo con le lettere minuscole.
Dato che sei proprio agli inizi è normale essere un po' spiazzato....leggi, studia, fai esercizi e tutto ti si chiarirà. Quella dispensa che ti ho indicato è ricca di considerazioni molti interessanti. Leggila con attenzione.
Ti faccio un semplice esempio
$X~ U(0;1)$
cioè la popolazione è distribuita in modo uniforme in $(0;1)$
Estraiamo un campione casuale di ampiezza $n=2$ ovvero $(X_1,X_2)$ e concentriamoci sulla variabile
$bar(X)=(X_1+X_2)/2$
la media della media campionaria la sai...la varianza della media campionaria pure...ma dovresti essere in grado di calcolare anche la distribuzione di tale variabile "media"
Come vedi la media campionaria è anche lei una distribuzione aleatoria....
cioè il massimo ed il minimo del campione estratto.
Se riuscirai a risolvere questi semplici quesiti ok...altrimenti sotto con lo studio...
La popolazione ha una determinata distribuzione $X~ F_(X)(x)$
nota che ho scritto $X$ maiuscolo al pedice mentre $x$ minuscolo fra parentesi.
Ciò in quanto con la lettera maiuscola si indicano le variabili mentre con la lettera minuscola le REALIZZAZIONI di tali variabili.
Se per ragioni che ora ti sembrano oscure, si estrae un campione casuale da $X$, chiamiamo tale campione
$(X_1,...,X_n)$
questo è un vettore di variabili aleatorie, e tutte le n variabili sono indipendenti ed hanno la stessa distribuzione di $X$
la media campionaria, cioè la media aritmetica di tali variabili, è anch'essa è una variabile, essendo trasfomazione di n variabili aleatorie...
Tutte le variabili avranno le loro manifestazioni numeriche....che indichiamo con le lettere minuscole.
Dato che sei proprio agli inizi è normale essere un po' spiazzato....leggi, studia, fai esercizi e tutto ti si chiarirà. Quella dispensa che ti ho indicato è ricca di considerazioni molti interessanti. Leggila con attenzione.
Ti faccio un semplice esempio
$X~ U(0;1)$
cioè la popolazione è distribuita in modo uniforme in $(0;1)$
Estraiamo un campione casuale di ampiezza $n=2$ ovvero $(X_1,X_2)$ e concentriamoci sulla variabile
$bar(X)=(X_1+X_2)/2$
1) come si distribuisce $bar(X)$?
la media della media campionaria la sai...la varianza della media campionaria pure...ma dovresti essere in grado di calcolare anche la distribuzione di tale variabile "media"
Come vedi la media campionaria è anche lei una distribuzione aleatoria....
2) Fatto questo calcola anche la distribuzione di altre statistiche importantissime[nota]nota che qui, oltre ad usare la lettera maiuscola sia io che il libro abbiamo messo il pedice fra parentesi: ciò significa che le variabili sono ordinate, dalla più piccola alla più grande.[/nota]:
$X_((1))$ e $X_((2))$
cioè il massimo ed il minimo del campione estratto.
3) poi prosegui e calcola la covarianza fra il minimo ed il massimo
Se riuscirai a risolvere questi semplici quesiti ok...altrimenti sotto con lo studio...
Ti ringrazio tommik, leggo la dispensa e forse incominciando a fare esercizi mi sarà effettivamente tutto un pò più chiaro..
Ti chiedo un'ultima cortesia, poi non ti disturbo più :
Mi potresti fare un esempio pratico di questi concetti:
Ti chiedo un'ultima cortesia, poi non ti disturbo più :
Mi potresti fare un esempio pratico di questi concetti:
"tommik":
La popolazione ha una determinata distribuzione $X~ F_(X)(x)$
..
Se per ragioni che ora ti sembrano oscure, si estrae un campione casuale da $X$, chiamiamo tale campione
$(X_1,...,X_n)$
questo è un vettore di variabili aleatorie, e tutte le n variabili sono indipendenti ed hanno la stessa distribuzione di $X$
la media campionaria, cioè la media aritmetica di tali variabili è la media campionaria che anch'essa è una variabile, essendo trasfomazione di n variabili aleatorie...
Tutte le variabili avranno le loro manifestazioni numeriche....che indichiamo con le lettere minuscole.
Certo.
facciamo l'esempio delle viti di prima. Abbiamo delle viti prodotte da una macchina e sappiamo che il diametro (per ragioni ovvie tale diametro non sarà sempre costante ma avrà delle piccolissime variazioni).
Sappiamo che il diametro si distribuisce come una Gaussiana. Indichiamo il diametro con $X$.
Quindi supponiamo ad esempio che $X~ N(mu;1/10)$
Come facciamo ad avere una stima verosimile del corretto diametro delle viti?
1) Estraiamo un campione casuale di viti, ad esempio 10 viti.
Il campione è questo $(X_1,...,X_n)$
2) una importante statistica è la media campionaria che, per ragioni che dovresti sapere, ha la seguente distribuzione
$bar(X)_(10)~ N(mu;1/100)$
In pratica la distribuzione della media è sempre gaussiana, ha la stessa media, cioè ha sempre il massimo in $mu$ ma ha una varianza minore, cioè è una campana più appuntita.
(click sull'immagine per ingrandire)
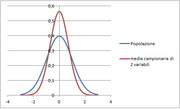
Fatto questo misuriamo i diametri delle viti estratte e troviamo
$(X_1=x_1,...,X_10=x_(10))$
ad esempio misuriamo e troviamo i seguenti valori di diametro
$(5.08;4.98;...5.05)$
calcoliamo la media campionaria e diamo una stima ragionevole del diametro, es $5$
^^^^^^^^^^^^^
Te ne faccio un altro... ma la cosa migliore è aprire i libri e studiare bene la teoria, così parliamo entrambi la stessa lingua.
Facciamo il seguente gioco: tiriamo una moneta regolare, se esce testa vinci 1€ se viene croce perdi 1€.
La variabile X che indica il tuo guadagno è questa
$X={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
se giochiamo due volte, ogni giocata è una variabile aleatoria con la stessa distribuzione della popolazione ed ogni giocata è indipendente dall'altra; in formule
$X_1={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
$X_2={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
La media campionaria (la media aritmetica delle due variabili) guadagno avrà la seguente distribuzione
$bar(X)_2={{: ( -1 , 0,1 ),( 1/4 , 2/4,1/4) :}$
come vedi anche la media campionaria è un numero aleatorio....con la stessa media della popolazione ma varianza minore (la metà, in questo caso)
Quando avrai giocato le due partite, tutti i numeri aleatori ($X_1$, $X_2$ e la loro media aritmetica) avranno le loro realizzazioni, ad esempio
$ul(X)={-1;-1}$
$bar(X)_2=-1$
ma la realizzazione (il numero) è solo una delle possibili realizzazioni del numero aleatorio
^^^^^^^^^^^^^
Si è No.
1) NO, i Dati, visti come elementi del campione aleaorio, SONO variabili aleatorie, i.i.d. con la stessa distribuzione della popolazione. La "realizzazione" dei dati è invece un numero, ma essa serve solo per passare dallo stimatore alla stima.... e
2) Sì, la media campionaria è semplicemente la loro media aritmetica...cioè una media aritmetica di numeri aleatori, con tutte le conseguenze che dovresti conoscere. Appunto ti ho proposto alcuni semplici esempi di trasformazioni di variabili aleatorie per calcolare la distribuzione di alcune medie campionarie...sarebbe opportuno iniziare da lì....anche se non è un compito proposto dal tuo docente....IMHO
facciamo l'esempio delle viti di prima. Abbiamo delle viti prodotte da una macchina e sappiamo che il diametro (per ragioni ovvie tale diametro non sarà sempre costante ma avrà delle piccolissime variazioni).
Sappiamo che il diametro si distribuisce come una Gaussiana. Indichiamo il diametro con $X$.
Quindi supponiamo ad esempio che $X~ N(mu;1/10)$
Come facciamo ad avere una stima verosimile del corretto diametro delle viti?
1) Estraiamo un campione casuale di viti, ad esempio 10 viti.
Il campione è questo $(X_1,...,X_n)$
2) una importante statistica è la media campionaria che, per ragioni che dovresti sapere, ha la seguente distribuzione
$bar(X)_(10)~ N(mu;1/100)$
In pratica la distribuzione della media è sempre gaussiana, ha la stessa media, cioè ha sempre il massimo in $mu$ ma ha una varianza minore, cioè è una campana più appuntita.
(click sull'immagine per ingrandire)

Fatto questo misuriamo i diametri delle viti estratte e troviamo
$(X_1=x_1,...,X_10=x_(10))$
ad esempio misuriamo e troviamo i seguenti valori di diametro
$(5.08;4.98;...5.05)$
calcoliamo la media campionaria e diamo una stima ragionevole del diametro, es $5$
^^^^^^^^^^^^^
Te ne faccio un altro... ma la cosa migliore è aprire i libri e studiare bene la teoria, così parliamo entrambi la stessa lingua.
Facciamo il seguente gioco: tiriamo una moneta regolare, se esce testa vinci 1€ se viene croce perdi 1€.
La variabile X che indica il tuo guadagno è questa
$X={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
se giochiamo due volte, ogni giocata è una variabile aleatoria con la stessa distribuzione della popolazione ed ogni giocata è indipendente dall'altra; in formule
$X_1={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
$X_2={{: ( -1 , 1 ),( 1/2 , 1/2) :}$
La media campionaria (la media aritmetica delle due variabili) guadagno avrà la seguente distribuzione
$bar(X)_2={{: ( -1 , 0,1 ),( 1/4 , 2/4,1/4) :}$
come vedi anche la media campionaria è un numero aleatorio....con la stessa media della popolazione ma varianza minore (la metà, in questo caso)
Quando avrai giocato le due partite, tutti i numeri aleatori ($X_1$, $X_2$ e la loro media aritmetica) avranno le loro realizzazioni, ad esempio
$ul(X)={-1;-1}$
$bar(X)_2=-1$
ma la realizzazione (il numero) è solo una delle possibili realizzazioni del numero aleatorio
^^^^^^^^^^^^^
"anonymous_58f0ac":
Ma quindi nella statistica campionaria le $X_i $ sono semplicemente i dati e non più delle variabili aleatorie e la media campionaria non è altro che una semplice media aritmetica dei dati?
Mi confermi ciò?
Si è No.
1) NO, i Dati, visti come elementi del campione aleaorio, SONO variabili aleatorie, i.i.d. con la stessa distribuzione della popolazione. La "realizzazione" dei dati è invece un numero, ma essa serve solo per passare dallo stimatore alla stima.... e
2) Sì, la media campionaria è semplicemente la loro media aritmetica...cioè una media aritmetica di numeri aleatori, con tutte le conseguenze che dovresti conoscere. Appunto ti ho proposto alcuni semplici esempi di trasformazioni di variabili aleatorie per calcolare la distribuzione di alcune medie campionarie...sarebbe opportuno iniziare da lì....anche se non è un compito proposto dal tuo docente....IMHO
Ottimo.
Mi hai fatto capire alcuni concetti e soprattutto mi hai fatto capire in modo ancora più marcato cosa avevo mal compreso, quali concetti devo approfondire e comprendere meglio!
Grazie mille tommik
Mi hai fatto capire alcuni concetti e soprattutto mi hai fatto capire in modo ancora più marcato cosa avevo mal compreso, quali concetti devo approfondire e comprendere meglio!
Grazie mille tommik
"Sergio":
Nel campionamento da popolazioni teoriche, detto anche campionamento da variabili aleatorie, segui i seguenti passi (l'ultimo è sintetizzato alquanto, ma capire gli altri, soprattutto i primi due, è fondamentale):
1) assumi che il fenomeno d'interesse abbia una certa distribuzione di probabilità; ad esempio, nel lancio di una moneta assumi che si tratti di una distribuzione bernoulliana; formalmente, definisci il modello probabilistico $\{\chi, f_X(x;\theta), \Theta\}$ dove, nel caso di una bernoulliana:
-- $\chi$ è insieme dei valori che la v.a. può assumere, $\chi=\{0,1\}$;
-- $f_X(x;\theta)$ è la distribuzione di probabilità della variabile aleatoria, $\theta^x(1-\theta)^{1-x}$ (con $x in \chi$);
-- $\Theta$ è lo spazio dei parametri, l'insieme dei valori che il parametro può assumere, $\Theta=[0,1]$;
2) definisci il campione casuale come una $n$-upla di variabili aleatorie indipendenti e identicamente distribuite; ad esempio prendi i lanci di $n$ monete o $n$ lanci della stessa moneta e supponi di avere a che fare con $n$ variabili aleatorie bernoulliane; ottieni così il modello statistico che nel caso di $n$ lanci di una moneta è $\{\chi^n; f_n(x_n;\theta)=\prod_{i=1}^n f_X(x_i;\theta); \Theta\}$ dove:
-- $\chi^n=\{0,1\}\times\{0,1\}\times ... \times\{0,1\}=\{0,1\}^n$;
-- $f_n(x_n;\theta)=\prod_{i=1}^n f_X(x_i;\theta)=\prod_{i=1}^n \theta^x(1-\theta)^{1-x}=\theta^{\sum_i x_i}(1-\theta)^{n-\sum_i x_i}$;
-- $\Theta$ è ancora $[0,1]$;
3) definisci statistiche campionarie, che sono funzioni \(\chi^n \to \mathcal{T}\), con \(\mathcal{T}\subset\mathbb{R}^k, k\ge 1\); tra esse la media campionaria. Nel fare questo ragioni solo sulle $n$ variabili aleatorie;
4) guardi i valori osservati e cerchi di capire fino a che punto questi "si avvicinano" a quelli teorici, ad esempio quanto 4 teste in 10 lanci è coerente con la media campionaria se $\theta=0.5$ (moneta regolare).
Il punto fondamentale è che non ragioni su una popolazione che non esiste, ma su variabili aleatorie.
Mi intrometto nel post, spero di non dare fastidio (ciao tauto!)
Due domandine:
a) Sbaglio nel dire che fino al punto 2 sembra lo studio di una binomiale?
b) A cosa servono le funzioni "statistiche campionarie"? Ho provato a leggere dai miei libri di testo ma devo ammettere che mi appare tutto oscuro.
"CLaudio Nine":
b) A cosa servono le funzioni "statistiche campionarie"? Ho provato a leggere dai miei libri di testo ma devo ammettere che mi appare tutto oscuro.
te lo spiego io...
Problema: Abbiamo un'urna che contiene palline bianche e nere ma non sappiamo in che proporzione. Dobbiamo stimare la percentuale di palline bianche.
Come facciamo?
Ci sono molti modi di procedere (io poi sono di formazione bayesiana quindi non farei come sto scrivendo ora) ma per ciò che ti serve quello che scrivo adesso ti basta e ti avanza.
1) Definiamo un modello statistico adeguato. Molto naturalmente il modello è questo
$p(X|theta)=theta^x(1-theta)^(1-x)$
$x=0,1$
$0
Ho scelto un modello bernulliano: quando si estrae una pallina bianca $x=1$ quando si estrae la pallina nera $x=0$.
Devo però capire quanto vale il parametro $theta$
2) Si fa quindi un esperimento che consiste nell'estrarre un certo numero di palline, es 10 e rimettendo ogni volta la pallina estratta nell'urna.
Supponiamo di ottenere la seguente realizzazione campionaria
${0;0;0;0;1;1;0;1;0;1}$
3) Stimo quindi il parametro ignoto $theta$ utilizzando la statistica campionaria $bar(X)_10$ ottenendo una stima del parametro ignoto
$hat(theta)=(0+0+0+0+1+1+0+1+0+1)/10=0.4=40%$
Conclusione: l'urna ha il 40% di palline bianche ed il 60% di palline nere
Osservazione 1
La stima trovata è giusta o sbagliata? La risposta sta nel seguente detto: "se vuoi fare sicuramente un errore, allora fai una stima". Quindi la risposta è che la % trovata è sicuramente sbagliata. Ciò che si deve fare in statistica è ragionare in modo da commettere un errore che, mediamente, è sicuramente più piccolo di ogni altro modo di ragionare.
Osservazione 2
La stima è bella è brutta ce ne saranno di migliori, come devo fare a campionare, quanto deve essere grande il campione, siamo sicuri che queste tecniche statistica classica dia stime attendibili o forse è meglio ragionare in termini bayesiani dove il principio di verosimiglianza è sicuramente rispettato ecc ecc....sono cose che per ora non ti interessano ma sono quesiti a cui per rispondere servono almeno 5 esami di statistica...
"Sergio":
Scusa tommik, ma mi piaceva di più l'esempio delle viti
de gustibus. Secondo me l'esempio dell'urna è perfetto per spiegare a cosa serve la media campionaria. L'ho anche messo per ultimo perché ci ho pensato parecchio. Se vogliamo discutere delle tecniche migliori per stimare quante palline bianche ci sono nell'urna potremmo scrivere pagine e pagine ma non mi pare questa la sede opportuna, anche perché l'esempio dell'urna è solo un esempio per spiegare che stiamo stimando il parametro di un modello di base bernulliano adottando un sistema di campionamento bernulliano
Aspettiamo che l'utente legga e decida lui...se dopo aver letto l'esempio ha avuto una risposta soddisfacente alla domanda posta
"CLaudio Nine":
b) A cosa servono le funzioni "statistiche campionarie"? Ho provato a leggere dai miei libri di testo ma devo ammettere che mi appare tutto oscuro.
allora l'obiettivo del thread è stato raggiunto altrimenti no.
Per il resto ci sono i libri e tanto tanto studio....e non è nemmeno detto che anche dopo tanto studio ci troviamo d'accordo.
La media campionaria come variabile aleatoria "sta dietro al costrutto teorico" secondo il quale si arriva a dire che quella variabile aleatoria è lo stimatore ottimo in un determinato senso.
La media osservata serve per avere la stima del parametro, ovviamente.
La media osservata serve per avere la stima del parametro, ovviamente.
@tommik:
"tommik":
[quote="CLaudio Nine"]
b) A cosa servono le funzioni "statistiche campionarie"? Ho provato a leggere dai miei libri di testo ma devo ammettere che mi appare tutto oscuro.
te lo spiego io...
...
1) Definiamo un modello statistico adeguato.
...
Devo però capire quanto vale il parametro $theta$
2) Si fa quindi un esperimento che consiste nell'estrarre un certo numero di palline
...
3) Stimo quindi il parametro ignoto $theta$ utilizzando la statistica campionaria $bar(X)_10$ ottenendo una stima del parametro ignoto
...
[/quote]
Okay quindi la statistica campionaria è semplicemente una funzione che mi permette di dedurre i parametri di interesse relativi al modello statistico che presumo governi il fenomeno di interesse!
In questo caso ho presunto (ovviamente) un modello statistico bernoulliano.
Il parametro di interesse che non conosco e che voglio stimare grazie all'uso della funzione "statistica campionaria" è $theta$.
In questo caso $theta$ sarà uguale alla probabilità di estrarre una pallina bianca, e, di conseguenza, quante palline bianche ci sono (ovviamente non ragiono in termini di fatti certi ma di stime).
Sei d'accordo tommik?
Sergio ti rispondo subito.
Non posto risposte ma sappiate che sto seguendo il post con moltissimo interesse mentre studio dai libri.
CLaudio Nine condivido molti dei tuoi dubbi.
CLaudio Nine condivido molti dei tuoi dubbi.
@Sergio
"Sergio":
[quote="CLaudio Nine"]a) Sbaglio nel dire che fino al punto 2 sembra lo studio di una binomiale?
Non senti la mancanza del coefficiente binomiale?
[/quote]
Caspita è vero!!
"Sergio":
Definisco invece la media e la statistica campionarie, che sono variabili aleatorie con una loro distribuzione.
Domanda1:
la media campionaria la definisco a priori?
Non faccio altro che definire una variabile aleatoria chiamata media campionaria e a fare un'ipotesi su quella che sarà la sua distribuzione?
Successivamente calcolerò poi quanto sarà probabile che la media campionaria sia lontana dal valor medio?
Domanda2:
prendendo una frase da te scritta, provo a estenderla. Dimmi pure se dico qualche cavolata:
Assumo che il fenomeno segua una qualche distribuzione di probabilità, su questa base e senza guardare i dati definisco statistiche campionarie intese come variabili aleatorie.
Tale funzioni sono utili se non necessarie per definire i parametri di interesse ($theta$ per bernoulliane e binomiali, $lambda$ per esponenziali, $mu$ e $sigma$ per normali, ecc.)
"anonymous_58f0ac":
Non posto risposte ma sappiate che sto seguendo il post con moltissimo interesse mentre studio dai libri.
CLaudio Nine condivido molti dei tuoi dubbi.
Mi fa piacere! Sinceramente avevo sottovalutato questa materia, sono molto pochi i concetti che sono "scontati".
"Sergio":
Sintetizzare un corso di inferenza in poche righe non è semplice. Provo a isolarne il "nocciolo".
Si assume che i dati siano realizzazioni di variabili aleatorie di cui ignoro i parametri. Mi muovo su un piano solo teorico (non mi baso sui dati) per ottenere, passando attraverso una serie di altre variabili aleatorie (statistiche campionarie, ma anche altre), variabili aleatorie che sono trasformazioni delle statistiche campionarie ma di cui conosco i parametri (come la $t$ dell'esempio).
A questo punto, uso le realizzazioni osservate delle statistiche campionarie (ad es. la media osservata) per ottenere realizzazioni di quelle variabili aleatorie di cui conosco i parametri.
In questo modo posso finalmente giungere a conclusioni, ad esempio posso dire quanto è "significativa" una certa differenza tra due temperature medie, ovvero quanto è "credibile" che la differenza sia dovuta solo al caso oppure all'efficacia di un nuovo farmaco.
Non è semplice (c'è tanta teoria da studiare) e, come se non bastasse, quello appena descritto non è l'unico approccio possibile.
Sergio grazie mille, i tuoi commenti e anche quelli di tommik sono molto apprezzati.
Non ti ho risposto prima perché da qualche giorno mi sono ritirato da Internet e da qualsiasi mezzo di comunicazione. Mi sono messo a capo chino sui libri come un monaco a studiare Statistica e Fisica Tecnica.
Come ha giustamente detto CLaudio Nine, la materia è molto più complicata del previsto.
Pensavo di aver terminato con l'inferenza....è invece è saltata fuori l'inferenza bayesiana. 
Sergio ma questi 4 punti riguardano l'inferenza statistica classica giusto?
In quale punto l'inferenza bayesiana è differente?
"Sergio":
1) assumi che il fenomeno d'interesse abbia una certa distribuzione di probabilità; ad esempio, nel lancio di una moneta assumi che si tratti di una distribuzione bernoulliana; formalmente, definisci il modello probabilistico $\{\chi, f_X(x;\theta), \Theta\}$ dove, nel caso di una bernoulliana:
-- $\chi$ è insieme dei valori che la v.a. può assumere, $\chi=\{0,1\}$;
-- $f_X(x;\theta)$ è la distribuzione di probabilità della variabile aleatoria, $\theta^x(1-\theta)^{1-x}$ (con $x in \chi$);
-- $\Theta$ è lo spazio dei parametri, l'insieme dei valori che il parametro può assumere, $\Theta=[0,1]$;
2) definisci il campione casuale come una $n$-upla di variabili aleatorie indipendenti e identicamente distribuite; ad esempio prendi i lanci di $n$ monete o $n$ lanci della stessa moneta e supponi di avere a che fare con $n$ variabili aleatorie bernoulliane; ottieni così il modello statistico che nel caso di $n$ lanci di una moneta è $\{\chi^n; f_n(x_n;\theta)=\prod_{i=1}^n f_X(x_i;\theta); \Theta\}$ dove:
-- $\chi^n=\{0,1\}\times\{0,1\}\times ... \times\{0,1\}=\{0,1\}^n$;
-- $f_n(x_n;\theta)=\prod_{i=1}^n f_X(x_i;\theta)=\prod_{i=1}^n \theta^x(1-\theta)^{1-x}=\theta^{\sum_i x_i}(1-\theta)^{n-\sum_i x_i}$;
-- $\Theta$ è ancora $[0,1]$;
3) definisci statistiche campionarie, che sono funzioni \(\chi^n \to \mathcal{T}\), con \(\mathcal{T}\subset\mathbb{R}^k, k\ge 1\); tra esse la media campionaria. Nel fare questo ragioni solo sulle $n$ variabili aleatorie;
4) guardi i valori osservati e cerchi di capire fino a che punto questi "si avvicinano" a quelli teorici, ad esempio quanto 4 teste in 10 lanci è coerente con la media campionaria se $\theta=0.5$ (moneta regolare).
Sergio ma questi 4 punti riguardano l'inferenza statistica classica giusto?
In quale punto l'inferenza bayesiana è differente?
Differente in tutto (io sono un bayesiano di formazione)
Qui, in evidenza nella prima pagina della stanza, trovi un mio riassunto sulla prova di ipotesi bayesiana con molti esempi che ho raccolto ed in parte rielaborato in diversi anni. Tali esempi possono essere ovviamente utilizzati anche per risolvere problemi di stima, sia puntuale che per intervallo.
Ne dovrei fare uno anche sulla stima ma sono argomenti che non interessano....ci dovrebbe essere anche qualche topic in proposito.
fammi sapere se sei interessato al problema
Qui, in evidenza nella prima pagina della stanza, trovi un mio riassunto sulla prova di ipotesi bayesiana con molti esempi che ho raccolto ed in parte rielaborato in diversi anni. Tali esempi possono essere ovviamente utilizzati anche per risolvere problemi di stima, sia puntuale che per intervallo.
Ne dovrei fare uno anche sulla stima ma sono argomenti che non interessano....ci dovrebbe essere anche qualche topic in proposito.
fammi sapere se sei interessato al problema
"tommik":
Differente in tutto (io sono un bayesiano di formazione)
Qui, in evidenza nella prima pagina della stanza, trovi un mio riassunto sulla prova di ipotesi bayesiana
Ne dovrei fare uno anche sulla stima ma sono argomenti che non interessano....ci dovrebbe essere anche qualche topic in proposito.
fammi sapere se sei interessato al problema
In tutto??? Mi era parso di capire che almeno il punto $1)$ fosse uguale!
P.s. Grazie mille per il riassunto tommik, lo divoro (sperando che non sia lui a divorare me).
"anonymous_58f0ac":
In tutto??? Mi era parso di capire che almeno il punto $1)$ fosse uguale!
Non è questione di "passaggi", anzi sotto alcune condizioni il risultato può essere lo stesso. E' proprio diversa la logica sottostante
qui un esercizio propedeutico che ho inventato proprio per far entrare l'utente nella logica bayesiana
qui un topic
qui una prima dispensina (davvero base, non esaustiva) che rende bene l'idea su come procedere
Prima di leggere il mio tutorial devi necessariamente avere un minimo (anche un po' più di un minimo) di basi. La logica bayesiana è completamente diversa da quella classica.
Se sei interessato sto preparando un bel topic sulle "osservazioni critiche" alle tecniche di Statistica Classica in contrapposizione a quella Bayesiana....ma per metterlo nero su bianco...anzi, nero su forum mi ci vuole del tempo...
Per iniziare a capire la differenza di logica fra Classico e Bayesiano dovresti almeno leggere anche l'altro tutorial, sulla ricerca dello stimatore ottimo in senso Classico...
qui un primo esempio sulla coerenza delle stime.
Vediamone un altro
Sia $X~N(theta;1)$. Il problema è quello di fare inferenza in modo Classico sul parametro ignoto $theta$, cioè sulla media della popolazione
Estraiamo un campione casuale $(X_1,X_2)$ e proponiamo i seguenti stimatori
$T_1=(X_1+X_2)/2$
$T_2=X_1$
Nella statistica classica la scelta tra due stimatori avviene generalmente confrontando l'Errore Quadratico Medio (EQM).
Vediamo subito che i due stimatori sono non distorti, essendo
$mathbb{E}[T_1]=1/2(theta+theta)=theta$
$mathbb{E}[T_2]=theta$
...e quindi per "misurare" la bontà dei due stimatori confrontiamo le loro varianze
$mathbb{V}[T_1]=1/4(1+1)=1/2$, $AA theta$
$mathbb{V}[T_2]=1$, $AA theta$
Quindi, ragionando in modo classico, $T_1$ è sempre preferito a $T_2$. Inoltre, per ragioni note e spiegate nei link precedenti, $T_1$ è lo stimatore ottimo in senso classico (la sua varianza raggiunge addirittura il limite inferiore di Cramér Rao)
Conclusione: scegliamo SEMPRE $T_1$ rispetto a $T_2$ (ed anche rispetto a qualunque altro stimatore non distorto) INDIPENDENTEMENTE da qualunque altra informazione in nostro possesso (è una scelta oggettiva).
Supponiamo ora di effettuare un esperimento e di aver ottenuto i seguenti dati
$x_1=4$
$x_2=1$
A questo punto le due stime saranno
$hat(T)_1=5/2$
$hat(T)_2=4$
Consideriamo ora l'errore quadratico (in funzione di $theta$) che si commette dopo aver osservato il dato sperimentale
1) $(theta-5/2)^2$
2) $(theta-4)^2$
Se disegnamo il grafico di tali errori, in funzione di $theta$
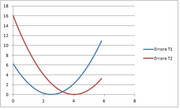
osserviamo che, a dispetto di tutta la teoria classica, se $theta>13/4$ (intersezione fra le due parabole) lo stimatore $T_2$ è preferito allo stimatore $T_1$.
Il fatto è dovuto che nella Statistica Classica si confronta la media degli errori indipendentemente da altre informazioni in nostro possesso
...vale quindi la pena di pensare ad un ragionamento induttivo coerente: ovvero usare il teorema di Bayes con tutto ciò che ne consegue.
"tommik":
qui un primo esempio sulla coerenza delle stime.
........
@tommik
In questi giorni sono stato meno presente sul forum perché un professore di un'altra materia ha pensato molto allegramente di mettere un esame parziale tra dieci giorni, e ce l'ha comunicato con un anticipo irrisorio.
Follie da quarantena. C'è da diventare matti.
grazie mille per tutto il materiale fornito.
E' oro perché il mio libro di testo è meno comprensibile sull'argomento inferenza e ho ancora vari dubbi, scontato dire quindi che sarà un piacere leggere.
Grazie ancora e buona serata a tommik, Sergio e CLaudio Nine!!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo