Probabilità condizionata e lancio di due dadi
Salve! Questo è il mio primo intervento nel forum, abbiate pietà se sbaglio con formule etc 
Penso di non aver capito bene il significato di probabilità condizionata: il mio dubbio nasce da questo esercizio
Ragionando intuitivamente mi sono detto: se un dado fa tre, le uniche possibilità per ottenere almeno 8 come somma sono che l'altro dado faccia 5 oppure 6, perciò ho 2 casi favorevoli su 3 casi possibili e la soluzione è \(\displaystyle \frac {2}{6} = \frac{1}{3} \).
Poi ho tirato fuori la definizione di probabilità condizionata per vedere se il ragionamento fosse giusto:
\(\displaystyle P(S>7|D=3) = \frac{P(S>7 \cap D = 3)}{P(D=3)} \)
che con la formula di Bayes diventa
\(\displaystyle \frac{P(S>7)P(D=3|S>7)}{P(S>7)P(D=3|S>7)+P(S\leq 7)P(D=3|S\leq 7)}\)
(con D ho indicato "uno dei due dadi")
Ho costruito una tabella che rappresenta lo spazio campionario
Dalla tabella vedo che il numeratore è pari a \(\displaystyle \frac{15}{36} \times \frac{4}{15} \) mentre il denominatore \(\displaystyle \frac{15}{36} \times \frac{4}{15} \times \frac{21}{36} \times \frac{7}{21}\), per un risultato finale di \(\displaystyle \frac{4}{11} \).
Il problema, a quanto vedo, è che all'inizio ho considerato uno spazio campionario che equivale alla sola colonna '3' della tabella, mentre applicando la teoria ho considerato l'intersezione della riga '3' e della colonna '3', quindi lo spazio campionario mi si "riduce di uno". Tuttavia, non riesco a capire come il significato della probabilità condizionata possa essere quello! In teoria, la conoscenza del risultato di un dado mi riduce l'incertezza al solo dado di cui non conosco il risultato!
Il professore mi ha fatto notare la differenza tra "ho sotto gli occhi un dado che ha fatto 3" e "so che uno dei due dadi (ma non so quale!) ha fatto 3", ma continuo a non afferrare bene in che modo ciò cambia la soluzione (mi ricorda in qualche modo il paradosso dei due bambini...).
Mi sto perdendo in un bicchier d'acqua? Grazie a chi risponderà e buona giornata

Penso di non aver capito bene il significato di probabilità condizionata: il mio dubbio nasce da questo esercizio
Si lanciano in maniera indipendente due dadi equilibrati a sei facce. Sapendo che uno di essi ha dato 3, qual è la probabilità che la somma dei due sia maggiore di 7?
Ragionando intuitivamente mi sono detto: se un dado fa tre, le uniche possibilità per ottenere almeno 8 come somma sono che l'altro dado faccia 5 oppure 6, perciò ho 2 casi favorevoli su 3 casi possibili e la soluzione è \(\displaystyle \frac {2}{6} = \frac{1}{3} \).
Poi ho tirato fuori la definizione di probabilità condizionata per vedere se il ragionamento fosse giusto:
\(\displaystyle P(S>7|D=3) = \frac{P(S>7 \cap D = 3)}{P(D=3)} \)
che con la formula di Bayes diventa
\(\displaystyle \frac{P(S>7)P(D=3|S>7)}{P(S>7)P(D=3|S>7)+P(S\leq 7)P(D=3|S\leq 7)}\)
(con D ho indicato "uno dei due dadi")
Ho costruito una tabella che rappresenta lo spazio campionario
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 2 |
| 4 | 5 | 6 | 7 | 8 | 3 | 4 |
| 6 | 7 | 8 | 9 | 4 | 5 | 6 |
| 8 | 9 | 10 | 5 | 6 | 7 | 8 |
| 10 | 11 | 6 | 7 | 8 | 9 | 10 |
Dalla tabella vedo che il numeratore è pari a \(\displaystyle \frac{15}{36} \times \frac{4}{15} \) mentre il denominatore \(\displaystyle \frac{15}{36} \times \frac{4}{15} \times \frac{21}{36} \times \frac{7}{21}\), per un risultato finale di \(\displaystyle \frac{4}{11} \).
Il problema, a quanto vedo, è che all'inizio ho considerato uno spazio campionario che equivale alla sola colonna '3' della tabella, mentre applicando la teoria ho considerato l'intersezione della riga '3' e della colonna '3', quindi lo spazio campionario mi si "riduce di uno". Tuttavia, non riesco a capire come il significato della probabilità condizionata possa essere quello! In teoria, la conoscenza del risultato di un dado mi riduce l'incertezza al solo dado di cui non conosco il risultato!
Il professore mi ha fatto notare la differenza tra "ho sotto gli occhi un dado che ha fatto 3" e "so che uno dei due dadi (ma non so quale!) ha fatto 3", ma continuo a non afferrare bene in che modo ciò cambia la soluzione (mi ricorda in qualche modo il paradosso dei due bambini...).
Mi sto perdendo in un bicchier d'acqua? Grazie a chi risponderà e buona giornata
Risposte
"PhilZara":
Salve! Questo è il mio primo intervento nel forum, abbiate pietà se sbaglio con formule etc


fossero tutti così i neoiscritti.....ora ci guardo
Se disegni lo spazio campionario nel modo corretto (le coppie nella tabella indicano le coppie di uscita $(i,j)$)
(click per ingrandire)
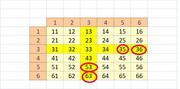
vedi che i casi favorevoli sono 4 su 11 possibili, quindi $4/11$
usando la definizione di probabilità condizionata trovi esattamente gli stessi casi favorevoli e possibili
"PhilZara":
Ragionando intuitivamente mi sono detto: se un dado fa tre, le uniche possibilità per ottenere almeno 8 come somma sono che l'altro dado faccia 5 oppure 6, perciò ho 2 casi favorevoli su 3 casi possibili e la soluzione è \(\displaystyle \frac {2}{6} = \frac{1}{3} \).
a parte che i casi sono 4: ${3;5}$; ${3;6}$;${5;3}$;${6;3}$
ma questi che hai calcolato sono i casi favorevoli...essendo tutti i 36 casi equiprobabili, per calcolare la probabilità condizionata devi rapportare i 4 casi trovati a tutti i casi possibili...che sono 11: 6 dove esce il 3 esce al primo lancio + 6 dove il 3 esce al secondo lancio meno 1 caso perché il $(3;3)$ lo devi contare una sola volta
(dalla teoria $P(AuuB)=P(A)+P(B)-P(A nnB)$)
Grazie! Quindi possiamo dire che il problema "filosofico" è la definizione di spazio campionario? Io stavo considerando valori singoli, mentre andrebbero prese in considerazione coppie non ordinate di valori in cui uno solo è noto, giusto? [ot]Probabilissimo sproloquio del principiante: mi torna in mente algebra... è come se stessi lavorando in una dimensione quando in realtà il mio spazio ne ha due? So che esistono i vettori aleatori ma non li abbiamo trattati nel corso e non ne so nulla, se avete qualche lettura consigliata ne farò buon uso  [/ot]
[/ot]
Tangenzialmente: se il problema avesse detto questo, la mia prima risposta sarebbe stata giusta?
Tangenzialmente: se il problema avesse detto questo, la mia prima risposta sarebbe stata giusta?
Si lancia un dado equilibrato a sei facce. Qual è la probabilità che sommando 3 al risultato si ottenga un valore maggiore di 7 ?
"PhilZara":
1) Io stavo considerando valori singoli, mentre andrebbero prese in considerazione coppie non ordinate di valori in cui uno solo è noto, giusto?
2) So che esistono i vettori aleatori ma non li abbiamo trattati nel corso e non ne so nulla, se avete qualche lettura consigliata ne farò buon uso
3) Tangenzialmente: se il problema avesse detto questo, la mia prima risposta sarebbe stata giusta?
Si lancia un dado equilibrato a sei facce. Qual è la probabilità che sommando 3 al risultato si ottenga un valore maggiore di 7 ?
1) sì, lo spazio campionario è formato da 36 coppie $Omega={(1;1),(1;2),...,(6;6)}$ ed è su questo che occorre ragionare. Dato che ogni evento è equiprobabile con probabilità $1/36$ è sufficiente contare gli eventi favorevoli e possibili.
2) sul forum ci sono centinaia e centinaia di esercizi e discussioni sull'argomento tutti svolti e commentati. Basta usare la funzione cerca
3) sì
Grazie! (c'è un bottone thanks su questo forum? Non sono riuscito a trovarlo quindi presumo di no ma se sbaglio dimmi pure  )
)


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo