$\mathbb(P)(U>1/2|T=t)$

[mobley]

Ho $T~ U(0,1)$ e $U|T~ U(0,T]$, da cui si ricava $f(t,u)=f_T(t)f_(U|T)(u|t)=1/t\mathbb(1)_({0,1})(t)\mathbb(1)_((0,T])(u)$. Allora ho

$\mathbb(P)(U>1/2)=\mathbb(P)(U>1/2|T=t)=\int_0^1[\int_(1/2)^t 1/tdu]dt$

ma nonostante sia sicuro dell'impostazione non ottengo una probabilità compresa tra 0 e 1. Cosa mi sfugge?

[Lo_zio_Tom]

ma perché invece di fare tutti sti ragionamenti farraginosi non ti fai un disegno???



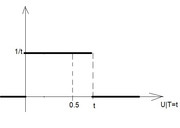
vedi subito che la probabilità cercata è l'area a destra di $1/2$

Ovvero

$(t-1/2)1/t=1-1/(2t)$

Questo ovviamente per $t in (1/2;1)$ e zero altrove....

easy peasy.....

[mobley]

"tommik":Ovvero $(t-1/2)1/t=1-1/(2t)$

Ma infatti integrando ottengo $\int_0^1 1/t(t-1/2)=\int_0^1 dt-1/2 \int_0^1 1/tdt$, tuttavia l'integrale non converge. E non capisco perchè.

[Lo_zio_Tom]

quella che ti ho calcolato è una probabilità (cioè è un numero) mica va integrata....

$P(U>1/2|T=t in (0;1))=[1-1/(2t)]mathbb{1}_([1/2;1))(t)$

ed al variare di $t$ trovi una probabilità in $[0;1/2)$

fine del problema.....

[mobley]

ok con il disegno, ci sono. non avrei mai capito che l'estremo inferiore di integrazione passava da zero a $1/2$. La domanda è: c'era un modo per capirlo anche senza disegno?

[Lo_zio_Tom]

"mobley":La domanda è: c'era un modo per capirlo anche senza disegno?

Ovviamente sì: dimenticandosi dei formulari e facendo funzionare i neuroni....ogni esercizio è a sé e si può risolvere solo ragionando (secondo me al tuo esame potrebbero farti portare anche le enciclopedie...ma se non ragioni sarà ben difficile risolvere i problemi)

Scusa eh....senza sapere nulla né di matematica né di statistica

La tua variabile condizionata va da $(0;t)$ e $t$ può essere fra zero e uno....se $t<1/2$ come può fare la tua condizionata ad essere maggiore di $1/2$????

Quindi vuoi la soluzione SENZA disegno....

La distribuzione condizionata $f(u|t)=1/t$ e quindi la sua funzione di sopravvivenza e $S_(U|T)(s)=1-s/t$

Il risultato cercato è evidentemente $S(1/2)=[1-1/(2t)]mathbb{1}_([1/2;1))(t)$

per le ovvie considerazioni precedenti

[Lo_zio_Tom]

"mobley":Allora ho

$\mathbb(P)(U>1/2)=\mathbb(P)(U>1/2|T=t)=\int_0^1[\int_(1/2)^t 1/tdu]dt$

ma nonostante sia sicuro dell'impostazione non ottengo una probabilità compresa tra 0 e 1. Cosa mi sfugge?

scusa ma lavorando leggo molto frettolosamente ciò che scrivi e quest'altra perla me l'ero persa....anche a causa del titolo ingannevole.

Devi calcolare la probabilità del titolo oppure $mathbb(P)[U>1/2]$??

non sono affatto la stessa cosa, una è una probabilità condizionata mentre l'altra è marginale.....se devi calcolare la probabilità marginale l'integrale che hai scritto [nonostante tu sia sicuro della correttezza della sua impostazione] è del tutto privo di senso (ed infatti nemmeno converge)...quello corretto è questo

$P[U>1/2]=int_(1/2)^1[int_(u)^1 1/t dt]du=(1-log2)/2~~ 0.1534$

se invece devi calcolare la probabilità condizionata del titolo...la spiegazione la trovi nei miei precedenti messaggi

Hint: se non riesci (e a quanto pare non riesci) a scrivere "di botto" l'integrale doppio puoi sempre procedere per gradi: hai la distribuzione di $T$ e quella di $U|T$....calcolati prima la distribuzione marginale $U$ e poi sarà immediato calcolare la probabiltà marginale (se quella è la probabilità richiesta dall'esercizio)