[interessante] sulle distribuzioni condizionate

[mobley]

Siano $X~ U(0,2)$ e $U|X=x~ N(x,1)$. Un punto dell'esercizio mi chiede di calcolare la probabilità che $U$ assuma valori positivi. Io ho fatto:

$\mathbb(P)(U>0)=\mathbb(P)(U>0|X=x)=1/(2\sqrt(2\pi))\int_0^2[\int_0^(+\infty)e^(-(u-x)^2)/2du]dx$

ma:
1) non so se è giusto;
2) anche se lo fosse non saprei come continuare perchè a quanto pare si tratta di una funzione non integrabile senza funzione degli errori. Cosa devo fare in questi casi (sempre che, ripeto, sia corretta l'impostazione)?

[Lo_zio_Tom]

Esattamente come ti ho spiegato precedentemente....

$mathbb{E}=mathbb{E}[mathbb{E}(U|X)]=mathbb{E}[X]=1$




Ora il risultato è immediato

[mobley]

"tommik":Esattamente come ti ho spiegato precedentemente

Il calcolo del valore atteso di $U$ era richiesto come primo punto dell'esercizio:

$E=E[E[U|X=x]]=1/2\int_0^2E[U|X=x]dx=1$

Tuttavia la mia domanda in questo caso è un'altra: come trasformo quell'integrale?

[Lo_zio_Tom]

ho risposto troppo frettolosamente....ma la soluzione, secondo me, è questa:

OBIETTIVO: trovare un accrocchio per evitare di risolvere quell'integrale

1) sappiamo che U è gaussiana, dato che al variare di $x in (0;2)$ si sposta solo la media.

2) dobbiamo quindi calcolare media e varianza di U in modo da avere una gaussiana ben definita per poter usare le tavole

3) la media di U l'abbiamo calcolata (anzi l'hai calcolata anche tu e viene 1)

4) la varianza di U?

Usiamo il teorema di scomposizione della varianza

$V(U)=E [V(U|X)]+V[E(U|X)]=E[1]+V[X]=1+4/12=4/3$

Ora sappiamo che, marginalmente, $U~N(1;4/3)$

e quindi $P[U>0]=1-Phi(-sqrt(3/4))=0.8068$

fammi sapere se è chiaro (sto lavorando e l'ho risolto al volo)

[mobley]

Anzitutto grazie per avermi confermato la correttezza della varianza (che era il secondo punto dell'esercizio).
Non ho capito come hai fatto a fare

$\int_(-x)^(+\infty)e^(-(u-x)^2/(2))du=1-\Phi(-\sqrt(3/4))$

[Lo_zio_Tom]

Ieri sera, con calma, non durante il lavoro, ho svolto l'esercizio in modo del tutto diverso da te e diverso anche da come ti ho spiegato nei precedenti messaggi.

Ecco come ho ragionato:

$(U|X)~N(x;1)$

$X~U(0;2)$

Definiamo la nuova variabile $Y=U-X$ ed osserviamo che, $AAx$ fissato, $(Y|X)~N(0;1)$.
Di conseguenza $Y$ e $X$ sono indipendenti. Ma allora $U=Y+X$ cioè $U$ è somma di una gaussiana std ed una uniforme (fra loro indipendenti).

Ora, senza ulteriori calcoli, si vede subito che media e varianza di $U$ sono, rispettivamente, la somma delle medie e varianze, cioè

$mathbb{E}=mathbb{E}[Y]+mathbb{E}[X]=0+1=1$ e

$mathbb{V}=mathbb{V}[Y]+mathbb{V}[X]=1+1/3=4/3$

Per terminare il ragionamento occorre dimostrare che, marginalmente, $U$ sia ancora normale.

Per provarlo occorrono parecchi conti....ecco un abbozzo

$F_U(u)=int_o^2 1/2dxint_(-oo)^(u-x)phi(y)dy=int_0^2 1/2Phi(u-x)dx$

derivando la F rispetto ad u otteniamo la densità di U che, visto come è fatta la funzione integranda, non dovrebbe essere molto diversa da una $phi_((mu; sigma^2))$, ovvero una gaussiana...i parametri li sappiamo già....problema risolto.

[strike]Avendo ora dimostrato[/strike] Essendo abbastanza confidente che marginalmente $U~N(1;4/3)$ per calcolare le probabilità di U, standardizzo ed uso le tavole della legge

$mathbb{P}[U>0]=1-Phi[(0-1)/sqrt(4/3)]=1-Phi(-sqrt(0.75))$

[mobley]

Ho guardato la tua soluzione e devo ammettere che rispetto alla mia è decisamente più elegante. In ogni caso, tornando a casa, ho pensato che magari si poteva sfruttare la ripartizione della Normale… Se infatti pongo $u-x=vrArr du=dv$, posso dire che $1/\sqrt(2\pi)\int_(-x)^(+\infty)e^(-v^2/(2))dv=1-F_X(-x)=1-\Phi(-x)$?
Lo chiedo a te, non ne sono sicuro… So solo che se $1/(2\pi)\int_(-\infty)^z e^(-z^2/2)dz=F_Z(z)$, potrei vedere quell'integrale come funzione inversa boh… Anche se a quel punto non saprei come usare le tavole della Normale standard

[Lo_zio_Tom]

Aggiornamento: Autocorrezioni, Precisazioni ed Approfondimenti

La densità della U non è propriamente una Gaussiana $N(1;4/3)$ come avevo immaginato ma si può approssimarla molto molto bene con tale densità.

Ho fatto i conti in modo analitico per caratterizzare la distribuzione marginale di U e questi sono i risultati:

$F_U(u)=int_(-oo)^(u-2)phi(y)dy underbrace(int_0^2 1/2dx)_(=1)+int_(u-2)^u phi(y)dyint_0^(u-y)1/2dx=$

$=Phi(u-2)+1/2int_(u-2)^u phi(y)(u-y)dy=Phi(u-2)+u/2int_(u-2)^u phi(y)dy-1/2int_(u-2)^u y phi(y)dy$

Quindi

$mathbb{P}[U>0]=1-F_U(0)=1-Phi(-2)+1/2int_(-2)^0 y phi(y)dy=$

$=1-Phi(-2)+1/(2sqrt(2pi))int_(-2)^0 ye^(-y^2/2)dy=1-0.02275+1/(2sqrt(2pi))[-e^(-y^2/2)]_(-2)^0=0.8048$


^^^^^^^^^^^^^^^^^^^ Fine dell'Esercizio ^^^^^^^^^^^^^^^^^^^^^^^^


Ma possiamo anche trovare la densità esatta di $U$ derivando la Funzione di Ripartizione (trattandosi di derivate di funzioni integrali metto anche tutti i passaggi)

$f_U(u)=phi(u-2)+1/2int_(u-2)^u phi(y)dy+u/2[phi(u)-phi(u-2)]-1/2uphi(u)+1/2(u-2)phi(u-2)=$

$=phi(u-2)+1/2int_(u-2)^u phi(y)dy+u/2phi(u)-u/2phi(u-2)-u/2phi(u)+u/2phi(u-2)-phi(u-2)$

Quindi (si elide quasi tutto....)

$f_U(u)=1/2int_(u-2)^u phi(y)dy$; $u in RR$

il grafico della $f(u)$ esatto, sovrapposto al grafico della densità $N(1;4/3)$ è rappresentato in figura

(click per ingrandire)


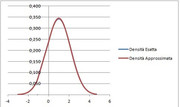
In conclusione, il risultato esatto di $80.48%$ non è molto dissimile dal risultato a cui ero pervenuto già inizialmente e senza molte pippe, ovvero che

$mathbb{P}[U>0]~~80.68%$