Esercizio probabilità congiunta
Buongiorno,
Ho provato a risolvere un esercizio sulla funzione di probabilità congiunta. Riporto il testo e i miei passaggi. Potreste dirmi se è giusto o se (molto probabile
) ho fatto qualche errore. Grazie!
TESTO
Sia $f_(xy)(x,y)=4xy*e^(-(x^2+y^2))$ per $x>=0, y>=0$ (0 altrove), la funzione congiunta di probabilità di due variabili $X$ e $Y$.
Calcolare:
1) la densità di probabilità di $X^2$
2) la densità di probabilità di $Z=sqrt(X^2+Y^2)$
SOLUZIONE
1) Dopo aver ricavato le densità di probabilità $f_x(x)$ e $f_y(y)$ e verificato che sono indipendenti ho effettuato una trasformazione di variabile:
$f_x(x)=2x*e^(-x^2)$ per $x>=0$ (0 altrove)
$W=X^2$
$f(x)=g(y(x))*|y'(x)|$
da cui si ricava $g_w(w)=e^(-w)$ per $w>=0$ (0 altrove)
2) Poichè ho difficoltà a fare ragionamenti di tipo geometrico, ho effettuato anche qui una trasformazione passando alle variabili X e Y alle variabili:
${(Z=sqrt(X^2+Y^2)),(W=X^2):}$
Quindi facendo la trasformazione $f(x,y)=g(z,w)*|DET(J)|$ si ottiene:
$g_z(z)=2z*e^(-z^2)$ per $z>=0$ (0 altrove)
Ho provato a risolvere un esercizio sulla funzione di probabilità congiunta. Riporto il testo e i miei passaggi. Potreste dirmi se è giusto o se (molto probabile
) ho fatto qualche errore. Grazie! TESTO
Sia $f_(xy)(x,y)=4xy*e^(-(x^2+y^2))$ per $x>=0, y>=0$ (0 altrove), la funzione congiunta di probabilità di due variabili $X$ e $Y$.
Calcolare:
1) la densità di probabilità di $X^2$
2) la densità di probabilità di $Z=sqrt(X^2+Y^2)$
SOLUZIONE
1) Dopo aver ricavato le densità di probabilità $f_x(x)$ e $f_y(y)$ e verificato che sono indipendenti ho effettuato una trasformazione di variabile:
$f_x(x)=2x*e^(-x^2)$ per $x>=0$ (0 altrove)
$W=X^2$
$f(x)=g(y(x))*|y'(x)|$
da cui si ricava $g_w(w)=e^(-w)$ per $w>=0$ (0 altrove)
2) Poichè ho difficoltà a fare ragionamenti di tipo geometrico, ho effettuato anche qui una trasformazione passando alle variabili X e Y alle variabili:
${(Z=sqrt(X^2+Y^2)),(W=X^2):}$
Quindi facendo la trasformazione $f(x,y)=g(z,w)*|DET(J)|$ si ottiene:
$g_z(z)=2z*e^(-z^2)$ per $z>=0$ (0 altrove)
Risposte
"lordstark90":
Quindi facendo la trasformazione $f(x,y)=g(z,w)*|DET(J)|$ si ottiene:
$g_z(z)=2z*e^(-z^2)$ per $z>=0$ (0 altrove)
Grave....grave errore! peccato, davvero peccato per questo scivolone finale, con tutto l'esercizio perfetto.
La funzione che hai trovato (e che ho citato) è la congiunta $(ZW)$, non la marginale Z
$f_(ZW)=2ze^(-z^2)$
ne sei convinto o no?
Le marginali risultano, integrando tale densità congiunta sul supporto dell'altra variabile (con questo metodo le trovi subito tutte e due le marginali):
$f_W=e^(-w)$ ; $w>=0$ (corretto, è una esponenziale negativa)
$f_Z=2z^3e^(-z^2)$; $z>=0$
Perché? Quali sono gli estremi corretti di integrazione? Per capirlo è necessario prima capire quale sia il supporto congiunto del vettore $(Z,W)$ che, ovviamente, NON è tutto il primo quadrante....
Oppure puoi usare un
Metodo alternativo
Per quanto riguarda $W=X^2$ ok, va bene come hai fatto.
Per quanto riguarda la trasformazione $Z=sqrt(X^2+Y^2)$ ti suggerisco questo medoto pressoché immediato. Trasforma il vettore aletorio in coordinate polari, ottenendo subito
$f_(P Theta)(rho,theta)=4rho^3e^(-rho^2)costheta sentheta=2costheta sen theta xx 2rho ^3e^(-rho^2)$
dove si vede subito che la congiunta è il prodotto di due densità indipendenti, una dell'angolo ($theta in [0; pi/2] $)e l'altra del raggio
...essendo il raggio proprio $rho=sqrt(X^2+Y^2)$ hai la distribuzione cercata.
Grazie mille anche per il metodo alternativo!
Immaginavo di aver sbagliato la funzione finale. Non comparendo la variabile w ho dato frettolosamente per scontato che fosse la $g_z(z)$, ma in effetti non ha senso. Quindi per ottenere $g_z(z)$ bisogna fare così:
$g_z(z)=\int_{0}^{z^2-y^2} 2z*e^(-z^2) dw$
Giusto?
Immaginavo di aver sbagliato la funzione finale. Non comparendo la variabile w ho dato frettolosamente per scontato che fosse la $g_z(z)$, ma in effetti non ha senso. Quindi per ottenere $g_z(z)$ bisogna fare così:
$g_z(z)=\int_{0}^{z^2-y^2} 2z*e^(-z^2) dw$
Giusto?
di male in peggio (ci sono molti esercizi sul forum, anche più articolati, che ti invito a studiarti per bene)
Partendo dall'ottimo sistema che hai scritto
${{: ( W=X^2 ),( Z=sqrt(X^2+Y^2) ) :}rarr{{: ( X=sqrt(W) ),( Y=sqrt(Z^2-W) ) :}$
appare subito evidente che deve essere anche $z^2-w>=0 rarr z>=sqrt(w)$
e quindi
$f_W=int_(sqrt(w))^(+oo)f_(ZW)dz$
$f_Z=int_(0)^(z^2)f_(ZW)dw$
Dato che il dominio congiunto è questo
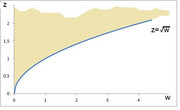
fine.
Partendo dall'ottimo sistema che hai scritto
${{: ( W=X^2 ),( Z=sqrt(X^2+Y^2) ) :}rarr{{: ( X=sqrt(W) ),( Y=sqrt(Z^2-W) ) :}$
appare subito evidente che deve essere anche $z^2-w>=0 rarr z>=sqrt(w)$
e quindi
$f_W=int_(sqrt(w))^(+oo)f_(ZW)dz$
$f_Z=int_(0)^(z^2)f_(ZW)dw$
Dato che il dominio congiunto è questo
fine.
Ok perfetto grazie mille ho rimescolato un pò di cose Andrò sicuramente a vedere un pò di esercizi nel forum.
Invece cambiando approccio è giusta una risoluzione di questo tipo o c'è qualche errore concettuale?
$f_(xy)(x,y)=4xy*e^-(x^2+y^2)$
$Z=sqrt(X^2+Y^2)$
$F_z(z)=P(Z<=z)=P(X<=sqrt(z^2-Y^2))=int_{0}^{z} int_{0}^{sqrt(z^2-Y^2)} f(x,y) dx dy$
Risolvendo si dovrebbe ottenere $F_z(z)=-e^(-z^2)*(z^2+1)+1$ da cui poi ottenere:
$f_z(z)=F'_z(z)=2z^3*e^(-z^2)$
Giusto?
Andrò sicuramente a vedere un pò di esercizi nel forum.Invece cambiando approccio è giusta una risoluzione di questo tipo o c'è qualche errore concettuale?
$f_(xy)(x,y)=4xy*e^-(x^2+y^2)$
$Z=sqrt(X^2+Y^2)$
$F_z(z)=P(Z<=z)=P(X<=sqrt(z^2-Y^2))=int_{0}^{z} int_{0}^{sqrt(z^2-Y^2)} f(x,y) dx dy$
Risolvendo si dovrebbe ottenere $F_z(z)=-e^(-z^2)*(z^2+1)+1$ da cui poi ottenere:
$f_z(z)=F'_z(z)=2z^3*e^(-z^2)$
Giusto?
giusto. Macchinoso e brutto, secondo me.
Ecco qui un esercizio fresco fresco quasi tutto risolto.... tanto l'utente che lo ha postato non si farà più né vedere né sentire..se lo guardi e ti può essere utile sono contento....almeno non ho buttato del tempo
Ecco qui un esercizio fresco fresco quasi tutto risolto.... tanto l'utente che lo ha postato non si farà più né vedere né sentire..se lo guardi e ti può essere utile sono contento....almeno non ho buttato del tempo
Si molto macchinoso e non è nemmeno detto che si riescano a risolvere facilmente gli integrali. Ma almeno se so che è giusto posso provare più metodi per verificare se i risultati sono uguali. 
Grazie mille davvero per il tempo dedicato. Guarderò un pò di materiale in giro per il forum e l'esercizio che mi hai mandato che sarà sicuramente di aiuto per farmi capire meglio
Grazie mille davvero per il tempo dedicato. Guarderò un pò di materiale in giro per il forum e l'esercizio che mi hai mandato che sarà sicuramente di aiuto per farmi capire meglio
Accedi a tutti gli appunti
Tutor AI: studia meglio e in meno tempo