Dubbio sul paradosso di bertrand

[ulissess]

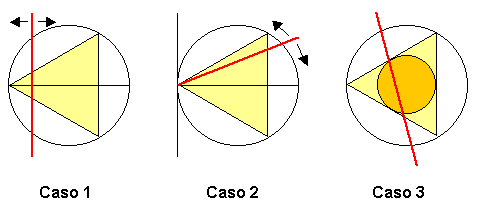
ciao ragazzi, rileggendo le soluzioni di questo paradosso, non riesco a comprendere il caso 3 nella foto.. non riesco a capire come fa a dire che se il punto mediano della corda cade dentro la circonferenza di raggio r/2 allora è sicuro che la corda è più lunga di $r*sqrt(3)$ sicuramente è una questione di geometria ma non mi viene niente in mente. ringrazio per le eventuali risposte

[K.Lomax]

Fissiamo un punto [tex]P[/tex] all'interno della circonferenza di centro [tex]O[/tex] e raggio [tex]R[/tex]e consideriamo quella corda per cui esso risulti proprio il punto medio della stessa. Indichiamo con [tex]Q[/tex] uno dei due punti di intersezione della corda con tale circonferenza e costruiamo un altro cerchio tale che il punto medio sia tangente a questo (in pratica, guardando la figura del caso 3 della tua figura, fai in modo che la linea rossa sia tangente al cerchio arancione). E' facile vedere che si forma un triangolo rettangolo [tex]O\hat P Q[/tex] (Th: una tangente in un qualsiasi punto di una circonferenza forma un angolo di 90° con il raggio della circoferenza). Di conseguenza, si ha:

[tex]PQ^2=OQ^2-OP^2[/tex]

Ma, per ipotesi, [tex]PQ=\frac{c}{2}[/tex] (metà corda), [tex]OQ=R[/tex] e [tex]OP=r[/tex]. Dunque:

[tex]\frac{c^2}{4}=R^2-r^2[/tex]

[tex]c=2\sqrt{R^2-r^2}[/tex]

Affinché essa sia maggiore di [tex]R\sqrt{3[/tex] deve aversi

[tex]2\sqrt{R^2-r^2}>R\sqrt{3}[/tex]

ovvero

[tex]r^2<\frac{R^2}{4}[/tex]

[tex]r<\frac{R}{2}[/tex] cvd