Dubbi esercizio distribuzione
Buongiorno per favore qualcuno potrebbe dirmi dove sbaglio in quest'esercizio?
La distribuzione dei pesi dei neonati di una popolazione `e di tipo gaussiano con media
$µ=3Kg$. e scarto quadratico medio pari a $500$ gr. Calcolare su un gruppo di 900 neonati quanti ce ne
aspettiamo con peso inferiore a 2 Kg.
Calcolo $z=(2-3)/(1/2)$
$z=-2$
= controllo il valore corrispondente sulla tavola di Gauss fuori dall'intervallo $mi-u×sigma$
$0,0456$
Calcolo $1-0.0456$ = $0.97$ circa ma il risultato è $17,5$ e $2,5 %$
Credo di sbagliare a scegliere la tabella non ho capito quando bisogna calcolare 1- il valore trovato sulla tabella oppure quando bisogna scrivere 1/2 - tale valore
potreste darmi qualche consiglio per favore?
Grazie mille
La distribuzione dei pesi dei neonati di una popolazione `e di tipo gaussiano con media
$µ=3Kg$. e scarto quadratico medio pari a $500$ gr. Calcolare su un gruppo di 900 neonati quanti ce ne
aspettiamo con peso inferiore a 2 Kg.
Calcolo $z=(2-3)/(1/2)$
$z=-2$
= controllo il valore corrispondente sulla tavola di Gauss fuori dall'intervallo $mi-u×sigma$
$0,0456$
Calcolo $1-0.0456$ = $0.97$ circa ma il risultato è $17,5$ e $2,5 %$
Credo di sbagliare a scegliere la tabella non ho capito quando bisogna calcolare 1- il valore trovato sulla tabella oppure quando bisogna scrivere 1/2 - tale valore
potreste darmi qualche consiglio per favore?
Grazie mille
Risposte
Ciao, dipende se le tue tavole rappresentano i quantili di coda destra o sinistra.
Comunque, per capire come usarle, disegnati la Gaussiana e prendi un punto a piacere.
Vedrai, per simmetria, le relazioni che sussistono tra $Phi(x)$ e $Phi(-x)$.
Per esempio, se la tua tavola indica i quantili di coda sinistra (la funzione di ripartizione quindi), e prendi $x=-1$, l'area da $-oo$ a $-1$ sarà uguale a quella da $1$ a $+oo$, che sarà quindi uguale a $1-Phi(1)$, perché sai che l'area su tutto $RR$ è $1$.
Comunque, per capire come usarle, disegnati la Gaussiana e prendi un punto a piacere.
Vedrai, per simmetria, le relazioni che sussistono tra $Phi(x)$ e $Phi(-x)$.
Per esempio, se la tua tavola indica i quantili di coda sinistra (la funzione di ripartizione quindi), e prendi $x=-1$, l'area da $-oo$ a $-1$ sarà uguale a quella da $1$ a $+oo$, che sarà quindi uguale a $1-Phi(1)$, perché sai che l'area su tutto $RR$ è $1$.
Grazie mille ho due tavole per qiesto sono in confusione ma quindi èsbagliato calcolare $z$ come ho fatto io?
Scusatemi ancora potreste per favore dirmi cortesemente gli errori dei miei calcoli?
$2=mu+usigma$
$u=(2-3)/(0,5)$
$-2$
Controllo questo valore sulla tabella corrisponde a $0.0456$
Quindi sottraggo $1-0.46=0.54$
continuo a svolgere l'esercizio ma non capisco perché i conti non mi tornano. Perché deve venire $17.5$?
Vi ringrazio tanto
$2=mu+usigma$
$u=(2-3)/(0,5)$
$-2$
Controllo questo valore sulla tabella corrisponde a $0.0456$
Quindi sottraggo $1-0.46=0.54$
continuo a svolgere l'esercizio ma non capisco perché i conti non mi tornano. Perché deve venire $17.5$?
Vi ringrazio tanto
Forse mi sto complicando da sola i conti
Non è che basterebbe effettuare
$3-0,5$?
Non è che basterebbe effettuare
$3-0,5$?
Ciao, in questo caso non serve fare il calcolo esplicito; quando si ha a che fare con curve gaussiane si può dimostrare che il 95% circa dei casi cadono tra $mu-2sigma$ e $mu+2sigma$, questo lo puoi vedere meglio se ti fai un grafico:
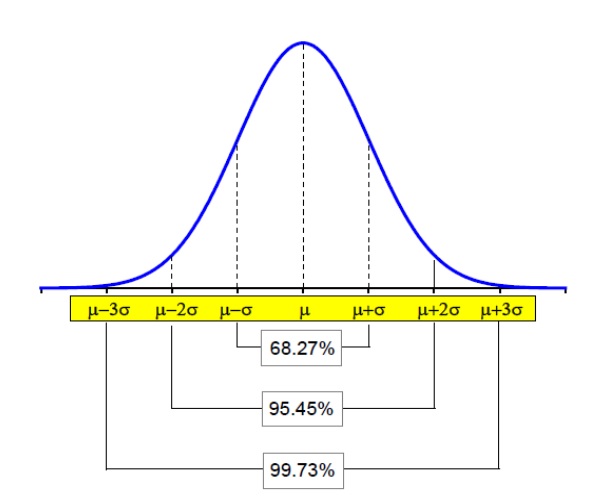
Siccome cerchiamo i valori minori di 2 (cioè $mu-2sigma$), si tratta di un semplice problema geometrico:
considerando quanto detto prima, il 5% dei casi cadrà fuori da $[mu-2sigma$,$mu+2sigma]$, e, per simmetria, il 2.5% starà prima di 2, l'altro 2.5% dopo 4.
Quindi basta calcolare il 2.5% di 900, che però fa 22.5, non 17.5;
Spero di non aver sbagliato qualcosa, mi sono avvicinato a questi problemi da poco. Confido in chi è più esperto per eventuali conferme o correzioni. Ciao

Siccome cerchiamo i valori minori di 2 (cioè $mu-2sigma$), si tratta di un semplice problema geometrico:
considerando quanto detto prima, il 5% dei casi cadrà fuori da $[mu-2sigma$,$mu+2sigma]$, e, per simmetria, il 2.5% starà prima di 2, l'altro 2.5% dopo 4.
Quindi basta calcolare il 2.5% di 900, che però fa 22.5, non 17.5;
Spero di non aver sbagliato qualcosa, mi sono avvicinato a questi problemi da poco. Confido in chi è più esperto per eventuali conferme o correzioni. Ciao
Grazie mille
perché per simmetria 2.5 starà prima di 2 e 2.5 dopo di 4 perché la funzione è simmetrica giusto?
Mi confondo troppo mi potreste dare qualche consiglio sull'uso delle tabelle ? Io sul libro ho una sola tabella ma ho notato che nei testi di esame si usano due tabelle ma con quale criterio si sceglie di usare una tabella al posto di un'altra?
Grazie mille e scusate l'ignoranza
perché per simmetria 2.5 starà prima di 2 e 2.5 dopo di 4 perché la funzione è simmetrica giusto?
Mi confondo troppo mi potreste dare qualche consiglio sull'uso delle tabelle ? Io sul libro ho una sola tabella ma ho notato che nei testi di esame si usano due tabelle ma con quale criterio si sceglie di usare una tabella al posto di un'altra?
Grazie mille e scusate l'ignoranza
Si, per simmetria. Per capire meglio rileggiti il primo messaggio che ho scritto.
Per quanto riguarda le tabelle è solo una questione di convenzione. In genere alcune riportano $Phi(t)$, altre $1-Phi(t)$, anche questo era scritto nel primo messaggio; comunque ogni tavola è dotata di un'intestazione che specifica i dati esposti, o indicando l’espressione analitica della funzione tabulata o, più semplicemente, mettendo il grafico della funzione di densità in cui viene annerita la regione di probabilità di interesse.
Per quanto riguarda le tabelle è solo una questione di convenzione. In genere alcune riportano $Phi(t)$, altre $1-Phi(t)$, anche questo era scritto nel primo messaggio; comunque ogni tavola è dotata di un'intestazione che specifica i dati esposti, o indicando l’espressione analitica della funzione tabulata o, più semplicemente, mettendo il grafico della funzione di densità in cui viene annerita la regione di probabilità di interesse.
Grazie mille volendo riportare i calcoli richiesti sul testo d'esame $z$ lo devo scrivere come ho fatto sopra? Grazie infinitee mi scuso per il disturbo
Se vuoi farti il calcolo esplicito devi trovarti $P(X<=2) = P((X-mu)/sigma<=-2)=1-Phi(2) ~~0.023$, cioè circa il 2.3%; poi ti trovi il 2.3% di 900, che è circa 21. Non so se non mi viene 17, come nel libro, per errori di approssimazione, o se sto sbagliando qualcosa; ma credo la prima. Ciao
Grazie mille davvero gentile


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo