Distribuzioni marginali
Ho due variabili casuali congiunte $X$ e $Y$ che sono distribuite come un triangolo che ha vertici (0,0) (1,0) (0,1). Devo calcolare le distribuzioni marginali e la funzione di ditribuzione di $Z=X+Y$.
Io ho pensato che $fxy$ è l'area del triangolo, quindi $fxy=1/2$, da qui per ricavare le marginali uso gli integrali.
Trovo la retta $y=-x+1$.
Per ricavare $fx$ integro $fxy$ tra $0$ e $-x+1$, per ricavare $fy$ la integro invece fra $0$ e $-y+1$.
Facendo il prodotto delle due marginali trovo che non sono indipendenti.
Per trovare la funzione di ripartizione di $Z$ faccio un integrale doppio di $fxy$ con $x$ che varia da $0$ a $z$ e $y$ che varia da $0$ a $z-x$. Per trovare da ddp faccio poi la derivata di $Fz$.
Vorrei sapere se questo procedimento è giusto, visto che non ho le soluzioni.
Io ho pensato che $fxy$ è l'area del triangolo, quindi $fxy=1/2$, da qui per ricavare le marginali uso gli integrali.
Trovo la retta $y=-x+1$.
Per ricavare $fx$ integro $fxy$ tra $0$ e $-x+1$, per ricavare $fy$ la integro invece fra $0$ e $-y+1$.
Facendo il prodotto delle due marginali trovo che non sono indipendenti.
Per trovare la funzione di ripartizione di $Z$ faccio un integrale doppio di $fxy$ con $x$ che varia da $0$ a $z$ e $y$ che varia da $0$ a $z-x$. Per trovare da ddp faccio poi la derivata di $Fz$.
Vorrei sapere se questo procedimento è giusto, visto che non ho le soluzioni.
Risposte
"robytb4e":
Ho due variabili casuali congiunte $X$ e $Y$ che sono distribuite come un triangolo ...
già distribuite come.....come cosa? magari sono uniformi.....in tal caso la distribuzione congiunta sarà il reciproco dell'area...ovvero $f_(XY)(x,y)=2$ sul triangolo in oggetto e zero altrove....il resto sembra ok.
La densità non è richiesta, è richiesta solo la funzione di distribuzione.
PS: sarebbe più interessante sul triangolo di vertici
$(0;0)$;$(1;0)$;$(1;1)$
No non parla di distribuzione uniforme. Il testo dice "Si considerino due v.c. congiunte X,Y" e poi c'è la figura del triangolo che ho spiegato.
Riguardo al fatto dell'indipendenza, se il prodotto delle due marginali è uguale alla congiunta allora sono indipendenti, ma vale anche il viceversa? Nel senso, visto che il prodotto delle due marginali è diverso dalla congiunta posso dire che non sono indipendenti?
Riguardo al fatto dell'indipendenza, se il prodotto delle due marginali è uguale alla congiunta allora sono indipendenti, ma vale anche il viceversa? Nel senso, visto che il prodotto delle due marginali è diverso dalla congiunta posso dire che non sono indipendenti?
Se non dice che il vettore è distribuito uniformemente sul triangolo non lo puoi risolvere: per poter fare i conti hai necessariamente bisogno di avere la distribuzione congiunta; se essa è uniforme calcoli la densità come reciproco dell'area altrimenti il testo ti deve dare lui la distribuzione (quindi è una palese dimenticanza del testo)
Per l'indipendenza la condizione da te usata è Necessaria e Sufficiente (quindi la risposta è Sì, vale anche il viceversa) ma qui è inutile:
Condizione necessaria per l'indipendenza è che il dominio sia rettangolare....qui è un triangolo quindi niente indipendenza
Per l'indipendenza la condizione da te usata è Necessaria e Sufficiente (quindi la risposta è Sì, vale anche il viceversa) ma qui è inutile:
Condizione necessaria per l'indipendenza è che il dominio sia rettangolare....qui è un triangolo quindi niente indipendenza
Probabilmente sarà un errore del testo, ma a questo punto penso che siano uniformi. Quindi considero $fxy=2$ e risolvo così?
[ot]Se i triangolo fosse di vertici (0,1) (1,0) (1,1) cambierebbero gli estremi di integrazione, giusto? Per la $x$ diventerebbero $-x+1$ e $1$, per la $y$ diventerebbero $-y+1$ e $1$[/ot]
[ot]Se i triangolo fosse di vertici (0,1) (1,0) (1,1) cambierebbero gli estremi di integrazione, giusto? Per la $x$ diventerebbero $-x+1$ e $1$, per la $y$ diventerebbero $-y+1$ e $1$[/ot]
I triangolo "interessante" a cui mi riferisco è questo
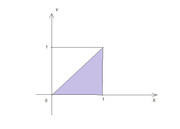
e gli estremi di integrazione sono ovviamente riferiti alla variabile $Z=X+Y$
Prova a farlo perché è interessante....è simile al caso che hai postato l'altro giorno ma più interessante perché si risolve con un po' di ragionamento ma senza immani calcoli


e gli estremi di integrazione sono ovviamente riferiti alla variabile $Z=X+Y$
Prova a farlo perché è interessante....è simile al caso che hai postato l'altro giorno ma più interessante perché si risolve con un po' di ragionamento ma senza immani calcoli
Grazie infinite, gentilissimo come sempre!


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo