Densità di $W=(X+Y)/2$

[mobley]

Non ne vengo a capo:

date $X,Z$ i.i.d.$~ U(1,a)$, qual'è la distribuzione di $W=(X+Y)/2$?

Non capisco perchè sia sbagliato imporre $\mathbb(P)(X<=2w-z)=\int_(1)^(a)[\int_(1)^(2w-z)(1)/((a-1)^2)dx]dz$.

[Lo_zio_Tom]

"mobley":

date $X,Z$ i.i.d.$~ U(1,a)$, qual'è la distribuzione di $W=(X+Y)/2$?

In Primis: stai attento quando riporti i dati.....sarà $X,Y$ uniformi i.i.d......oppure $W=(X+Z)/2$

In Secundis: stai attento all'ortografia: qual'è (con l'apostrofo) non si può guardare....

Tornando alla soluzione.....parto dal presupposto che siano $X,Y$ le marginali indipendenti.

l'integrale non è solo sbagliato....è proprio una cosa senza alcun senso logico (ho provato e riprovato a dargli un senso statistico ma non ci sono riuscito, sembra un integrale scritto a caso), oltre che inutile. Infatti, dato che la distribuzione è uniforme, l'integrale non serve a nulla....si risolve tutto con il calcolo di semplici aree geometriche.

La CDF in questione viene così:


$F_W(w)={{: ( 0 ,;w<1 ),( (2(w-1)^2)/(a-1)^2 , ;1<=w<(a+1)/2 ),( 1-(2(a-w)^2)/(a-1)^2 , ;(a+1)/2<=w=a ) :}$

EDIT: dato che so già che la mia risposta non ti soddisferà allora ho (mio malgrado) provato a risolverlo con gli integrali (metodo totalmente inutile[nota]quando ero io uno studente il prof valutava anche l'ordine logico / formale con cui si affrontavano i problemi e risovere un esercizio così con l'uso degli integrali doppi, anche se in modo corretto, non avrebbe strappato un voto maggiore di 19/30. Sì forse il prof era uno stronXo però in questo modo ho imparato a ragionare...[/nota])

$F_W(w)=1/(a-1)^2 int_1^(2w-1)dxint_1^(2w-x)dy=...=(2(w-1)^2)/(a-1)^2$

che combacia con l'altro risultato (che ho calcolato come area di un triangolo, ovvero facendo semplicemente $("base "xx" altezza")/2$); questo però solo quando $w in [1;(a+1)/2)$ dopo ovviamente la solfa cambia....serve calcolare l'area di un altro triangolo oppure impostare un altro integrale (che non sto a scrivere)

Come si fa?

Come sempre con TUTTI gli integrali doppi

1) si studia la base di analisi

2) si fa il disegno del dominio

3) si vede come cambia il dominio al variare della variabile di interesse (in questo caso $w$)

4) si opera integrando nel modo più economico (con questi esempi ci sono sempre diversi modi di scrivere l'integrale corretto)

EDIT2: in modo da non aver segreti (ed anche perché la mia risposta possa essere utile a tutti) ecco come ho calcolato la prima parte della CDF (ho fatto il grafico a mano con paint di windows quindi le proporzioni fanno pene)

(click per ingrandire)


basta fare l'area del triangolino viola moltiplicata per la densità congiunta, ovvero

$1/(a-1)^2 xx (2w-1-1)^2/2=(2(w-1)^2)/(a-1)^2$


per l'ultima parte non ho fatto altro che fare uno meno l'area del triangolino residuo....quindi un calcolo del tutto simile....tempo di risoluzione max 5 minuti, senza tirare in ballo integrali doppi, calcoli complicati con conseguenti errori di calcolo, perdite di tempo ecc ecc

[mobley]

Messaggio a dir poco ILLUMINANTE

Solo due cose non mi sono chiare.
1) Gli intervallini di $w$. Nel calcolare l'area del triangolino viola hai messo come intervallo $1<=w<(a+1)/2$ ad indicare giustamente (tramite l'estremo superiore) che ci troviamo nella metà bassa del quadrato spezzato in due dalla retta $z=a+1$. E ok.
Poi però, nel calcolare l'area del quadrato restante come $(1-$triangolino viola$)$, metti come intervallo $(a+1)/2<=w 2) La densità di $W$. Perchè se relativamente al triangolino si ottiene $(4(w-1))/((a-1)^2)$, calcolando $(\partial)/(\partial w)(1-(2(w-1)^2)/((a-1)^2))$ si ottiene una densità negativa?

[Lo_zio_Tom]

"tommik":
per l'ultima parte non ho fatto altro che fare uno meno l'area del triangolino residuo....

ovviamente per "uno meno il triangolino residuo" si intende l'area viola, ovvero

$F=1-(2(a-w)^2)/(a-1)^2$

cioè 1 meno l'area del triangolino residuo (quello bianco in alto a destra[nota]che, anche se disegnato da cane, ha i cateti uguali[/nota]) moltiplicata per la densità congiunta $f(x,y)$.

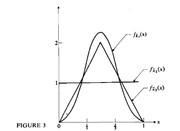
Derivando la F che ho scritto qui[nota]$F_W(w)={{: ( 0 ,;w<1 ),( (2(w-1)^2)/(a-1)^2 , ;1<=w<(a+1)/2 ),( 1-(2(a-w)^2)/(a-1)^2 , ;(a+1)/2<=w=a ) :}$[/nota] si ottiene (come è naturale) una densità triangolare. Aldilà di alcuni parametri, è lo stesso identico esempio del calcolo della distribuzione di $Z=X+Y$ con $X,Y$ uniformi su $[0;1]$ che hai fatto più volte con almeno 3 metodi differenti (metodo della funzione di ripartizione, convoluzione e metodo generale, quello con il calcolo dello jacobiano).

Utilizzando la convoluzione e le proprietà dell'induzione si trova anche la densità generica di $Z=1/n sum_(i=1)^n X_i$. La formula chiusa per tale densità la trovi sui principali libri di Statistica elementare (libri seri, ovviamente)





...te capì adess??

Nel tuo messaggio hai scritto una serie di errori ed inesattezze evidenti che non ho voglia di stare a correggere.