Densità di probabilità di X1/X2 dove X1~U(0,1) e X2~U(1,2)
Salve ragazzi, so che è banale ma volevo chiedervi una mano per questo esercizio.
"Sia X1 una variabile aleatoria con distribuzione Unif(0,1) e X2 con distribuzione Unif(1,2), determinare la densit´a di probabilit´a di V = |X1|/|X2|."
Online ho trovato una risoluzione (che allego in foto) per un esercizio quasi uguale ma volevo sapere se c'era un metodo alternativo.
Grazie a chiunque mi risponderà!

"Sia X1 una variabile aleatoria con distribuzione Unif(0,1) e X2 con distribuzione Unif(1,2), determinare la densit´a di probabilit´a di V = |X1|/|X2|."
Online ho trovato una risoluzione (che allego in foto) per un esercizio quasi uguale ma volevo sapere se c'era un metodo alternativo.
Grazie a chiunque mi risponderà!

Risposte
1) non è consentito inserire le immagini al posto del testo o della soluzione di un problema (per stavolta ok ma fai attenzione)
2) nel tuo esercizio non hai scritto che le variabili devono essere indipendenti. E' necessario che lo siano o che vi siano altre info.
3) il metodo descritto nell'immagine postata è il metodo "tradizionale" che usa il teorema fondamentale di trasformazione, va bene ma puoi tranquillamente fare come hai fatto (anzi come ho fatto) nel tuo precedente post: disegni il dominio e ci fai passare in mezzo la funzione di trasformazione.
Quindi ricapitoliamo, per comodità di chi legge:
$F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[X<=Yz]=mathbb{P}[Y>X/z]$
solita storia.....a conti fatti (3 secondi e mezzo, non di più) trovi che
$F_Z(z)={{: ( 0 , ;z<0 ),( 3/2z , ;0<=z<1/2 ),( 1-(1-z)^2/(2z) , ;1/2<=z<1 ),( 1 , ;z>=1 ) :}$
...più altri 3 secondi per derivare la F e trovare la densità richiesta.
2) nel tuo esercizio non hai scritto che le variabili devono essere indipendenti. E' necessario che lo siano o che vi siano altre info.
3) il metodo descritto nell'immagine postata è il metodo "tradizionale" che usa il teorema fondamentale di trasformazione, va bene ma puoi tranquillamente fare come hai fatto (anzi come ho fatto) nel tuo precedente post: disegni il dominio e ci fai passare in mezzo la funzione di trasformazione.
Quindi ricapitoliamo, per comodità di chi legge:
$X~ U(0;1)$; $Y~ U(1;2)$; $X,Y$ indipendenti, trovare la densità di $Z=X/Y$
$F_Z(z)=mathbb{P}[X/Y<=z]=mathbb{P}[X<=Yz]=mathbb{P}[Y>X/z]$
solita storia.....a conti fatti (3 secondi e mezzo, non di più) trovi che
$F_Z(z)={{: ( 0 , ;z<0 ),( 3/2z , ;0<=z<1/2 ),( 1-(1-z)^2/(2z) , ;1/2<=z<1 ),( 1 , ;z>=1 ) :}$
...più altri 3 secondi per derivare la F e trovare la densità richiesta.
Ok perdonami per la foto, non lo sapevo.
Grazie ancora comunque, ho l' esame tra pochi giorni e mi hai aiutato davvero molto!
Buonaserata
Grazie ancora comunque, ho l' esame tra pochi giorni e mi hai aiutato davvero molto!
Buonaserata
Il metodo descritto con la tua immagine va saputo, non è un optional[nota]a seconda dell'esercizio può essere più conveniente uno o l'altro.[/nota].
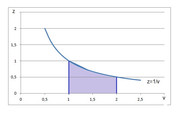
Ad esempio, se l'esercizio chiedesse di trovare la densità congiunta $f_(X/Y,Y)(z,v)$ non avresti alternative. Nel caso in esame verrebbe $f_(ZV)(z,v)=v mathbb{1}_((0;1))(zv)mathbb{1}_((1;2))(v)$ ovvero in questo dominio
Prova quindi a risolvere i due problemi con entrambi i metodi, è un ottimo esercizio per padroneggiare l'argomento. Il fatto di avere già le soluzioni dovrebbe aiutarti.
Ad esempio, se l'esercizio chiedesse di trovare la densità congiunta $f_(X/Y,Y)(z,v)$ non avresti alternative. Nel caso in esame verrebbe $f_(ZV)(z,v)=v mathbb{1}_((0;1))(zv)mathbb{1}_((1;2))(v)$ ovvero in questo dominio

Prova quindi a risolvere i due problemi con entrambi i metodi, è un ottimo esercizio per padroneggiare l'argomento. Il fatto di avere già le soluzioni dovrebbe aiutarti.
Sto cercando di trovare la densità di $ x/y $ con il metodo della variabile ausiliaria. Dove $ x=x1 $ e $ y=x2 $ Ho imposto $ u=x/y $ e $ y=v $ , ho isolato le variabili $ y $ e $ x $ e il determinante dello jacobiano mi viene $ detJ=v $ , ottengo quindi che $ f(u,v)=v*1(v)*(u) $ dove $ 1<= v<= 2, 0<= u<= 1/v $ . Integro quindi su $ v $ : $ f(u)=int_(1)^(2) v dv $ per $ 0<= u<= 0.5 $ e $ f(v)=int_(1/u)^(2) v dv $ per $ 0.5<= u<= 1 $ . Purtroppo non mi combaciano i risultati e sono un po' incerto sgli estremi di integrazione e come vanno scelti
all'inizio è facile confondersi; è per questo che ti ho fatto anche il disegno del dominio (ho indicato con $z$ ciò che tu indichi con $u$)
Se devi trovare la densità di $u$ devi integrare in $v$ la congiunta.
Il primo tratto è corretto:
$f_U(u)=int_1^2 v dv=3/2$ per $0
Il secondo viene così
$f_U(u)=int_1^(1/u) v dv=1/(2u^2)-1/2$ per $1/2
Come si vede bene dal disegno

Prova a derivare la Funzione di ripartizione che ti ho indicato precedentemente e vedi che tutto torna.
Se devi trovare la densità di $u$ devi integrare in $v$ la congiunta.
Il primo tratto è corretto:
$f_U(u)=int_1^2 v dv=3/2$ per $0
Il secondo viene così
$f_U(u)=int_1^(1/u) v dv=1/(2u^2)-1/2$ per $1/2
Come si vede bene dal disegno

Prova a derivare la Funzione di ripartizione che ti ho indicato precedentemente e vedi che tutto torna.


 Accedi a tutti gli appunti
Accedi a tutti gli appunti
 Tutor AI: studia meglio e in meno tempo
Tutor AI: studia meglio e in meno tempo